浙江省温州市2021-2022学年九年级上学期数学期末试卷
试卷更新日期:2022-02-14 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1. 下列四个交通标志中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线 的顶点坐标为( )A、(-4,-5) B、(-4,5) C、(4,-5) D、(4,5)3. 如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针落在数字1,2,3,4所示区域内可能性最大的是( )
2. 抛物线 的顶点坐标为( )A、(-4,-5) B、(-4,5) C、(4,-5) D、(4,5)3. 如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针落在数字1,2,3,4所示区域内可能性最大的是( ) A、1号 B、2号 C、3号 D、4号4. 若 ,则下列等式成立的是( )A、 B、 C、 D、5. 如图, 是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F.若 ,则 的值为( )
A、1号 B、2号 C、3号 D、4号4. 若 ,则下列等式成立的是( )A、 B、 C、 D、5. 如图, 是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F.若 ,则 的值为( ) A、 B、 C、 D、6. 如图,在⊙O中,半径OC⊥AB于点D.已知OC=5,OD=4,则弦AB的长为( )
A、 B、 C、 D、6. 如图,在⊙O中,半径OC⊥AB于点D.已知OC=5,OD=4,则弦AB的长为( ) A、3 B、4 C、5 D、67. 如图,A,B,C是⊙O上的点,满足CA平分∠OCB.若∠OAC=25°,则∠AOB的度数为( )
A、3 B、4 C、5 D、67. 如图,A,B,C是⊙O上的点,满足CA平分∠OCB.若∠OAC=25°,则∠AOB的度数为( ) A、40° B、50° C、55° D、60°8. 如图,在 中,点 在BC边上,连结DE并延长交AB的延长线于点 .若 ,则 与 的周长之比为( )
A、40° B、50° C、55° D、60°8. 如图,在 中,点 在BC边上,连结DE并延长交AB的延长线于点 .若 ,则 与 的周长之比为( ) A、1:3 B、3:7 C、4:7 D、3:49. 二次函数 的部分图象如图所示,当 时,函数值 的取值范围是( )
A、1:3 B、3:7 C、4:7 D、3:49. 二次函数 的部分图象如图所示,当 时,函数值 的取值范围是( ) A、 B、 C、 D、10. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、 B、 C、 D、10. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )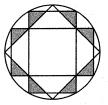 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题(本题有8小题,每小题3分,共24分)
-
11. 抛物线 与 轴的交点坐标是.12. 若线段 ,则a,b的比例中项线段为.13. 如图,点 在半圆 上,BC是直径, .若 ,则BC的长为.
 14. 若圆的半径为3cm,圆周角为25°,则这个圆周角所对的弧长为cm.15. 明明家过年时包了50个饺子,其中有5个饺子包有幸运果.明明一家人连续吃了10个饺子都没有吃到幸运果,那么明明在剩余的饺子中任意挑选一个饺子,正好是包有幸运果饺子的概率是.16. 如图,在△ABC中,点D在AC上,∠ABD=∠C.若AB=2AD=4,则CD的长是.
14. 若圆的半径为3cm,圆周角为25°,则这个圆周角所对的弧长为cm.15. 明明家过年时包了50个饺子,其中有5个饺子包有幸运果.明明一家人连续吃了10个饺子都没有吃到幸运果,那么明明在剩余的饺子中任意挑选一个饺子,正好是包有幸运果饺子的概率是.16. 如图,在△ABC中,点D在AC上,∠ABD=∠C.若AB=2AD=4,则CD的长是. 17. 二次函数y=ax2+bx+c的部分对应值列表如下:
17. 二次函数y=ax2+bx+c的部分对应值列表如下:x
…
-3
0
1
3
5
…
y
…
7
-8
-9
-5
7
…
则一元二次方程a(2x+1)2+b(2x+1)+c=-5的解为.
18. 某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB上地面,AB=120 cm,Р是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40 cm,斜拉杆AE可绕点A旋转,AE= CP.若∠APE=30°,则BP=cm;伞展开长 PD==300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为cm.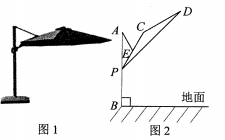
三、解答题(本题有6小题,共46分)
-
19. 小聪参加一个幸运挑战活动,规则是:在一个箱子里有3个白球和1个红
球,它们除颜色外其余都相同,现从箱子里摸出1个球,不放回,记下颜色,再摸出1个球,若两次摸出球的颜色相同,则挑战成功.
(1)、请用列表法或树状图法,表示出所有可能的结果.(2)、求小聪挑战成功的概率.20. 如图,在6×6的正方形网格中,点A,B,C均在格点上,请按要求作图. (1)、在图1中画一个格点△ADE,使△ADC∽△ABC.(2)、在图2中画一条格点线段BP,交AC于点Q,使CQ=2AQ.21. 已知二次函数y=ax2+bx (a≠0)的图象经过点A(2,4),B(4,0) .
(1)、在图1中画一个格点△ADE,使△ADC∽△ABC.(2)、在图2中画一条格点线段BP,交AC于点Q,使CQ=2AQ.21. 已知二次函数y=ax2+bx (a≠0)的图象经过点A(2,4),B(4,0) . (1)、求这个二次函数的表达式.(2)、将x轴上的点P先向上平移3n (n>0)个单位得点P,再向左平移2n个单位得点2 , 若点P1 , P2均在该二次函数图象上,求n的值.22. 如图,四边形ABCD 内接于半圆О,AB是直径,C是 的中点,延长AD,BC交于点E.
(1)、求这个二次函数的表达式.(2)、将x轴上的点P先向上平移3n (n>0)个单位得点P,再向左平移2n个单位得点2 , 若点P1 , P2均在该二次函数图象上,求n的值.22. 如图,四边形ABCD 内接于半圆О,AB是直径,C是 的中点,延长AD,BC交于点E. (1)、求证:CE=CD.(2)、若AB=5,BC= ,求AD的长.23. 某校需要订购中考专用的某款跳绳α条和排球2a个,经调查发现,该款跳
(1)、求证:CE=CD.(2)、若AB=5,BC= ,求AD的长.23. 某校需要订购中考专用的某款跳绳α条和排球2a个,经调查发现,该款跳绳、排球各商家均标价为50元/条,40元/个,现有3家商店在做促销活动如下表:
商店
促销活动
甲
库存充裕,全场9折.
乙
库存充裕,按套数(含1条跳绳和1个排球)优惠:30套及以内,每套85元;超过30套,每增加1套,所有套数每套优惠0.5元,但降幅不超过15元.
丙
仅库存排球55个,排球每满5个送1个.
(1)、若仅在一家商店购买,请用含a的代数式分别表示甲、乙两店的费用,填写下表.a
商店0<a≤30
30<a≤60
a>60
甲
乙
(2)、当a=60时,请你通过计算设计一种购买方案,使得总费用不超过6220元.24. 如图,在Rt△ABC中,∠CAB=90°,AC=3,AB=4,AD⊥BC于点D,射线CE平行AB交AD的延长线于点E,Р是射线CE上一点(在点E的右侧),连结AP交BC于点F.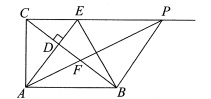
 (1)、求证: .(2)、若 ,求 的值.(3)、以PF为直径的圆经过 中的某一个顶点时,求所有满足条件的EP的长.
(1)、求证: .(2)、若 ,求 的值.(3)、以PF为直径的圆经过 中的某一个顶点时,求所有满足条件的EP的长.