浙江省瑞安市2021-2022学年九年级上学期第一次学业水平适应性测试数学试卷

试卷更新日期：2022-02-14 类型：月考试卷

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分．)

1. 若 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、2

查看试题解析
2. 已知⊙O的半径为5，点P在⊙O外，则OP的长可能是（）

A、3 B、4 C、5 D、6

查看试题解析
3. 将抛物线 $y = x^{2}$ 向上平移1个单位，所得抛物线的表达式为（）

A、 $y = x^{2} + 1$ B、 $y = x^{2} - 1$ C、 $y = {(x + 1)}^{2}$ D、 $y = {(x - 1)}^{2}$

查看试题解析
4. 某班从4名男生和2名女生中任选1人参加“我的数学故事”演讲比赛，则选中女生的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
5. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形， $O$ 为位似中心，位似比为2：3.若 $A B = 4$ ，则DE的长为（）

A、6 B、8 C、9 D、10

查看试题解析
6. 如图AB是半圆 $O$ 的直径C，D是半圆上的两点，若 $∠ C = 125^{°}$ ，则 $∠ A B D$ 的度数是（）

A、 $25^{°}$ B、 $30^{°}$ C、 $35^{°}$ D、 $40^{°}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A C B = 90^{°} ， ∠ A = 60^{°} ， A C = 2$ ，将 $△ A B C$ 绕点 $C$ 顺时针旋转得到 $△ D E C$ ，使点 $A$ 的对应点 $D$ 恰好落在边AB上，连结BE，则BE的长为（）

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
8. 为了解决楼房之间的采光问题，我市有关部门规定：两幢楼房之间的最小距离要使中午12时不能遮光.如图，旧楼的一楼窗台高1米，现计划在旧楼右侧50米处再建一幢新楼.若我市冬天中午12时太阳照射的光线与水平线的夹角最小为α度，则新楼最高可建（ )

A、 $50 \tan α$ 米 B、 $\frac{50}{\tan α}$ 米 C、 $(50 \tan α + 1)$ 米 D、 $(\frac{50}{\tan α} + 1)$ 米

查看试题解析

9. 下表是若干组二次函数

y = x^{2} - 5 x + c

的自变量

x

与函数值

y

的对应值：

x	…	1.3	1.4	1.5	1.6	1.7	…
y	…	0.36	0.13	-0.08	-0.27	-0.44	…

那么方程 $x^{2} - 5 x + c = 0$ 的一个近似根(精确到0.1)是（）

A、3.4 B、3.5 C、3.6 D、3.7

查看试题解析

10. 如图，在 $△ A B C$ 中， $∠ A C B = 90^{°}$ ，分别以AB，AC，BC为边向外作正方形.连结CD，若 $\sin ∠ B C D = \frac{3}{5}$ ，则 $\tan ∠ C D B$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{4}$ C、 $\frac{7}{10}$ D、 $\frac{9}{13}$

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分)

11. 正六边形每个内角的度数为度.

查看试题解析
12. 一个不透明的袋中装有红、白两种颜色的球共20个，除颜色外其余均相同．小丹通过多次摸球试验后发现，其中摸到红球的频率稳定在25%左右，则袋中红球大约有个.

查看试题解析
13. 已知一个扇形的半径为6，圆心角为150°，则这个扇形的弧长为.

查看试题解析
14. 如图，AB为 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $E ， C D = 10 ， B E = 3$ ，则AE长为.

查看试题解析
15. 已知二次函数 $y = a x^{2} + 2 a x - 3 a$ (其中 $x$ 是自变量)图象与 $x$ 轴交于A，B两点，当 $x ⩾ 0$ 时， $y$ 随 $x$ 的增大而减小. $P$ 为抛物线上一点，且横坐标为 $m$ ，当 $- 2 ⩽ m ⩽ 2$ 时， $△ A B P$ 面积的最大值为8，则 $a$ 的值为.

查看试题解析
16. 如图1，一个菱形可以分割成八个全等的等边三角形，按图2所示的方式(不重叠无缝隙摆放在矩形纸片ABCD内，顶点E，F，G，H，M，N均恰好落在矩形ABCD的边上，若菱形的边长为4，则FG的长为， BC的长为.

查看试题解析

三、解答题（本题有8小题，共80分．)

17.

(1)、计算： $\cos^{2} 45^{°} + \sin 30^{°} \cdot \tan 45^{°}$ .

(2)、求二次函数 $y = \frac{1}{2} x^{2} + 2 x + 1$ 图象的顶点坐标.

查看试题解析
18. 有三张正面分别标有1，2，3的不透明卡片，它们除数字外其余都相同，现将它们背面朝上洗均匀.

(1)、随机抽取一张卡片，求卡片上的数字是偶数的概率.

(2)、随机抽取一张卡片，记下数字后放回洗均匀，再随机抽取一张卡片，请用列表或画
树状图的方法，求两次抽取的卡片上的数字之和等于5的概率.

查看试题解析
19. 如图，在 $△ A B C$ 中，D，E分别是AB，AC上的点， $∠ A D E = ∠ C ， A F$ 平分 $∠ B A C$ 交DE于点 $G$ ，交BC于点 $F$ .

(1)、求证： $\frac{A D}{A C} = \frac{A G}{A F}$ .

(2)、若点 $G$ 是 $△ A B C$ 的重心， $A E = 6$ ，求AB的长.

查看试题解析
20. 如图，在6×6的正方形网格中，每个小正方形的边长都为1，点A，B，C均在格点上.请按要求在网格中画图，所画图形的顶点均需在格点上.

(1)、在图1中以线段AB为边画一个△ABD，使其与△ABC相似，但不全等.

(2)、在图2中画一个△EFG，使其与△ABC相似，且面积为8.

查看试题解析
21. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3$ 经过点 $A (- 1 ， 0) ， B (5 ， 0)$ .

(1)、求抛物线的表达式.

(2)、过点 $C (0 ， m)$ 作直线 $l / / x$ 轴交拋物线于点 $P$ ， $Q$ (点 $P$ 在点 $Q$ 的左侧)，若 $Q C = 3 P C$ ，求 $m$ 的值.

查看试题解析
22. 如图， $△ A B C$ 内接于 $⊙ O ， A B = A C ， D$ 为 $\overset{⌢}{A C}$ 上一点，过点 $B$ 作 $B E / / A D$ 交DC延长线于点 $E$ ，连结BD.

(1)、求证： $∠ A B D = ∠ C B E$

(2)、若AD=12，cosE= $\frac{1}{3}$ ，求CE的长.

查看试题解析
23. 马屿红糖闻名遐迩，是瑞安市名特产，某经销商将红糖加工成礼盒装出售，
经调查统计发现，礼盒装每天的销售量y(盒)与每盒售价x(元/盒)之间有如下关系：y=-10x+600．已知红糖礼盒装每盒的成本为20元，设该经销商每天所获利润为w(元).

(1)、求w关于x的函数表达式.

(2)、若礼盒装每天销量不少于220盒，且每盒利润不低于7元，求经销商每天获得的最大利润.

查看试题解析
24. 如图，在△ABC中，∠C=90°，D为边BC上一点，DE⊥AB于点E，以DE为直径的OO分别交线段BD，AD于点F，G，连结EF、EG.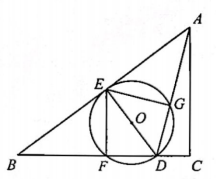

(1)、求证：△DEF∽△ABC.

(2)、若AC=6，BC=8，当DG与四边形DGEF其它三边中的一边相等时，求所有满足条件的BD的长.

(3)、当AC=BC时，连结OC交AD于点H，记△DOH的面积为S₁ ， △ACH的面积为S₂ ，若OC∥EG.则 $\frac{S_{1}}{S_{2}}$ 的值为.(在横线上直接写出答案)

查看试题解析