河北省唐山市2022届高三上学期数学期末考试试卷
试卷更新日期:2022-02-14 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、[1,2] B、[1,3] C、[0,2] D、[0,3]2. 函数为奇函数,为偶函数,在公共定义域内,下列结论一定正确的是( )A、为奇函数 B、为偶函数 C、为奇函数 D、为偶函数3. 为了得到函数的图像,只需把函数的图像( )A、向左平移个单位 B、向右平移个单位 C、向左平移个单位 D、向右移个单位4. 六名志愿者到北京、延庆、张家口三个赛区参加活动,若每个赛区两名志愿者,则安排方式共有( )A、15种 B、90种 C、540种 D、720种5. 传说古希腊毕达哥拉斯派的数学家经常在沙滩上面画点或用小石子表示数.他们将 , 称为三角形数;将 , 称为正方形数.现从小于100的三角形数中,随机抽取一个数,则这个数是正方形数的概率为( )A、 B、 C、 D、6. 已知抛物线C:的焦点为F, , 是C上两点,若 , 则( )A、 B、 C、 D、27. 设 , , , 则( )A、 B、 C、 D、8. 已知圆柱的侧面积为2π,其外接球的表面积为S,则S的最小值为( )A、3π B、4π C、6π D、9π
二、多选题
-
9. 已知复数(且),是z的共扼复数,则下列命题中的真命题是( )A、 B、 C、 D、10. 圆M:关于直线对称,记点 , 下列结论正确的是( )A、点P的轨迹方程为 B、以PM为直径的圆过定点 C、的最小值为6 D、若直线PA与圆M切于点A,则11. 为排查新型冠状病毒肺炎患者,需要进行核酸检测.现有两种检测方式:(1)逐份检测:(2)混合检测:将其中k份核酸分别取样混合在一起检测,若检测结果为阴性,则这k份核酸全为阴性,因而这k份核酸只要检测一次就够了,如果检测结果为阳性,为了明确这k份核酸样本究竟哪几份为阳性,就需要对这k份核酸再逐份检测,此时,这k份核酸的检测次数总共为次.假设在接受检测的核酸样本中,每份样本的检测结果是阴性还是阳性都是独立的,并且每份样本是阳性的概率都为 , 若 , 运用概率统计的知识判断下列哪些p值能使得混合检测方式优于逐份检测方式.(参考数据:)( )A、0.4 B、0.3 C、0.2 D、0.112. 如图,四边形ABCD是边长为2的正方形,E为AB的中点,将沿DE所在的直线翻折,使A与重合,得到四棱锥 , 则在翻折的过程中( )
 A、 B、存在某个位置,使得 C、存在某个位置,使得 D、存在某个位置,使四棱锥的体积为1
A、 B、存在某个位置,使得 C、存在某个位置,使得 D、存在某个位置,使四棱锥的体积为1三、填空题
-
13. 等差数列的公差为2,若 , , 成等比数列,则 .14. 中,为的中点, , , 则 .15. 已知圆锥的母线长为2,其侧面展开图是一个半圆,则该圆锥的体积为 .16. 已知函数 , 分别是的极大值点与极小值点,若且 , 则 .
四、解答题
-
17. 记的内角A,B,C的对边分别为a,b,c,已知 .(1)、求角C;(2)、求的取值范围.18. 已知是数列的前n项和, , 且 .(1)、证明:为常数列;(2)、若 , 求数列的前n项和 .19. 四棱锥的底面是矩形, , 侧面底面OBCD.
 (1)、求证:底面OBCD;(2)、若 , 二面角的大小为120°,求四棱锥的体积.20. 某统计部门依据《中国统计年鉴——2017》提供的数据,对我国1997-2016年的国内生产总值(GDP)进行统计研究,作出了两张散点图:图1表示1997-2016年我国的国内生产总值(GDP),图2表示2007-2016年我国的国内生产总值(GDP).
(1)、求证:底面OBCD;(2)、若 , 二面角的大小为120°,求四棱锥的体积.20. 某统计部门依据《中国统计年鉴——2017》提供的数据,对我国1997-2016年的国内生产总值(GDP)进行统计研究,作出了两张散点图:图1表示1997-2016年我国的国内生产总值(GDP),图2表示2007-2016年我国的国内生产总值(GDP).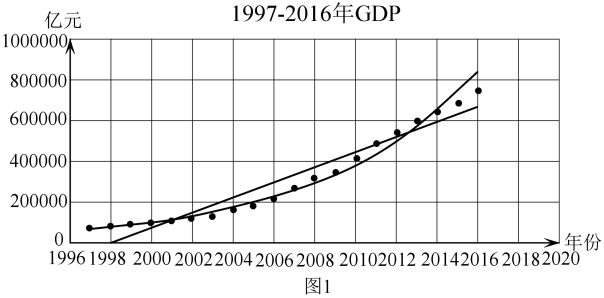
 (1)、用表示第i张图中的年份与GDP的线性相关系数, , 依据散点图的特征分别写出的结果;(2)、分别用线性回归模型和指数回归模型对两张散点图进行回归拟合,分别计算出统计数据——相关指数的数值,部分结果如下表所示:
(1)、用表示第i张图中的年份与GDP的线性相关系数, , 依据散点图的特征分别写出的结果;(2)、分别用线性回归模型和指数回归模型对两张散点图进行回归拟合,分别计算出统计数据——相关指数的数值,部分结果如下表所示:年份
1997-2016
2007-2016
线性回归模型
0.9306
指数回归模型
0.9899
0.978
①将上表中的数据补充完整(结果保留3位小数,直接写在答题卡上);
②若估计2017年的GDP,结合数据说明采用哪张图中的哪种回归模型会更精准一些?若按此回归模型来估计,2020年的GDP能否突破100万亿元?事实上,2020年的GDP刚好突破了100万亿元,估计与事实是否吻合?结合散点图解释说明.