河北省邯郸市2021-2022学年高一上学期数学期末考试试卷
试卷更新日期:2022-02-14 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、{4} B、{2} C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 下列函数中,既是偶函数又在上单调递增的是( )A、 B、 C、 D、5. 若 , , , 则( )A、 B、 C、 D、6. 如图是来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC、直角边AB、AC,已知以直角边AC、AB为直径的半圆的面积之比为 , 记 , 则的值为( )
 A、-1 B、-2 C、0 D、17. 函数的图象大致是( )A、
A、-1 B、-2 C、0 D、17. 函数的图象大致是( )A、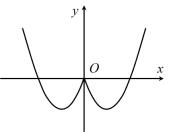 B、
B、 C、
C、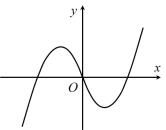 D、
D、 8. 设函数关于的方程有7个不同的实数根,则实数的取值范围是( )A、 B、 C、 D、
8. 设函数关于的方程有7个不同的实数根,则实数的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、10. 将函数的图象向左平移个单位后得到函数的图象,则( )A、与的最小正周期都是 B、的图象关于点对称. C、的图象关于直线对称 D、在区间上单调递增11. 已知函数则( )A、的单调递减区间为 B、的解集为 C、若有三个不同的根,则实数 D、存在最大值3和最小值212. 已知函数 , 且 , 则( )A、 B、为非奇非偶函数 C、函数的值域为 D、不等式的解集为
三、填空题
-
13. 已知扇形的半径为8,面积为20,则圆心角的弧度数为.14. 计算:.15. 已知( , 为常实数),若 , 则.16. 若正实数 , 满足 , 则的最小值为.
四、解答题
-
17. 设集合 , .(1)、求;(2)、求.18. 已知 , .(1)、求的值;(2)、求的值.19. 已知函数(且).(1)、判断的奇偶性并予以证明;(2)、若一元二次不等式的解集为 , 求不等式的解集.20. 目前全球新冠疫情严重,核酸检测结果成为是否感染新型冠状病毒的重要依据,某核酸检测机构,为了快速及时地进行核酸检测,花费36万元购进核酸检测设备.若该设备预计从第1个月到第n个月的检测费用和设备维护费用总计为万元,该设备每月检测收入为20万元.(1)、该设备投入使用后,从第几个月开始盈利?(即总收入减去成本及所有支出费用之差为正值);(2)、若该设备使用若干月后,处理方案有两种:①月平均盈利达到最大值时,以20万元的价格卖出;②盈利总额达到最大值时,以16万元的价格卖出.哪一种方案较为合算?请说明理由.
