吉林省吉林市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，已知线段n与挡板另一侧的四条线段a，b，c，d中的一条在同一条直线上，请借助直尺判断该线段是（）

A、a B、b C、c D、d

查看试题解析
2. 如果向东走15米记作+15米，那么向西走20米记作（）

A、+5米 B、+20米 C、-5米 D、-20米

查看试题解析
3. 如图，注射器中的新型冠状病毒疫苗的含量约为 $0.5 m l$ ，则关于近似数0.5的精确度说法正确的是（）

A、精确到个位 B、精确到十分位 C、精确到百分位 D、精确到千分位

查看试题解析
4. 一个骰子相对两面的点数之和为7，它的展开图如图所示，下列判断正确的是（）

A、A代表 B、B代表 C、B代表 D、C代表

查看试题解析
5. 已知等式2a＝3b﹣1，则下列等式中不成立的是（）

A、2a＋1＝3b B、2a﹣1＝3b﹣2 C、2ac＝3bc﹣c D、a＝ $\frac{3}{2}$ b﹣1

查看试题解析
6. 北京与巴黎的时差为7小时，例如：北京时间13：00，同一时刻的巴黎时间是早上6：00，笑笑和霏霏分别在北京和巴黎，她们相约在各自当地时间13：00～22：00之间选择一个时刻开始通话，这个时刻可以是北京时间（）

A、14：00 B、16：00 C、21：00 D、23：00

查看试题解析

二、填空题

7. 2021年党中央首次颁发“光荣在党50年”纪念章，约7100000名党员获此纪念章，数7100000用科学记数法表示为．

查看试题解析
8. 比较两个数的大小：﹣ $\frac{2}{3}$ ﹣ $\frac{3}{2}$ （填“＞”“＜”或“＝”）．

查看试题解析
9. 计算：42°36′＋35°43′＝．

查看试题解析
10. 若单项式2x^my⁵和﹣x²yⁿ是同类项，则n﹣3m的值为．

查看试题解析
11. 如图所示，建筑工人砌墙时，经常在两个墙角的位置分别插一根小桩，然后拉一条直的参照线，可以这样做的数学道理．

查看试题解析
12. 如图，已知点C在点O的东北方向，点D在点O的北偏西20°方向，那么∠COD为度．

查看试题解析
13. 我国古代著作《增删算法统宗》中记载了一首古算诗：“林下牧童闹如簇，不知人数不知竹每人六竿多十四，每人八竿恰齐足”其大意是：“牧童们在树下拿着竹竿高兴地玩耍，不知与多少人和竹竿每人6竿，多14竿；每人8竿，恰好用完”若设有牧童x人，根据题意，可列方程为．

查看试题解析
14. “双减”政策实施以后，吉林市全面开展了中小学生课后服务工作．目前，吉林市市区大部分学校七、八年级的学生每天下午6：30放学，这时时针与分针所成的角为．

查看试题解析
15. 如图，在平面内有A，B，C三点．请画直线AC，线段BC，射线AB，数数看，此时图中共有个钝角．

查看试题解析

三、解答题

16. 计算： $- 15 - (- 3) + (- 8)$ ．

查看试题解析
17. 计算：|﹣4|÷ $\frac{1}{2}$ ×（﹣3）²

查看试题解析
18. 解方程：3（x＋1）＝5x﹣1

查看试题解析
19. 先化简，再求值： $3 (2 a b^{2} - a^{2} b) - 6 (a b^{2} - \frac{1}{3} a^{2} b)$ ，其中a＝ $\frac{1}{2}$ ， b＝﹣1

查看试题解析
20. 如图，点C是线段AB的中点，点D是线段BC上的一点，点E是线段CD的中点，AB＝20，BD＝4

(1)、求线段CD的长；

(2)、求线段BE的长．

查看试题解析
21. 随着短视频软件的普及，许多人利用各种直播平台做电商，小李也将自己家果园的苹果梨在某直播平台进行销售，经过一段时间的销售，小李发现每天能销售100kg左右的苹果梨，如表为小李12月份第一周的苹果梨销售情况（以100kg为标准，超额记为正，不足记为负．单位：kg）．
星期
一
二
三
四
五
六
日
与标准销售量的差值
﹣3
﹣1
＋1
﹣2
﹣6
＋13
＋8
根据表格内容回答下列问题：

(1)、小李在这周星期一到星期三这三天共卖出苹果梨 kg；

(2)、这周销售量最多的一天比销售量最少的一天多销售kg；

(3)、若苹果梨的售价为5.5元/kg，小李还需要承担运费，平均运费为0.5元/kg，不考虑其他因素，求小李这周直播销售苹果梨的总收入．

查看试题解析
22. 数学中，运用整体思想方法在求整式的值时非常重要．
例如：已知m²＋3m＝1，则2m²＋6m＋1＝2（m²＋3m）＋1＝2×1＋1＝3
请你根据上面材料解答以下问题：

(1)、若n²﹣2n＝3，求2﹣n²＋2n的值；

(2)、当x＝1时，px³＋qx﹣1＝4，当x＝﹣1时，求px³＋qx﹣1的值；

(3)、当x＝2021时，ax⁵＋bx³＋cx＋2＝k，当x＝﹣2021时，直接写出ax⁵＋bx³＋cx＋2的值（用含k的式子表示）．

查看试题解析
23. （实践操作）三角尺中的数学问题．

(1)、如图1，将两块直角三角尺的直角顶点C叠放在一起，∠ACB＝∠DCH＝90°．
①若∠BCH＝36°，则∠ACD＝ ▲ ；若∠ACD＝130°，则∠BCH＝ ▲ °；
②猜想∠ACD与∠BCH之间的数量关系，并说明理由；

(2)、如图2，若是两个同样的直角三角尺，将它们60°的锐角顶点A重合在一起，∠ACB＝∠AEF＝90°，直接写出∠CAF与∠EAB之间的数量关系．

查看试题解析
24. 某乒乓球馆将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍，乒乓球拍每副定价200元，乒乓球每盒定价40元．经洽谈后，甲商店每买一副球拍赠一盒乒乓球；乙商店全部按定价的9折优惠．该球馆需买球拍5副，乒乓球若干盒（大于5盒）．

(1)、如果购买5副球拍和6盒乒乓球，则在甲商店购买需花费元，在乙商店购买需花费元；

(2)、当购买乒乓球多少盒时，在两家商店花费金额一样；

(3)、当购买乒乓球多少盒时，在乙商店购买划算．

查看试题解析
25. 某公园计划砌一个形状如图1的水池（图中长度单位：m），后有人建议改为如图2的形状，且外圆直径不变．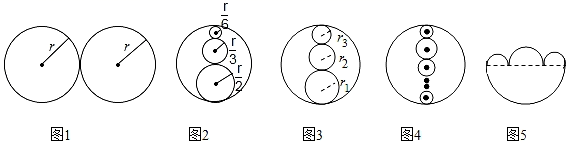

(1)、请你计算两种方案中的圆形水池的周长，确定哪一种方案砌的圆形水池的周边需要的材料多．

(2)、如图3，如果将图2中的小圆半径改为r₁ ， r₂ ， r₃ ，且r₁＋r₂＋r₃＝r，其他条件不变，猜想（1）中的结论是否改变，并说明理由．

(3)、如图4，若将图3中三个小圆改为n个小圆，小圆半径分别为r₁ ， r₂ ， …，r_n ，且r₁＋r₂＋…＋r_n＝r，直接写出图4中所有圆的周长总和．

(4)、元宝是中国古代的货币，在今天也有着富贵吉祥的寓意，王师傅准备建设一个形如元宝的花坛，如图5，花坛是由4个半圆所围成，最大半圆的半径为2.1米，直接写出花坛周边需要的材料总长（结果保留π）．

查看试题解析
26. 如图，甲、乙两人（看成点）分别在数轴﹣14和15的位置上，沿数轴做移动游戏．每次移动游戏规则：两人先进行“石头、剪刀、布”，而后根据输赢结果进行移动．
①若平局，则甲向东移动1个单位长度，同时乙向西移动1个单位长度；
②若甲赢，则甲向东移动3个单位长度，同时乙向东移动1个单位长度；
③若乙赢，则甲向西移动1个单位长度，同时乙向西移动3个单位长度．

(1)、从如图的位置开始，若完成了1次移动游戏，甲、乙“石头、剪刀、布”的结果为平局，则移动后甲、乙两人相距个单位长度；

(2)、从如图的位置开始，若完成了10次移动游戏，发现甲、乙每次都有输有赢．设乙赢了n次，且他最终停留的位置对应的数为m，试用含n的式子表示m，并求该位置距离原点O最近时n的值；

(3)、从如图的位置开始，若进行了k次移动游戏后，甲与乙的位置相距3个单位长度，直接写出k的值．

查看试题解析

星期	一	二	三	四	五	六	日
与标准销售量的差值	﹣3	﹣1	＋1	﹣2	﹣6	＋13	＋8