广东省广州市花都区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 数的倒数是( )A、 B、 C、 D、2. 2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与地球的最近距离约为55000000千米,数据55000000用科学记数法表示为( )A、55×106 B、5.5×107 C、5.5×108 D、0.55×1083. 下列方程中,解为x=2的是( )A、x+2=0 B、x﹣2=0 C、2x+1=0 D、2x﹣1=04. 下列去括号正确的是( )A、﹣(a﹣1)=﹣a+1 B、﹣(a+1)=﹣a+1 C、+(a﹣1)=+a+1 D、+(a+1)=+a﹣15. 若﹣2xay3与3x2yb是同类项,则a+b=( )A、5 B、1 C、﹣5 D、﹣16. 如图,是由4个相同的小正方体组合而成的几何体,从左面看得到的平面图形是( ).
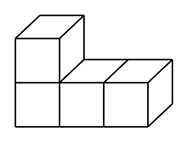 A、
A、 B、
B、 C、
C、 D、
D、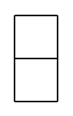 7. 下列运算错误的是( )A、 B、2ab+3ab=5ab C、 D、3ab﹣2ab=18. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
7. 下列运算错误的是( )A、 B、2ab+3ab=5ab C、 D、3ab﹣2ab=18. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、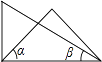 C、
C、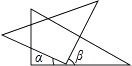 D、
D、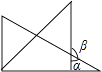 9. 某中学的学生自己动手整修操场,七年级的学生说:“如果让我们单独工作,7.5小时能完成”;八年级的学生说:“如果让我们单独工作,5小时能完成.”现两个年级学生一起工作1小时,剩下的部分再让七年级单独完成需x小时,可列方程( )A、 B、 C、 D、10. 如图(1)是一个三角形,分别连接这个三角形三边中点得到图(2),再分别连接图(2)中间的小三角形三边中点得到图(3),按这种方法继续下去,第6个图形有( )个三角形.
9. 某中学的学生自己动手整修操场,七年级的学生说:“如果让我们单独工作,7.5小时能完成”;八年级的学生说:“如果让我们单独工作,5小时能完成.”现两个年级学生一起工作1小时,剩下的部分再让七年级单独完成需x小时,可列方程( )A、 B、 C、 D、10. 如图(1)是一个三角形,分别连接这个三角形三边中点得到图(2),再分别连接图(2)中间的小三角形三边中点得到图(3),按这种方法继续下去,第6个图形有( )个三角形.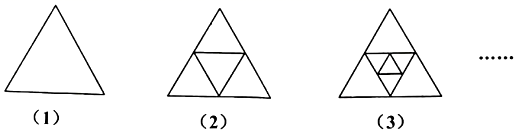 A、20 B、21 C、22 D、23
A、20 B、21 C、22 D、23二、填空题
-
11. 如果向东走35米记作+35米,那么向西走50米记作 米.12. 化简:2xy﹣xy= .13. 将12°12'化成度是 °.14. 如图,射线OA的方向是北偏西65 ,射线OB的方向是南偏东20°,则 的度数为.
 15. 如图,数轴上的点A表示有理数a,若点A到原点O的距离大于1,则|a+1|= .
15. 如图,数轴上的点A表示有理数a,若点A到原点O的距离大于1,则|a+1|= . 16. 如图所示为一个数值运算程序,当输入大于1的正整数x时,输出的结果为8,则输入的x值为 .
16. 如图所示为一个数值运算程序,当输入大于1的正整数x时,输出的结果为8,则输入的x值为 .
三、解答题
-
17. 计算(1)、(﹣11)+(﹣5)+14(2)、2×(﹣1)2021﹣20÷(﹣4)18. 解下列方程(1)、5x﹣4=2x+2(2)、19. 先化简,再求值:4(1﹣3y+x2)﹣3(x2﹣3y+2),其中x=﹣3,y=4.20. 某公司5天内货品进出仓库的吨数如下:+23,﹣30,﹣16,35,﹣33(其中“+”表示进库,“﹣”表示出库)(1)、经过这5天,仓库管理员结算后确定仓库里还有货品509吨,那么5天前仓库里存有货品多少吨?(2)、如果进出货的装卸费都是每吨4元,那么这5天一共要付多少元装卸费?21. 如图,△ABC中,∠BAC=90°,点D是BC上的一点,将△ABC沿AD翻折后,点B恰好落在线段CD上的B'处,且AB'平分∠CAD.求∠BAB'的度数.
 22. 一本课外读物共有80页,小明计划用3天时间阅读完.已知小明第一天阅读了x页,第二天阅读的页数比第一天的2倍少30页,第三天阅读的页数比第一天的多20页.求小明这三天分别阅读了多少页.23. 如图,已知线段m,n(m<n).
22. 一本课外读物共有80页,小明计划用3天时间阅读完.已知小明第一天阅读了x页,第二天阅读的页数比第一天的2倍少30页,第三天阅读的页数比第一天的多20页.求小明这三天分别阅读了多少页.23. 如图,已知线段m,n(m<n). (1)、尺规作图:在射线AE上截取AC=m,CB=n,使得AB=m+n(保留作图痕迹,不用写作法);(2)、在(1)的条件下,若点O是AB的中点,当m=3,n=5时,求线段OC的长;(3)、在(1)的条件下,若点O是AB的中点,点D是AO的中点,则线段CD=(用含mn的代数式表示).24. 七年级准备组织学生到某社会实践基地参加社会实践活动,门票价为每人20元,由各班班长负责买票.下面是1班班长与售票员咨询的对话:
(1)、尺规作图:在射线AE上截取AC=m,CB=n,使得AB=m+n(保留作图痕迹,不用写作法);(2)、在(1)的条件下,若点O是AB的中点,当m=3,n=5时,求线段OC的长;(3)、在(1)的条件下,若点O是AB的中点,点D是AO的中点,则线段CD=(用含mn的代数式表示).24. 七年级准备组织学生到某社会实践基地参加社会实践活动,门票价为每人20元,由各班班长负责买票.下面是1班班长与售票员咨询的对话: (1)、1班学生人数为44,选择了方案一购票,求1班购票需要多少元?(2)、2班选择了方案二,购票费用为702元,求2班有多少人?(3)、3班的学生人数为a(a>40),如果你是3班班长,请你从两种方案中为3班选出一种最实惠的购票方案,并说明理由.25. (阅读材料)
(1)、1班学生人数为44,选择了方案一购票,求1班购票需要多少元?(2)、2班选择了方案二,购票费用为702元,求2班有多少人?(3)、3班的学生人数为a(a>40),如果你是3班班长,请你从两种方案中为3班选出一种最实惠的购票方案,并说明理由.25. (阅读材料)我们知道,“角”是由一条射线绕着它的端点旋转而成的图形.射线在单位时间内以固定的角度绕其端点沿某一方向旋转,经过不同的旋转时间都会形成不同的角.
在行程问题中,我们知道:运动路程=运动速度×运动时间;
类似的,在旋转问题中,我们规定:旋转角度=旋转角速度×旋转时间.
例如(如图),射线OM从射线OA出发,以每秒10°的旋转速度(称为“旋转角速度”)绕点逆时针旋转.旋转1秒得旋转角度∠MOA=10°×1=10°,旋转2秒得旋转角度∠MOA=10°×2=20°,……,旋转t秒得旋转角度∠MOA=10°×t=(10t)°.
(问题解决)
如图1,射线OA上有两点M、N.将射线OM以每秒10°的旋转角速度绕点O逆时针旋转(OM最多旋转9秒);射线OM旋转3秒后,射线ON开始以每秒20°的旋转角速度绕点O逆时针旋转,如图2所示.设射线ON旋转时间为t秒.
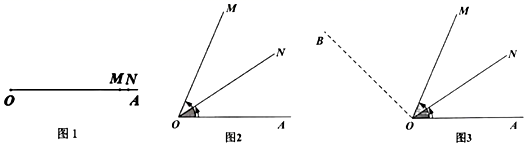 (1)、当t=2时,∠MON=°;(2)、当∠MON=20°时,求t的值;(3)、如图3,OM、ON总是在某个角∠AOB的内部旋转,且当ON为∠AOB的三等分线时,OM恰好平分∠AOB,求∠AOB的度数.
(1)、当t=2时,∠MON=°;(2)、当∠MON=20°时,求t的值;(3)、如图3,OM、ON总是在某个角∠AOB的内部旋转,且当ON为∠AOB的三等分线时,OM恰好平分∠AOB,求∠AOB的度数.