北京市顺义区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 下列各式中结果为负数的是( )A、 B、 C、 D、2. 北京2022年冬奥会计划使用25个场馆.国家速滑馆是主赛区的标志性场馆,也是唯一新建的冰上比赛场馆,冰表面积为12000平方米.数字12000用科学记数法表示为( )A、 B、 C、 D、3. 实数a , b在数轴上对应点的位置如图所示,则下列结论正确的是( )
 A、 B、 C、 D、4. 下列是一元一次方程的是( )A、 B、 C、 D、5. 方程的解是( )A、0 B、5 C、-5 D、6. 下列图形中,能用 , , 三种方法表示同一个角的是( )A、
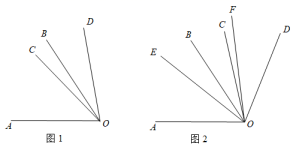
A、 B、 C、 D、4. 下列是一元一次方程的是( )A、 B、 C、 D、5. 方程的解是( )A、0 B、5 C、-5 D、6. 下列图形中,能用 , , 三种方法表示同一个角的是( )A、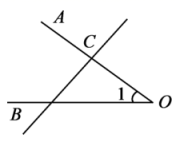 B、
B、 C、
C、 D、
D、 7. 下列变形中,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则8. 已知A、B、C、D为直线l上四个点,且 , , 点D为线段AB的中点,则线段CD的长为( )A、1 B、4 C、5 D、1或5
7. 下列变形中,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则8. 已知A、B、C、D为直线l上四个点,且 , , 点D为线段AB的中点,则线段CD的长为( )A、1 B、4 C、5 D、1或5二、填空题
-
9. .10. 在有理数-3, , 0, , -1.2,5中,整数有 , 负分数有 .11. .12. 已知 , , 则度分.13. 已知关于的方程的解为 , 写出一组满足条件的 , 的值: , .14. 小硕同学解方程的过程如下:
解:移项,得 .
合并同类项,得 .
把未知数的系数化为1,得 .
所以方程的解是 .
其中,第一步移项的依据是 .
15. 已知一个长为 , 宽为的长方形,如图1所示,沿图中虚线裁剪成四个相同的小长方形,按图2的方式拼接,则阴影部分正方形的边长是.(用含的代数式表示) 16. 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图所示,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
16. 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图所示,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?设生产圆形铁片的工人有人,则生产长方形铁片的工人有人,依题意可列方程为 .
 17. 如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的 . (填序号)
17. 如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的 . (填序号)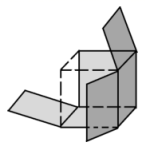
 18. 某公园划船项目收费标准如下:
18. 某公园划船项目收费标准如下:船型
两人船(限乘两人)
四人船(限乘四人)
六人船(限乘六人)
八人船(限乘八人)
每船租金(元/小时)
100
110
140
160
某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为元.
三、解答题
-
19. 计算: .20. 计算: .21. 计算: .22. 请你画一条数轴,并把2,-1,0, , 这五个数在数轴上表示出来.23. 解方程: .24. 下面是按一定规律得到的一列数:
, 第1个数是-1;
, 第2个数是;
, 第3个数是-1;
, 第4个数是;
……
按照以上规律用算式分别表示出第8和第10个数,并比较这两个数的大小.
25. 如图1所示,两个村庄A,B在河流l的两侧,现要在河边修建一个水泵站,同时向A、B两村供水,要使所铺设的管道最短,水泵站Р应该建在什么位置?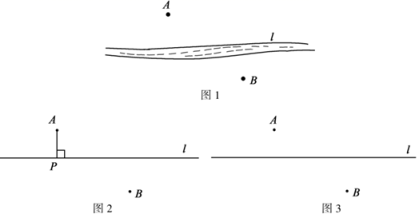
把河流近似看作直线 , 如图2所示.小明提出了这样的方案:过点A作直线的垂线段AP,则点P为水泵站的位置.你同意小明的方案吗?若同意,请说明理由.若不同意,那么你认为水泵站Р应该建在什么位置?请在图3中作出来,并说明依据.
26. 先化简,再求值:已知 ,其中 , .27. 如图,已知点C为线段AB的中点,点D为线段AB外一点,按要求完成下列问题: (1)、作直线CD,测量的度数为(精确到度);(2)、在直线CD上任取一点E,测量E,A两点之间的距离为 , E,B两点之间的距离为(精确到mm);(3)、作射线DA,DB,测量的度数为 , 的度数为(精确到度).28. 某校组织学生参加冬奥会知识竞赛,共设20道单项选择题,各题分值相同,每题必答,下表是部分参赛者的得分统计表:
(1)、作直线CD,测量的度数为(精确到度);(2)、在直线CD上任取一点E,测量E,A两点之间的距离为 , E,B两点之间的距离为(精确到mm);(3)、作射线DA,DB,测量的度数为 , 的度数为(精确到度).28. 某校组织学生参加冬奥会知识竞赛,共设20道单项选择题,各题分值相同,每题必答,下表是部分参赛者的得分统计表:参赛者
答对题数
答错题数
得分
于潇
20
0
100
王晓林
18
2
88
李毅
10
10
40
…
…
…
…
(1)、根据表格提供的数据,答对1题得分,答错1题扣分;(2)、参赛者李小萌得了76分,求她答对了几道题.