北京市密云区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的圆柱体从正面看得到的图形可能是（）

A、 B、 C、 D、

查看试题解析
2. 单项式-3mn²的系数是（）

A、9 B、-3 C、3 D、-9

查看试题解析
3. 据报道，北京2022年冬奥会标志性场馆“冰丝带”——国家速滑馆于2021年4月30日完成首次全冰面制冰，冰面面积约12000平方米，是目前亚洲最大的冰面．将12000用科学记数法表示应为（）

A、0.12×10⁵ B、1.2×10⁵ C、1.2×10⁴ D、12×10³

查看试题解析
4. 如图，数轴上点A，B表示的数互为相反数，且AB＝4，则点A表示的数是（）

A、4 B、-4 C、2 D、-2

查看试题解析
5. 修建高速公路时，经常把弯曲的公路改成直道，从而缩短路程，其道理用数学知识解释正确的是（）

A、线段可以比较大小 B、线段有两个端点 C、两点之间，线段最短 D、过两点有且只有一条直线

查看试题解析
6. 在下列式子中变形正确的是（）

A、如果 $a = b$ ，那么 $a + c = b - c$ B、如果 $a = b$ ，那么 $- 2 a = - 2 b$ C、如果 $\frac{a}{2} = 8$ ，那么 $a = 4$ D、如果 $a + b = 0$ ，那么 $a = b$

查看试题解析
7. 如图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学补画的情况（图中阴影部分），其中正确的是（）

A、 B、 C、 D、

查看试题解析
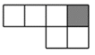8. 英国伦敦博物馆保存着一部极其珍贵的文物——纸草书，这是古代埃及人用象形文字写在一种用纸莎草压制成的草片上的著作，它于公元前1700年左右写成．这部书中，记载着这样一个数学问题：“一个数，它的全部，加上它的七分之一，其和等于19”．若设这个数是x，则可以列一元一次方程表示为（）

A、 $7 + x = 19$ B、 $7 x + x = 19$ C、 $x + \frac{1}{7} = 19$ D、 $x + \frac{1}{7} x = 19$

查看试题解析

二、填空题

9. 比较有理数的大小：-4-6．（填“>”或“<”或“=”）

查看试题解析
10. “x的3倍与y的差”用代数式可以表示为．

查看试题解析
11. ∠AOB的大小可由量角器测得（如图所示），则∠AOB的补角的大小为度．

查看试题解析
12. 写出单项式 $- \frac{1}{4} x y^{3}$ 的一个同类项为．

查看试题解析
13. 用四舍五入法将0.03057取近似数并精确到0.001，得到的值是．

查看试题解析
14. 如果关于x的方程5x-4＝2a+x的解是x＝3，那么a的值是．

查看试题解析
15. 从2020年3月开始，一群野生亚洲象从云南西双版纳傣族自治州走出丛林，一路北上，历经17个月迁徙逾500公里安全返回栖息地，引发国内外一波“观象热潮”．象群北移途经峨山县时，一头亚洲象曾脱离象群．如图，A，B，C分别表示峨山县、象群位置、独象位置．经测量，象群在峨山县的西北方向，独象在峨山县的北偏西 $16 ° 48$ 方向，则∠BAC=度分．

查看试题解析

三、解答题

16. 数学课上，老师要求同学们用一副三角板作一个钝角，并且作出它的角平分线．雯雯设计的作法如下：
⑴先按照图1的方式摆放一副三角板，画出∠AOB；

⑵在∠AOB处，再按照图2 的方式摆放一副三角板，作出射线OC；

⑶去掉三角板后得到的图形（如图3）为所求作，老师说雯雯的作法符合要求，是正确的．

请你回答：

(1)、雯雯作的∠AOB的度数是；

(2)、射线OC是∠AOB的角平分线的依据是．

查看试题解析
17. 计算： $20 - (- 6) - | - 3 |$

查看试题解析
18. 计算： $(- 8) \times (- \frac{7}{8}) - (- 36) \div (+ 9)$

查看试题解析
19. 计算： $(\frac{1}{3} - \frac{5}{6} + \frac{7}{9}) \times (- 18)$

查看试题解析
20. 计算： ${(- 1)}^{3} - \frac{1}{4} \times [2 - {(- 3)}^{2}]$ ．

查看试题解析
21. 解关于x的方程： $6 x - 3 = 15 x + 24$

查看试题解析
22. 解关于x的方程： $\frac{4 x + 1}{3} = 1 + \frac{2 x - 1}{6}$

查看试题解析
23. 先化简，再求值： $4 (x^{2} + 2) - 3 (x^{2} - x)$ ，其中 $x^{2} + 3 x - 5 = 0$ ．

查看试题解析
24. 已知：线段AB = 6，点C是线段AB的中点，延长线段AB到D，使BD= 3BC．求线段AD的长．

查看试题解析
25. 如图，已知线段a与线段b，点O在直线MN上，点A在直线MN外．

(1)、请利用直尺和圆规，按照下列要求作图（保留作图痕迹，不写作法）．
①作线段OA；
②在射线OM上作线段OB＝a，并作直线AB；
③在射线ON上取一点C，使OC＝b，并作射线AC；

(2)、写出图中的一个以A为顶点的锐角：．

查看试题解析

26. 随着民众健康意识逐步增强，全民健身逐渐成为“健康中国”新时尚．下表是甲、乙两人某月参与游泳和瑜伽项目的运动次数及时间的统计表，其中同一健身项目每人每次运动的时间相同，且甲、乙两人每次游泳的时间为2小时．

	游泳次数	瑜伽次数	两项运动的总时长（单位：小时）
甲	18	12	54
乙			41

(1)、结合表中数据，直接写出两人每次参与瑜伽运动的时间为小时；

(2)、若乙参与两项运动的总次数是24次，求乙分别参与游泳和瑜伽项目各多少次？

查看试题解析

27. 已知：∠AOB=120°，∠COD=90°，OE平分∠AOD．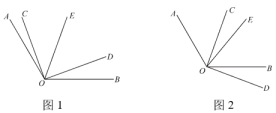

(1)、如图1，当∠COD的边OD在∠AOB内部时，若∠COE=40°，求∠BOD的度数；

(2)、如图2，当∠COD的边OD在∠AOB外部，且0°<∠BOD<60°时，设∠COE=α，∠BOD=β，用等式表示α与β之间的数量关系，并证明．

查看试题解析
28. 对于数轴上的点P，Q，我们把点P与点Q两点之间的距离记作d_[PQ] ．例如，在数轴上点P表示的数是5，点Q表示的数是2，则点P与点Q两点之间的距离为d_[PQ]=3．已知点O为数轴原点，点A表示的数为-1，点B表示的数为5．

(1)、d_[OA]= ；d_[AB]= ．

(2)、点C在数轴上表示的数为x，且点C在点A左侧，当满足d_[AC]= $\frac{1}{2}$ d_[BC]时，求x的值．

(3)、若点E表示的数为m，点F表示的数为m+2，且d_[AF]是d_[BE]的3倍，求m的值．

查看试题解析