北京市怀柔区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{3}{2}$ 的相反数是（）．

A、 $- \frac{2}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

查看试题解析
2. 第24届冬季奥林匹克运动会，将于2022年2月4日在北京开幕．此次冬奥会的单板大跳台项目场馆坐落在北京市首钢园区的北京冬季奥林匹克公园，园区总占地面积171.2公顷即1712000平方米．将1712000用科学记数法表示应为（）

A、 $1712 \times 1 0^{3}$ B、 $1.712 \times 1 0^{7}$ C、 $1.712 \times 1 0^{6}$ D、 $0.1712 \times 1 0^{7}$

查看试题解析
3. 如图是某个几何体的展开图，该几何体是（）

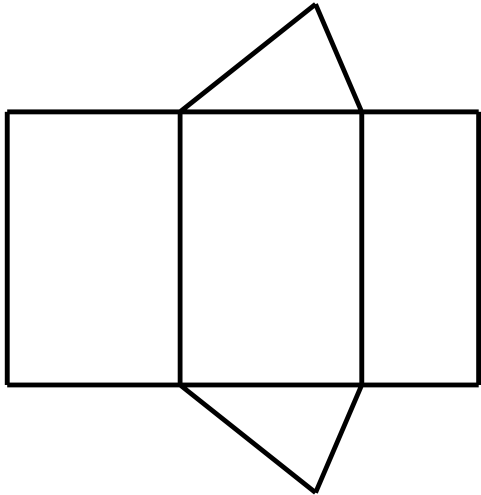A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱

查看试题解析
4. 有理数 $a ， b$ 在数轴上对应点的位置如图所示，下列结论中正确的是（）

A、 $| a | < 2$ B、 $a + b > 0$ C、 $- a > b$ D、 $b - a < 0$

查看试题解析
5. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $a - 2 a = - a$ C、 $5 a b^{2} - 2 a^{2} b = 3 a b^{2}$ D、 $2 a + 3 a = 5 a^{2}$

查看试题解析
6. 一副三角板按如图所示的方式摆放，则∠1补角的度数为（）

A、 $45 °$ B、 $135 °$ C、 $75 °$ D、 $165 °$

查看试题解析
7. 在如图所示的几何体中，从不同方向看得到的平面图形中有长方形的是（）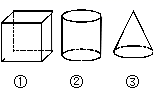

A、① B、② C、①② D、①②③

查看试题解析
8. 已知关于 $x$ 的方程 $10 - 2 x = a x$ 的解是 $x = 2$ ，则 $a$ 的值为（）

A、3 B、 $\frac{2}{3}$ C、 $\frac{5}{2}$ D、－3

查看试题解析
9. 中国古代大建筑群平面中统率全局的轴线称为“中轴线”，北京中轴线是古代中国独特城市规划理论的产物，故宫是北京中轴线的重要组成部分．故宫中也有一条中轴线，北起神武门经乾清宫、保和殿、太和殿、南到午门，这条中轴线同时也在北京城的中轴线上．图中是故宫博物院的主要建筑分布图．其中，点A表示养心殿所在位置，点O表示太和殿所在位置，点B表示文渊阁所在位置．已知养心殿位于太和殿北偏西 $21 ° 18$ 方向上，文渊阁位于太和殿南偏东 $58 ° 18$ 方向上，则∠AOB的度数是（）

A、 $79 ° 36$ B、 $143 °$ C、 $140 °$ D、 $153 °$

查看试题解析
10. 如图是某月的月历，用一个方框任意框出4个数a，b，c，d．若2a＋d－b＋c的值为68，那么a的值为（）

A、13 B、18 C、20 D、22

查看试题解析

二、填空题

11. 写出一个比 $- 3$ 大的负有理数．

查看试题解析
12. 用四舍五入法取近似数： $3.2652 \approx$ （精确到百分位）．

查看试题解析
13. 请写出一个只含有字母a，b，且系数为－1，次数为5的单项式．

查看试题解析
14. 怀柔北部山区的分水岭隧道全长3333米，是我区最长的隧道．建成后有效缩短了我区北部乡镇居民往返怀柔城区的路程．如图，你能用学过的数学知识来解释走分水岭隧道与原盘山路相比缩短路程的原因吗？．

查看试题解析
15. 若单项式 $- 2 a^{2 m} b^{3}$ 与 $3 a^{2} b^{n - 1}$ 为同类项，则m－n＝．

查看试题解析
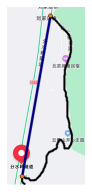16. 小明的妈妈2021年在某商场消费一年共得532积分，该商场每年一月份进行积分换购活动，全商场都参与此活动．规则：一积分可充当一元钱进行消费，消费款优先从积分扣除，若积分不足则不足部分以现金结算．今年1月份，小明的妈妈在此商场超市消费238元，又准备在女鞋部购买一双售价330元的皮鞋，请回答她应如何支付：．

查看试题解析
17. 若AB＝6cm，点C是直线AB上一点，BC＝2cm，D是线段AC的中点，则线段AD的长度为cm．

查看试题解析
18. 已知，数轴上A，B，C三点对应的有理数分别为a，b，c．其中点A在点B左侧，A，B两点间的距离为2，且a，b，c满足 $| a + b | + (c - 2022)^{2} = 0$ ，则a＝．对数轴上任意一点P，点P对应数x，若存在x使 $| x - a | + | x - b | + | x - c |$ 的值最小，则x的值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $| - 2 | - (- 1) + (- 3)$ ；

(2)、 $(- 2)^{2} - [(- 1)^{3} + (1 - 5) \div (- 1 \frac{1}{3})]$ ．

查看试题解析
20. 已知 $4 a^{2} - 5 a + 1 = 0$ ，求代数式 $（ 3 a^{2} - 2 a) - \frac{1}{2} (2 a^{2} + a - 1)$ 的值．

查看试题解析
21.

(1)、用方程解答： $x$ 的5倍与2的和等于 $x$ 的3倍与4的差，求 $x$ ．
将下列解答过程补充完整：

列方程为：                  ▲                  ；

解方程，移项：                  ▲                  （依据                  ▲                  ）；

移项的目的：                  ▲                  ；

解得：                  ▲

(2)、小刚解方程 $3 x + \frac{x - 1}{2} = 3 - \frac{1}{3} (2 x - 1)$ 去分母时出现了错误，请你能帮他改正，解答下列问题．
解：去分母，得 $6 x + 3 x - 1 = 9 - 2 (2 x - 1)$ ；

改为：                  ▲                   ，（依据                  ▲                  ）；

去括号，得                  ▲                   ，（依据                  ▲                  ）；

解得：                  ▲

查看试题解析
22. 如图，平面内有两个点A，B．应用量角器、圆规和带刻度的直尺完成下列画图或测量：
（1 ）经过A，B两点画直线，写出你发现的基本事实；
（2 ）利用量角器在直线AB一侧画 $∠ A B C = 40 °$ ；
（ 3 ）在射线BC上用圆规截取BD＝AB（保留作图痕迹）；
（ 4 ）连接AD，取AD中点E，连接BE；
（ 5 ）通过作图我们知道． $A B = B D ， A E = D E$ ，观察并测量图形中的角，写出一组你发现的两个角之间可能存在的数量关系．

查看试题解析
23. 为响应国家节能减排政策，某班开展了节电竞赛活动．通过随手关灯、提高夏季空调温度、及时关闭电源等行为小明和小玲两位同学半年共节电55度．据统计，节约1度电相当于减排0.997千克“二氧化碳”，在节电55度产生的减排量中，若小明减排量的2倍比小玲多19.94千克．设小明半年节电x度．请回答下面的问题：

(1)、用含x的代数式表示小玲半年节电量为度，用含x的代数式表示这半年小明节电产生的减排量为千克，用含x的代数式表示这半年小玲节电产生的减排量为千克．

(2)、请列方程求出小明半年节电的度数．

查看试题解析
24. 完成下列说理过程（括号中填写推理的依据）：
已知：如图，直线AB，CD相交于点O， $O E 平分 ∠ A O F ， ∠ C O E = 90 °$ ．求证： $∠ F O B = 2 ∠ A O C$ ．
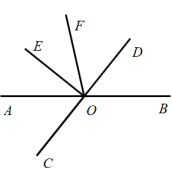
证明： $∵ O E 平分 ∠ A O F$ ，
$∴ ∠ A O E = ∠ E O F$ ．（                  ▲                  ）
$∵ ∠ C O E = 90 °$ ，
$∴ ∠ A O C + ∠ A O E = 90 °$ ．
$∵$ 直线AB，CD相交于点O，
$∴ ∠ E O D = 180 ° - ∠ C O E = 90 °$ ．
$∴$ $∠ E O F + ∠ F O D = 9 0^{∘}$ ．
$∴$ $∠ A O C$ ＝                  ▲                   ．（                  ▲                  ）
$∵$ 直线 $A B ， C D$ 相交于 $O$ ，
$∴ ∠ A O C + ∠ A O D = 180 ° ， ∠ A O D + ∠ B O D = 180 °$ ．
$∴$                   ▲                   ．（                  ▲                  ）
$∴ ∠ F O B = ∠ F O D + ∠ B O D = 2 ∠ A O C$ ．

查看试题解析
25. 有理数a，b如果满足 $a + b = a \cdot b$ ，那么我们定义a，b为一组团结数对，记为＜a，b＞．例如： $- 1$ 和 $\frac{1}{2}$ ，因为 $- 1 + \frac{1}{2} = - \frac{1}{2} ， - 1 \times \frac{1}{2} = - \frac{1}{2}$ ，所以 $- 1 + \frac{1}{2} = - 1 \times \frac{1}{2}$ ，则称 $- 1$ 和 $\frac{1}{2}$ 为一组团结数对，记为＜ $- 1 ， \frac{1}{2}$ ＞．
根据以上定义完成下列各题：

(1)、找出2和2，1和3，－2和 $\frac{2}{3}$ 这三组数中的团结数对，记为；

(2)、若＜5，x＞成立，则x的值为；

(3)、若＜a，b＞成立，b为按一定规律排列成1，－3，9，－27，81，－243，……这列数中的一个，且b与b左右两个相邻数的和是567，求a的值．

查看试题解析
26. 已知，点 $A$ ， $B$ 是数轴上不重合的两个点，且点 $A$ 在点 $B$ 的左边，点 $M$ 是线段 $A B$ 的中点．点A，B，M分别表示数a，b，x．请回答下列问题．

(1)、若a＝－1，b＝3，则点A，B之间的距离为；

(2)、如图，点A，B之间的距离用含 $a$ ， $b$ 的代数式表示为x＝，利用数轴思考x的值，x＝（用含 $a$ ， $b$ 的代数式表示，结果需合并同类项）；

(3)、点C，D分别表示数c，d．点C，D的中点也为点M，找到 $a ， b ， c ， d$ 之间的数量关系，并用这种关系解决问题（提示：思考x的不同表示方法，找相等关系）．
①若a＝－2，b＝6，c＝ $\frac{7}{3}$ 则d＝；
②若存在有理数t，满足b＝2t＋1，d＝3t－1，且a＝3，c＝－2，则t＝；
③若A，B，C，D四点表示的数分别为－8，10，－1，3．点A以每秒4个单位长度的速度向右运动，点B以每秒3个单位长度的速度向左运动，点C以每秒2个单位长度的速度向右运动，点D以每秒3个单位长度的速度向左运动，若t秒后以这四个点为端点的两条线段中点相同，则t＝．

查看试题解析