北京市丰台区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. ﹣3的相反数为( )A、﹣3 B、﹣ C、 D、32. 经过全党全国各族人民共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,将9899用科学记数法表示应为( )A、 B、 C、 D、3. 如图是一个几何体的表面展开图,这个几何体是( )
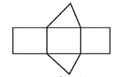 A、
A、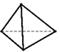 B、
B、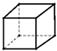 C、
C、 D、
D、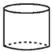 4. 下列四个数中,是负数的是( )A、|﹣4| B、﹣(﹣4) C、(﹣4)2 D、﹣425. 如图,O是直线AB上一点,则图中互为补角的角共有( )
4. 下列四个数中,是负数的是( )A、|﹣4| B、﹣(﹣4) C、(﹣4)2 D、﹣425. 如图,O是直线AB上一点,则图中互为补角的角共有( )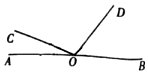 A、1对 B、2对 C、3对 D、4对6. 如图是我国某市12月份连续4天的天气预报数据,其中日温差最大的一天是( )
A、1对 B、2对 C、3对 D、4对6. 如图是我国某市12月份连续4天的天气预报数据,其中日温差最大的一天是( ) A、12月13日 B、12月14日 C、12月15日 D、12月16日7. 下面计算正确的( )A、 B、 C、 D、8. 只借助一副三角尺拼摆,不能画出下列哪个度数的角( )A、15° B、65° C、75° D、135°9. 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
A、12月13日 B、12月14日 C、12月15日 D、12月16日7. 下面计算正确的( )A、 B、 C、 D、8. 只借助一副三角尺拼摆,不能画出下列哪个度数的角( )A、15° B、65° C、75° D、135°9. 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( ) A、|a|>|b| B、a+b<0 C、a﹣b<0 D、ab>010. 如图是用棋子摆成的图案,按照这样的规律摆下去,第9个图案需要的棋子个数为( )
A、|a|>|b| B、a+b<0 C、a﹣b<0 D、ab>010. 如图是用棋子摆成的图案,按照这样的规律摆下去,第9个图案需要的棋子个数为( ) A、81 B、91 C、109 D、111
A、81 B、91 C、109 D、111二、填空题
-
11. 单项式5x2y的系数是 , 次数是 .12. 任意写出一个绝对值大于1的负有理数.13. 在日常生活和生产中有很多现象可以用数学知识进行解释.如图,要把一根挂衣帽的挂钩架水平固定在墙上,至少需要钉个钉子.用你所学数学知识说明其中的道理 .
 14. 关于x的一元一次方程2x+m=6的解为x=2,则m的值为 .15. 如图,阴影部分的面积是 .
14. 关于x的一元一次方程2x+m=6的解为x=2,则m的值为 .15. 如图,阴影部分的面积是 . 16. 《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作.其中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是:有若干人共同购买某种物品,如果每人出8钱,则多3钱;如果每人出7钱,则少4钱,问共有多少人?物品的价格是多少钱?用一元一次方程的知识解答上述问题设共有x人,依题意,可列方程为 .
16. 《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作.其中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是:有若干人共同购买某种物品,如果每人出8钱,则多3钱;如果每人出7钱,则少4钱,问共有多少人?物品的价格是多少钱?用一元一次方程的知识解答上述问题设共有x人,依题意,可列方程为 .
 17. 如图,延长线段AB到C,使BC=AB,D为线段AC的中点,若DC=3,则AB= .
17. 如图,延长线段AB到C,使BC=AB,D为线段AC的中点,若DC=3,则AB= . 18. 历史上数学家欧拉最先把关于x的多项式用记号f(x)表示,把x等于某数a时的多项式的值用f(a)表示.例如多项式f(x)=x2﹣x+1,当x=4时,多项式的值为f(4)=42﹣4+1=13,已知多项式f(x)=mx3+nx+3,若f(1)=12,则f(﹣1)的值为 .
18. 历史上数学家欧拉最先把关于x的多项式用记号f(x)表示,把x等于某数a时的多项式的值用f(a)表示.例如多项式f(x)=x2﹣x+1,当x=4时,多项式的值为f(4)=42﹣4+1=13,已知多项式f(x)=mx3+nx+3,若f(1)=12,则f(﹣1)的值为 .三、解答题
-
19. 计算:(﹣12)﹣5+(﹣14)﹣(﹣39).20. 计算:(﹣45)÷(﹣9)+4×(﹣)21. 计算:﹣24+|6﹣10|﹣3×(﹣1)522. 解方程:=2 .23. 如图,点A,B,C是同一平面内三个点,按要求画图,并回答问题.
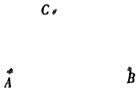 (1)、画直线AB;(2)、画射线AC,用圆规在线段AC的延长线上截取CD=AC(保留作图痕迹);(3)、连接BD,观察图形发现,AD+BD>AB,得出这个结论的依据是 .24. 先化简,再求值:b2﹣a2+2(a2+ab)﹣(a2+b2),其中a= , b= .25. 补全解题过程.
(1)、画直线AB;(2)、画射线AC,用圆规在线段AC的延长线上截取CD=AC(保留作图痕迹);(3)、连接BD,观察图形发现,AD+BD>AB,得出这个结论的依据是 .24. 先化简,再求值:b2﹣a2+2(a2+ab)﹣(a2+b2),其中a= , b= .25. 补全解题过程.已知:如图,∠AOB=40°,∠BOC=70°,OD平分∠AOC.
求∠BOD的度数.
解:∵∠AOB=40°,∠BOC=70°,
∴∠AOC=∠AOB+∠BOC= ▲ °.
∵OD平分∠AOC,
∴∠AOD=∠ ▲ ( ▲ )(填写推理依据).
∴∠AOD= ▲ °.
∴∠BOD=∠AOD﹣∠ ▲ .
∴∠BOD= ▲ °.
 26. 列方程解应用题:京张高铁是2022年北京冬奥会的重要交通基础设施.考虑到不同路段的特殊情况,将根据不同的运行区间设置不同的时速.其中,北京北站到清河段全长11千米,分为地下清华园隧道和地上区间两部分,地下清华园隧道运行速度为80千米/小时.地上区间运行速度为120千米/小时.按此运行速度,地下清华园隧道运行时间比地上区间运行时间多2分钟,求地下清华园隧道全长为多少千米.27. “格子乘法”作为两个数相乘的一种计算方法,最早在15世纪由意大利数学家帕乔利提出,在明代数学家程大位著的《算法统宗》一书中被称为“铺地锦”.
26. 列方程解应用题:京张高铁是2022年北京冬奥会的重要交通基础设施.考虑到不同路段的特殊情况,将根据不同的运行区间设置不同的时速.其中,北京北站到清河段全长11千米,分为地下清华园隧道和地上区间两部分,地下清华园隧道运行速度为80千米/小时.地上区间运行速度为120千米/小时.按此运行速度,地下清华园隧道运行时间比地上区间运行时间多2分钟,求地下清华园隧道全长为多少千米.27. “格子乘法”作为两个数相乘的一种计算方法,最早在15世纪由意大利数学家帕乔利提出,在明代数学家程大位著的《算法统宗》一书中被称为“铺地锦”.例如:如图1,计算46×71,将乘数46写在方格上边乘数71写在方格右边,然后用乘数46的每位数字乘以乘数71的每位数字,将结果记入相应的方格中,最后沿斜线方向相加得3266


 (1)、如图2用“格子乘法”计算两个两位数相乘,则x= , y=;(2)、如图3,用“格子乘法”计算两个两位数相乘,得2176,则m= , n=;(3)、如图4,用“格子乘法”计算两个两位数相乘,则k= .28. 已知点P,点A,点B是数轴上的三个点.若点P到原点的距离等于点A,点B到原点距离的和的一半,则称点P为点A和点B的“关联点”.(1)、已知点A表示1,点B表示﹣3,下列各数﹣2,﹣1,0,2在数轴上所对应的点分别是P1 , P2 , P3 , P4 , 其中是点A和点B的“关联点”的是;(2)、已知点A表示3,点B表示m,点P为点A和点B的“关联点”,且点P到原点的距离为5,求m的值;(3)、已知点A表示a(a>0),将点A沿数轴正方向移动4个单位长度,得到点B.当点P为点A和点B的“关联点”时,直接写出PB﹣PA的值.
(1)、如图2用“格子乘法”计算两个两位数相乘,则x= , y=;(2)、如图3,用“格子乘法”计算两个两位数相乘,得2176,则m= , n=;(3)、如图4,用“格子乘法”计算两个两位数相乘,则k= .28. 已知点P,点A,点B是数轴上的三个点.若点P到原点的距离等于点A,点B到原点距离的和的一半,则称点P为点A和点B的“关联点”.(1)、已知点A表示1,点B表示﹣3,下列各数﹣2,﹣1,0,2在数轴上所对应的点分别是P1 , P2 , P3 , P4 , 其中是点A和点B的“关联点”的是;(2)、已知点A表示3,点B表示m,点P为点A和点B的“关联点”,且点P到原点的距离为5,求m的值;(3)、已知点A表示a(a>0),将点A沿数轴正方向移动4个单位长度,得到点B.当点P为点A和点B的“关联点”时,直接写出PB﹣PA的值.