天津市河东区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 方程x2=x的解是( )A、x=1 B、x=0 C、x1=1,x2=0 D、x1=﹣1,x2=02. 方程(x+1)(x+2)=0化为一般形式后,常数项为( )A、6 B、﹣8 C、2 D、﹣43. 点P(3,﹣2)关于原点O的对称点的坐标是( )A、(3,﹣2) B、(﹣3,2) C、(﹣3,﹣2) D、(2,3)4. 下列图形中,是中心对称图形也是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 对于二次函数 的图象,下列说法正确的是( )A、开口向上 B、对称轴是x=-3 C、当x>-4 时,y随x的增大而减小 D、顶点坐标为(-2,-3)6. 把抛物线向左平移2个单位,再向上平移3个单位,得到的抛物线是( )A、 B、 C、 D、7. 如图,AB为⊙O的直径,C、D为⊙O上两点,∠CDB=30°,BC=4.5,则AB的长度为( )
5. 对于二次函数 的图象,下列说法正确的是( )A、开口向上 B、对称轴是x=-3 C、当x>-4 时,y随x的增大而减小 D、顶点坐标为(-2,-3)6. 把抛物线向左平移2个单位,再向上平移3个单位,得到的抛物线是( )A、 B、 C、 D、7. 如图,AB为⊙O的直径,C、D为⊙O上两点,∠CDB=30°,BC=4.5,则AB的长度为( ) A、6 B、3 C、9 D、128. 下列说法正确的是( )A、掷一枚质地均匀的骰子,掷得的点数为3的概率是 B、某种彩票中奖的概率是 ,那么买10000张这种彩票一定会中奖 C、掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上,一枚硬币反面朝上”的概率相同 D、通过大量重复试验,可以用频率估计概率9. 如图, 的三个顶点都在方格纸的格点上,其中 点的坐标是 ,现将 绕 点按逆时针方向旋转 ,则旋转后点 的坐标是( )
A、6 B、3 C、9 D、128. 下列说法正确的是( )A、掷一枚质地均匀的骰子,掷得的点数为3的概率是 B、某种彩票中奖的概率是 ,那么买10000张这种彩票一定会中奖 C、掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上,一枚硬币反面朝上”的概率相同 D、通过大量重复试验,可以用频率估计概率9. 如图, 的三个顶点都在方格纸的格点上,其中 点的坐标是 ,现将 绕 点按逆时针方向旋转 ,则旋转后点 的坐标是( ) A、 B、 C、 D、10. 若点A(﹣3,y1),B(2,y2),C(5,y3)都在反比例函数y=(a为常数)的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y2<y111. 反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )A、
A、 B、 C、 D、10. 若点A(﹣3,y1),B(2,y2),C(5,y3)都在反比例函数y=(a为常数)的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y2<y111. 反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )A、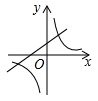 B、
B、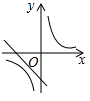 C、
C、 D、
D、 12. 抛物线的图象过点 , 对称轴为直线 , 有下列四个结论:①;②;③的最大值为3;④方程有实数根.其中正确的为( )A、①② B、①③ C、②③ D、②④
12. 抛物线的图象过点 , 对称轴为直线 , 有下列四个结论:①;②;③的最大值为3;④方程有实数根.其中正确的为( )A、①② B、①③ C、②③ D、②④二、填空题
-
13. 若m是方程2x2﹣3x﹣2=0的一个根,则﹣6m2+9m﹣13的值为 .14. 一个袋中有形状材料均相同的白球2个、红球3个,任意摸一个球是红球的概率 .15. 如图,半径为2的与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD的长为 .
 16. 抛物线y=﹣x2+2x﹣1的图象与x轴交点的个数是 .17. 有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程ax2﹣2(a﹣1)x+(a﹣3)=0有两个不相等的实数根,且使反比例函数y=的图象分布在一、三象限的概率是 .18. 如图,点C是半圆上一动点,以BC为边作正方形BCDE(使在正方形内),连OE,若AB=4cm,则OE的最大值为cm.
16. 抛物线y=﹣x2+2x﹣1的图象与x轴交点的个数是 .17. 有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程ax2﹣2(a﹣1)x+(a﹣3)=0有两个不相等的实数根,且使反比例函数y=的图象分布在一、三象限的概率是 .18. 如图,点C是半圆上一动点,以BC为边作正方形BCDE(使在正方形内),连OE,若AB=4cm,则OE的最大值为cm.
三、解答题
-
19. 解方程:(1)、x2﹣3x=0;(2)、2x(3x﹣2)=2﹣3x.20. 随着信息技术的迅猛发展,移动支付已成为一种常见的支付方式.在一次购物中,马老师和赵老师随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付.(1)、请用列表法或画树状图法,求两位老师所有可能出现的支付方式;(2)、求两位老师恰好都选择“微信”支付的概率.21. 如图,BE是的直径,点A和点D是上的两点,过点A作的切线交BE延长线于点C.
 (1)、若 , 求的度数;(2)、若 , , 求AC的长.22. 已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).(1)、试确定此二次函数的解析式;(2)、请你判断点P(-2,3)是否在这个二次函数的图象上?23. 某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系,(其中 , 且x为整数)
(1)、若 , 求的度数;(2)、若 , , 求AC的长.22. 已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).(1)、试确定此二次函数的解析式;(2)、请你判断点P(-2,3)是否在这个二次函数的图象上?23. 某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系,(其中 , 且x为整数) (1)、直接写出y与x的函数关系式;(2)、当售价为多少时,商家所获利润最大,最大利润是多少?24. 将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,其中点E与点B,点G与点D分别是对应点,连接BG.
(1)、直接写出y与x的函数关系式;(2)、当售价为多少时,商家所获利润最大,最大利润是多少?24. 将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,其中点E与点B,点G与点D分别是对应点,连接BG.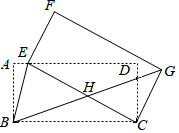 (1)、如图,若点A,E,D第一次在同一直线上,BG与CE交于点H,连接BE.
(1)、如图,若点A,E,D第一次在同一直线上,BG与CE交于点H,连接BE.①求证:BE平分∠AEC.
②取BC的中点P,连接PH,求证:PHCG.
③若BC=2AB=2,求BG的长.
(2)、若点A,E,D第二次在同一直线上,BC=2AB=4,直接写出点D到BG的距离.25. 如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,与y轴交于点A,与x轴交于点E、B.且点A(0,5),B(5,0),点P为抛物线上的一动点.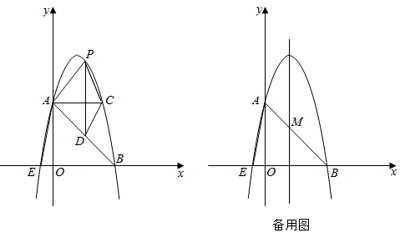 (1)、求二次函数的解析式;(2)、如图,过点A作AC平行于x轴,交抛物线于点C,若点P在AC的上方,作PD平行于y轴交AB于点D,连接PA,PC,当S四边形APCD=时,求点P坐标;(3)、设抛物线的对称轴与AB交于点M,点Q在直线AB上,当以点M、E、P、Q为顶点的四边形为平行四边形时,请直接写出点Q的坐标.
(1)、求二次函数的解析式;(2)、如图,过点A作AC平行于x轴,交抛物线于点C,若点P在AC的上方,作PD平行于y轴交AB于点D,连接PA,PC,当S四边形APCD=时,求点P坐标;(3)、设抛物线的对称轴与AB交于点M,点Q在直线AB上,当以点M、E、P、Q为顶点的四边形为平行四边形时,请直接写出点Q的坐标.