上海市杨浦区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 将函数 的图像向下平移2个单位,下列结论中,正确的是( )A、开口方向不变 B、顶点不变 C、与 轴的交点不变 D、与 轴的交点不变2. 在 Rt 中, , 如果 , 那么等于( )A、 B、 C、 D、3. 已知 和 都是单位向量, 下列结论中,正确的是( )A、 B、 C、 D、4. 已知点 是线段 上的一点,线段是和的比例中项,下列结论中,正确的是( )A、 B、 C、 D、5. 如图, 在梯形 中,ADBC,过对角线交点 的直线与两底分别交于点 , 下列结论中,错误的是( )
 A、 B、 C、 D、6. 如图,点 是 的角平分线 的中点, 点 分别在 边上,线段 过点 , 且 , 下列结论中, 错误的是( )
A、 B、 C、 D、6. 如图,点 是 的角平分线 的中点, 点 分别在 边上,线段 过点 , 且 , 下列结论中, 错误的是( )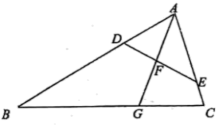 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 已知 , 那么 .8. .9. 已知抛物线 , 它与 轴的交点坐标为 .10. 二次函数 图像上的最低点的纵坐标为 .11. 已知 的长度为 的长度为 4 , 且和方向相反,用向量表示向量 .12. 如果两个相似三角形对应边之比是 , 那么它们的周长之比等于 .13. 已知在 中, , 那么 .14. 已知在 中, , 点 是 的重心, 那么点 到斜边 的距离是 .15. 在某一时刻, 直立地面的一根竹竿的影长为 3 米,一根旗杆的影长为 25 米, 已知这根竹竿的长度为 米, 那么这根旗杆的高度为米.16. 如图,海中有一个小岛A,一艘轮船由西向东航行,在点处测得小岛A在它的北偏东方向上,航行12海里到达点处,测得小岛A在它的北偏东方向上,那么小岛A到航线的距离等于海里.
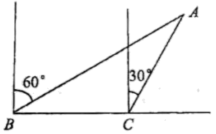 17. 新定义:已知三条平行直线, 相邻两条平行线间的距离相等, 我们把三个顺点分别在这样的三条平行 线上的三角形称为格线三角形. 如图, 已知等腰 Rt 为 “格线三角形”, 且 , 那么直线 与直线 的夹角 的余切值为 .
17. 新定义:已知三条平行直线, 相邻两条平行线间的距离相等, 我们把三个顺点分别在这样的三条平行 线上的三角形称为格线三角形. 如图, 已知等腰 Rt 为 “格线三角形”, 且 , 那么直线 与直线 的夹角 的余切值为 .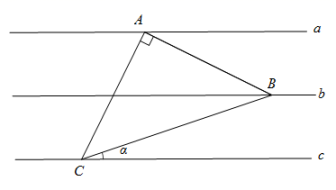 18. 如图, 已知在 Rt 中, , 将 绕点 逆时针旋转 后得 , 点 落在点 处, 点 落在点 处, 联结 , 作 的平分线 , 交线段 于点 , 交线 段 于点 , 那么 的值为 .
18. 如图, 已知在 Rt 中, , 将 绕点 逆时针旋转 后得 , 点 落在点 处, 点 落在点 处, 联结 , 作 的平分线 , 交线段 于点 , 交线 段 于点 , 那么 的值为 .
三、解答题
-
19. 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE= BC.
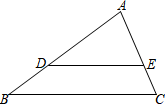 (1)、如果AC=6,求AE的长;(2)、设 , ,求向量 (用向量 、 表示).20. 已知二次函数 .(1)、用配方法把二次函数化为的形式,并指出这个函数图象的开口方向、对称轴和顶点坐标;(2)、如果将该函数图象沿轴向下平移5个单位,所得新抛物线与轴正半轴交于点 , 与轴交于点 , 顶点为 , 求的面积.21. 如图,已知在中, , 垂足为点 , 点是边的中点.
(1)、如果AC=6,求AE的长;(2)、设 , ,求向量 (用向量 、 表示).20. 已知二次函数 .(1)、用配方法把二次函数化为的形式,并指出这个函数图象的开口方向、对称轴和顶点坐标;(2)、如果将该函数图象沿轴向下平移5个单位,所得新抛物线与轴正半轴交于点 , 与轴交于点 , 顶点为 , 求的面积.21. 如图,已知在中, , 垂足为点 , 点是边的中点. (1)、求边的长;(2)、求的正弦值.22. 如图,为了测量建筑物的高度,先从与建筑物的底部点水平相距100米的点处出发,沿斜坡行走至坡顶处,斜坡的坡度 , 坡顶到的距离米,在点处测得建筑物顶端点的仰角为 , 点在同一平面内,根据测量数据,请计算建筑物的高度(结果精确到1米).(参考数据:)
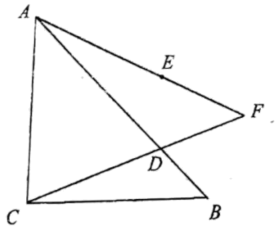
(1)、求边的长;(2)、求的正弦值.22. 如图,为了测量建筑物的高度,先从与建筑物的底部点水平相距100米的点处出发,沿斜坡行走至坡顶处,斜坡的坡度 , 坡顶到的距离米,在点处测得建筑物顶端点的仰角为 , 点在同一平面内,根据测量数据,请计算建筑物的高度(结果精确到1米).(参考数据:)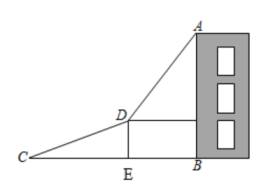 23. 已知,如图,在四边形中, , 点在边上AECD,DEAB,过点作CFAD,交线段于点 , 联结 .
23. 已知,如图,在四边形中, , 点在边上AECD,DEAB,过点作CFAD,交线段于点 , 联结 .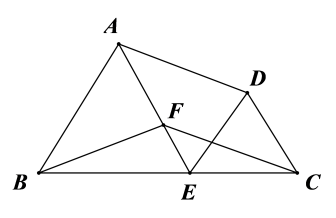 (1)、求证:;(2)、如果射线经过点 , 求证: .
(1)、求证:;(2)、如果射线经过点 , 求证: .