上海市嘉定区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 下列函数中是二次函数的是( )A、 B、 C、 D、2. 已知抛物线的顶点是此抛物线的最低点,那么的取值范围是( )A、 B、 C、 D、3. 在中, , , , 那么下列各式中正确的是( )A、 B、 C、 D、4. 在中, , , 那么的长是( )A、 B、 C、 D、5. 已知一个单位向量 , 设、是非零向量,那么下列等式中一定正确的是( )A、 B、 C、 D、6. 如图,已知 , , 那么下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 抛物线经过点 , 那么a= .8. 抛物线的对称轴是 .9. 抛物线在对称轴右侧的部分是上升的,那么的取值范围是 .10. 将抛物线向左平移2个单位,得到一条新抛物线,这条新抛物线的表达式是 .11. 在中, , , , 那么 .12. 在菱形中,对角线与之比是 , 那么 .13. 如图,飞机在目标的正上方处,飞行员测得地面目标的俯角 , 如果地面目标、之间的距离为千米,那么飞机离地面的高度等于千米.(结果保留根号)
 14. 已知 , 那么 .15. 已知向量、、满足 , 试用向量、表示向量 , 那么= .16. 如图,在中, , , , , 那么的值是 .
14. 已知 , 那么 .15. 已知向量、、满足 , 试用向量、表示向量 , 那么= .16. 如图,在中, , , , , 那么的值是 .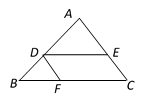 17. 在梯形中, , 对角线与相交于点 , 如果、 的面积分别是1cm2、4cm2 , 那么梯形的面积等于cm2 .18. 如图,在中, , , , 点在边上, , 联结 , 点在线段上,如果 , 那么 .
17. 在梯形中, , 对角线与相交于点 , 如果、 的面积分别是1cm2、4cm2 , 那么梯形的面积等于cm2 .18. 如图,在中, , , , 点在边上, , 联结 , 点在线段上,如果 , 那么 .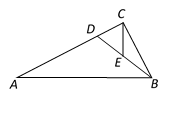
三、解答题
-
19. 计算: .20. 如图,在梯形中, , 点在线段上,与相交于点 , 与的延长线相交于点 , 已知 , , . 求、的长.
 21. 已知二次函数的图像经过点、、 .(1)、求这个二次函数的解析式;(2)、用配方法求出这个二次函数图象的顶点坐标.22. 如图,在航线的两侧分别有两个灯塔和 , 灯塔到航线的距离为千米,灯塔到航线的距离为千米,灯塔位于灯塔南偏东方向.现有一艘轮船从位于灯塔北偏西方向的(在航线上)处,正沿该航线自东向西航行,分钟后该轮船行至灯塔正南方向的点(在航线上)处.
21. 已知二次函数的图像经过点、、 .(1)、求这个二次函数的解析式;(2)、用配方法求出这个二次函数图象的顶点坐标.22. 如图,在航线的两侧分别有两个灯塔和 , 灯塔到航线的距离为千米,灯塔到航线的距离为千米,灯塔位于灯塔南偏东方向.现有一艘轮船从位于灯塔北偏西方向的(在航线上)处,正沿该航线自东向西航行,分钟后该轮船行至灯塔正南方向的点(在航线上)处.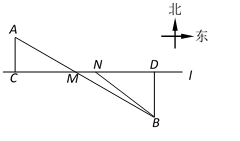 (1)、求两个灯塔和之间的距离;(2)、求该轮船航行的速度(结果精确到0.1千米/小时).(参考数据: , , , )23. 如图,已知正方形和正方形 , 点在边上,点在边的延长线上,连接 , 并延长交于点 .
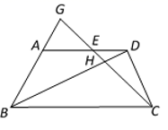
(1)、求两个灯塔和之间的距离;(2)、求该轮船航行的速度(结果精确到0.1千米/小时).(参考数据: , , , )23. 如图,已知正方形和正方形 , 点在边上,点在边的延长线上,连接 , 并延长交于点 .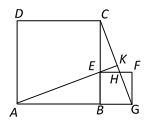 (1)、求证:∽;(2)、如果与交于点 , 求证: .24. 在平面直角坐标系中,点、两点在直线上,如图.二次函数的图像也经过点、两点,并与轴相交于点 , 如果轴,点的横坐标是 .
(1)、求证:∽;(2)、如果与交于点 , 求证: .24. 在平面直角坐标系中,点、两点在直线上,如图.二次函数的图像也经过点、两点,并与轴相交于点 , 如果轴,点的横坐标是 . (1)、求这个二次函数的解析式;(2)、设这个二次函数图象的对称轴与交于点 , 点在轴的负半轴上,如果以点、、所组成的三角形与相似,且相似比不为 , 求点的坐标;(3)、设这个二次函数图象的顶点是 , 求的值.25. 在平行四边形中,对角线与边垂直, , 四边形的周长是 , 点是在延长线上的一点,点是在射线上的一点, .
(1)、求这个二次函数的解析式;(2)、设这个二次函数图象的对称轴与交于点 , 点在轴的负半轴上,如果以点、、所组成的三角形与相似,且相似比不为 , 求点的坐标;(3)、设这个二次函数图象的顶点是 , 求的值.25. 在平行四边形中,对角线与边垂直, , 四边形的周长是 , 点是在延长线上的一点,点是在射线上的一点, .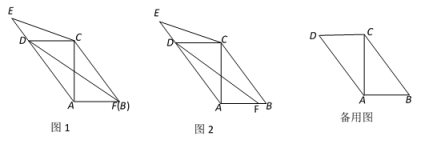 (1)、如图1,如果点与点重合,求的余切值;(2)、如图2,点在边上的一点.设 , , 求关于的函数关系式并写出它的定义域;(3)、如果 , 求的面积.
(1)、如图1,如果点与点重合,求的余切值;(2)、如图2,点在边上的一点.设 , , 求关于的函数关系式并写出它的定义域;(3)、如果 , 求的面积.