山西省运城市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $x (x - 2) = x$ 的根为（）

A、 $x = 0$ B、 $x_{1} = 2$ ， $x_{2} = 0$ C、 $x = 3$ D、 $x_{1} = 0$ ， $x_{2} = 3$

查看试题解析
2. 将抛物线 $y = 2 x^{2} + 1$ 向左平移2个单位，向上平移 $3$ 个单位后得到的抛物线表达式为（）

A、 $y = 2 {(x - 2)}^{2} + 4$ B、 $y = 2 {(x + 2)}^{2} + 4$ C、 $y = 2 {(x - 2)}^{2} - 2$ D、 $y = 2 {(x + 2)}^{2} - 2$

查看试题解析
3. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $s i n A = \frac{5}{13}$ ，则 $c o s A$ 的值为（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{12}{13}$ D、 $\frac{13}{12}$

查看试题解析
4. 如图， $△ A B C$ 和 $△ A B C$ 是以点 $O$ 为位似中心的位似图形，若 $O A ： O A^{^{'}} = 1 ： 2$ ，则 $△ A B C$ 与 $△ A B C$ 的周长比为（）

A、 $1 ： 4$ B、 $1 ： 3$ C、 $1 ： 2$ D、 $1 ： 9$

查看试题解析
5. 某超市一月份的营业额为50万元，到三月底营业额累计为500万元．如果设平均每月的增长率为 $x$ ，依题意得，可列出方程为（）

A、 $50 {(1 + x)}^{2} = 500$ B、 $50 {(1 + x)}^{3} = 500$ C、 $50 {(1 + x)}^{2} = 450$ D、 $50 + 50 (1 + x) + 50 {(1 + x)}^{2} = 500$

查看试题解析
6. 如图，直线 $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线 $a$ ， $b$ 与这三条直线分别交于点 $A$ ， $B$ ， $C$ 和点 $E$ ， $F$ ， $F$ ，若 $A B ： B C = 5 ： 3$ ，则 $E F ： D F$ 等于（）

A、 $3 ： 8$ B、 $5 ： 8$ C、 $3 ： 5$ D、 $8 ： 11$

查看试题解析
7. 点 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (3 ， y_{3})$ 在反比例函数 $y = \frac{- 3}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{2} > y_{3} > y_{1}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{2} > y_{2} > y_{1}$ D、 $y_{3} > y_{1} > y_{2}$

查看试题解析
8. 某三棱柱的三种视图如图所示，已知俯视图中 $t a n B = \frac{1}{2}$ ， $S_{△ A B C} = 7$ ，下列结论中：①主视图中 $m = 3$ ；②左视图矩形的面积为 $18$ ；③俯视图 $∠ C$ 的正切值为 $\frac{2}{3}$ ．其中正确的个数为（）

A、 $3$ 个 B、 $2$ 个 C、 $1$ 个 D、 $0$ 个

查看试题解析
9. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = 1$ ，与 $x$ 轴的一个交点坐标为 $A (3 ， 0)$ ，其部分图象如图所示，下列结论中：① $a b c < 0$ ；② $b^{2} - 4 a c > 0$ ；③抛物线与 $x$ 轴的另一个交点的坐标为 $(- 1 ， 0)$ ；④方程 $a x^{2} + b x + c = 1$ 有两个不相等的实数根．其中正确的个数为（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $A B = 5$ ，点 $E$ 是 $B C$ 上一点，将 $△ A B E$ 沿直线 $A E$ 折叠，点 $B$ 落在矩形 $A B C D$ 的内部点 $F$ 处，若 $t a n ∠ D A F = \frac{3}{4}$ ，则 $B E$ 的长为（）

A、 $\frac{5}{2}$ B、 $\frac{3}{2}$ C、 $2$ D、 $\frac{9}{4}$

查看试题解析

二、填空题

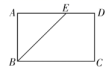
11. 若α是锐角且sinα= $\frac{\sqrt{3}}{2}$ ，则α的度数是．

查看试题解析
12. 一个盒子中装有标号为 $1$ ， $2$ ， $3$ ， $4$ 的四个小球，这些球除标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于 $5$ 的概率为．

查看试题解析
13. 我们把宽与长的比为黄金比 $(\frac{\sqrt{5} - 1}{2})$ 的矩形称为黄金矩形，如图，在黄金矩形 $A B C D$ 中， $A B < B C$ ， $B C = 2$ ， $∠ A B C$ 的平分线交 $A D$ 边于点 $E$ ，则 $D E$ 的长为．

查看试题解析
14. 如图，有一矩形养鸡场，养鸡场的一边靠墙（墙足够长），另三边用 $16$ 米的长篱笆围成，则矩形 $A B C D$ 面积的最大值是平方米．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = 14$ ， $A C = 10$ ，点 $D$ 是 $B C$ 上一点，点 $M$ 是 $B A$ 延长线上一点，已知 $t a n ∠ C A M = \frac{4}{3}$ ， $∠ D A B = 45 °$ ，则 $A D$ 的长为．

查看试题解析

三、解答题

16.

(1)、计算 $\sqrt{2} s i n 45 ° + 2 c o s 30 ° + | 1 - t a n 60 ° |$ ．

(2)、解方程： ${(x + 3)}^{2} = 2 x + 6$ ．

查看试题解析
17. 如图，在 $▱ A B C D$ 中，对角线 $A C$ 的垂直平分线分别交 $A D$ ， $B C$ 于点 $E$ ， $F$ ， $E F$ 与 $A C$ 相交于点 $O$ ，连接 $A F$ ， $C E$ ．

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、已知 $s i n ∠ A C F = \frac{\sqrt{5}}{5}$ ， $C F = 5$ ， $A B = 6$ ，请你写出 $s i n B$ 的值．

查看试题解析

18. 某“综合与实践”小组开展了测量运城北站关公铜像高度的实践活动，他们设计了两个测量方案如下表．经过老师与小组利用课余时间实地考察放弃了方案一，采用了方案二，他们在铜像底部所在的平地上选取两个不同的测点，分别测量了铜像顶端的仰角以及这两个测点之间的距离．为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果填入表格，测量数据如下表．

课题		测量公关铜像的高度
成员		组长：×××，组员：×××，×××，×××
工具		侧倾器，皮尺等
设计方案	方案一测量示意图		说明：线段 $A B$ 表示铜像，线段 $C D$ 表示侧倾器， $C D$ 的高度为 $1.1$ 米，点 $E$ 在 $A B$ 上，点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 在同一平面内．需要测量的数据有 $B C$ 的距离，倾斜角 $B C$ 的距离，倾斜角 $∠ A D E$ 的度数．
	方案二测量示意图		说明：线段 $A B$ 表示铜像，线段 $C D$ ， $E G$ 表示侧倾器， $C D$ ， $F G$ 的高度为 $1.1$ 米，点 $E$ 在 $A B$ 上，点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ ， $G$ 在同一平面内．需要测量的数据有 $C F$ 的距离，倾斜角 $∠ A D E$ ， $∠ A G E$ 的度数．
实施方案	方案二的测量数据	$∠ A D E$ 的平均值	$∠ A G E$ 的平均值	$C F$ 的平均值
		$28.5 °$	$45 °$	$10$ 米

(1)、“综合与实践”小组为什么放弃方案一，你认为原因可能是什么？（写出一条即可）

(2)、请你根据他们的测量数据计算公关铜像的高度．

（参考数据： $s i n 28.5 ° \approx 0.48$ ， $c o s 28.5 ° \approx 0.88$ ， $t a n 28.5 ° \approx \frac{6}{11}$ ）

查看试题解析

19. 如图，一次函数 $y_{1} = x + b$ 与反比例函数 $y_{2} = \frac{k}{x}$ 交于点 $A (1 ， a)$ ， $D (- 4 ， - 1)$ ，与 $y$ 轴， $x$ 轴分别交于点 $B$ ， $C$ ．

(1)、求反比例函数的表达式；

(2)、作 $A E ⊥ y$ 轴于点 $E$ ，连接 $D E$ ，求 $△ A D E$ 的面积；

(3)、根据图象请直接写出当 $y_{1} > y_{2}$ 时， $x$ 的取值范围．

查看试题解析
20. 某经销商经销一种封面为建党 $100$ 周年的笔记本，每本进价为 $3$ 元，按每本 $5$ 元出售，每天可售出 $30$ 本．调查发现这种笔记本销售单价每提高 $1$ 元，每天的销售量就会减少 $3$ 本．

(1)、当销售单价定为多少元时，该经销商每天销售这笔记本的销售利润为 $105$ 元？

(2)、当销售单价定为多少元时，才能使该经销商每天销售这种笔记本所得的利润最大？最大利润是多少元？

查看试题解析
21. 阅读与思考
阅读以下材料，并按要求完成相应的任务：
学习了反比例函数的性质后，希望学习小组又进行了深入的探究，发现：如果在双曲线上任取两点，过这两点分别向两坐标轴垂线（垂足不同时在 $x$ 或 $y$ 轴上），那么垂足的连线和这两点的连线平行．如图1，点 $A$ ， $B$ 是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限图象上的两点，作 $A D ⊥ y$ 轴于点 $D$ ， $B C ⊥ x$ 轴于点 $C$ ，连接 $C D$ ，则 $A B ∥ C D$ ；如图2，点 $A$ ， $B$ 是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限图象上的两点，作 $A D ⊥ x$ 轴于点 $D$ ， $D$ ， $B C ⊥ y$ 轴于点 $C$ ，连接 $C D$ ，则 $A B ∥ C D$ ．在老师指导下希望学习小组进行严格推理，证明这一结论是正确的．
（结论应用）

(1)、任务：如图2，若 $A D$ 与 $B C$ 交于点 $E$ ， $C E ： B E = 1 ： 2$ ．
① $\frac{C D}{A B}$ 的值为．
②若 $△ A B E$ 的面积为 $6$ ，则四边形 $O C E D$ 的面积为．

(2)、智慧学习小组利用上述结论又进行了新的探究，如图3，直线 $E F$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于 $A$ ， $B$ 两点，点 $A$ 在点 $B$ 的上方，与 $x$ ， $y$ 轴分别交于点 $E$ ， $F$ ，则得到 $A E = B F$ 这一结论．
下面是该结论的部分证明：
证明：作 $A D ⊥ y$ 轴于点 $D$ ， $B C ⊥ x$ 轴于点 $C$ ，连接 $C D$ ，则 $A B ∥ C D$ ， $B C ∥ D E$ ．
$∴ ∠ D E A = ∠ C B F$ ，四边形 $E D C B$ 是平行四边形．
……
仔细阅读上面的证明过程，按照上面的证明思路，请你补充完整．

查看试题解析
22. 综合与实践
如图1，在综合实践课上，老师让学生用两个等腰直角三角形进行图形的旋转探究．在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，在 $R t △ A M N$ 中， $∠ M A N = 90 °$ ， $A M = A N$ ，点 $M$ ， $N$ 分别在 $A C$ ， $A B$ 边行，直角顶点重合在一起，将 $R t △ A M N$ 绕点 $A$ 逆时针旋转，设旋转角 $∠ M A C = α$ ，其中 $0 ° < α < 90 °$ ．

(1)、当点 $M$ 落在 $B C$ 上时，如图2：
①请直接写出 $∠ B M N$ 的度数为 ▲ （用含 $α$ 的式子表示）；
②若 $t a n α = \frac{3}{4}$ ， $A C = 7$ ，求 $A M$ 的长；

(2)、如图3，连接 $B N$ ， $C M$ ，并延长 $C M$ 交 $B N$ 于点 $E$ ，请判断 $C E$ 与 $B N$ 的位置关系，并加以证明；

(3)、如图4，当 $∠ B A C$ 与 $∠ M A N$ 是两个相等钝角时，其他条件不变，即在 $△ A B C$ 与 $△ A M N$ 中， $A B = A C$ ， $A M = A N$ ， $∠ M A N = ∠ B A C = β$ ， $∠ M A C = α$ ，则 $∠ C E N$ 的度数为（用含 $α$ 或 $β$ 的式子表示）．

查看试题解析
23. 综合与探究
如图，直线 $y = - \frac{2}{3} x + 4$ 与 $x$ 轴， $y$ 轴分别交于 $B$ ， $C$ 两点，抛物线 $y = a x^{2} + \frac{4}{3} x + c$ 经过 $B$ ， $C$ 两点，与 $x$ 轴的另一个交点为 $A$ （点 $A$ 在点 $B$ 的左侧），抛物线的顶点为点 $D$ ．抛物线的对称轴与 $x$ 轴交于点 $E$ ．

(1)、求抛物线的表达式及顶点 $D$ 的坐标；

(2)、点M是线段 $B C$ 上一动点，连接 $D M$ 并延长交 $x$ 轴交于点 $F$ ，当 $F M ： F D = 1 ： 4$ 时，求点 $M$ 的坐标；

(3)、点 $P$ 是该抛物线上的一动点，设点 $P$ 的横坐标为 $m$ ，试判断是否存在这样的点 $P$ ，使 $∠ P A B + ∠ B C O = 90 °$ ，若存在，请直接写出 $m$ 的值；若不存在，请说明理由．

查看试题解析