黑龙江省绥化市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 下列图形既是中心对称又是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,粮仓可以近似地看作由圆锥和圆柱组成,其主视图是( )
2. 如图,粮仓可以近似地看作由圆锥和圆柱组成,其主视图是( )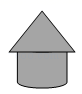 A、
A、 B、
B、 C、
C、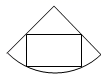 D、
D、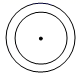 3. 下列事件中是必然事件的是( )A、抛掷一枚质地均匀的硬币,正面朝上 B、随意翻到一本书的某页,这一页的页码是偶数 C、打开电视机,正在播放广告 D、从两个班级中任选三名学生,至少有两名学生来自同一个班级4. 在六张卡片上分别写有6, ,3.1415, ,0, 六个数,从中随机抽取一张,卡片上的数为无理数的概率是( )A、 B、 C、 D、5. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )
3. 下列事件中是必然事件的是( )A、抛掷一枚质地均匀的硬币,正面朝上 B、随意翻到一本书的某页,这一页的页码是偶数 C、打开电视机,正在播放广告 D、从两个班级中任选三名学生,至少有两名学生来自同一个班级4. 在六张卡片上分别写有6, ,3.1415, ,0, 六个数,从中随机抽取一张,卡片上的数为无理数的概率是( )A、 B、 C、 D、5. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )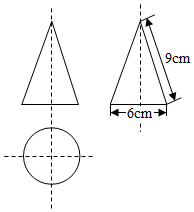 A、 B、 C、 D、6. 的值等于( )A、 B、 C、 D、17. 如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米, ,则缆车从A点到达B点,上升的高度(BC的长)为( )
A、 B、 C、 D、6. 的值等于( )A、 B、 C、 D、17. 如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米, ,则缆车从A点到达B点,上升的高度(BC的长)为( )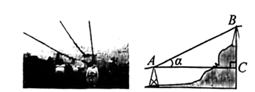 A、 米 B、 米 C、 米 D、 米8. 已知反比例函数 ,则下列描述错误的是( )A、图象位于第一,第三象限 B、图象必经过点 C、图象不可能与坐标轴相交 D、 随 的增大而减小9. 如图,直线 ,直线 和 被 , , 所截, , , ,则 的长为( )
A、 米 B、 米 C、 米 D、 米8. 已知反比例函数 ,则下列描述错误的是( )A、图象位于第一,第三象限 B、图象必经过点 C、图象不可能与坐标轴相交 D、 随 的增大而减小9. 如图,直线 ,直线 和 被 , , 所截, , , ,则 的长为( )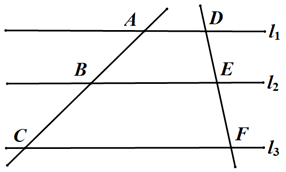 A、2 B、3 C、4 D、10. 由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体的个数最多为( )
A、2 B、3 C、4 D、10. 由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体的个数最多为( )
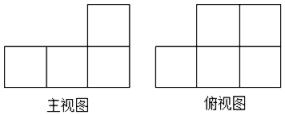 A、7个 B、8个 C、9个 D、10个11. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2 , 则四边形BDEC的面积为( )
A、7个 B、8个 C、9个 D、10个11. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2 , 则四边形BDEC的面积为( ) A、12cm2 B、9cm2 C、6cm2 D、3cm212. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ,④ ,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )
A、12cm2 B、9cm2 C、6cm2 D、3cm212. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ,④ ,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )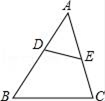 A、①②④ B、②④⑤ C、①②③④ D、①②③⑤
A、①②④ B、②④⑤ C、①②③④ D、①②③⑤二、填空题
-
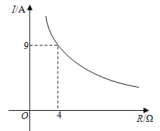
13. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为Ω.
 14. 一个不透明的袋子装有除颜色外其余均相同的2个红球和m个黄球,随机从袋中摸出个球记录下颜色,再放回袋中摇匀大量重复试验后,发现摸出红球的频率稳定在0.2附近,则m的值为 .15. 如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是 .
14. 一个不透明的袋子装有除颜色外其余均相同的2个红球和m个黄球,随机从袋中摸出个球记录下颜色,再放回袋中摇匀大量重复试验后,发现摸出红球的频率稳定在0.2附近,则m的值为 .15. 如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是 . 16. 如图,在矩形 中, ,垂足为点 .若 , ,则 的长为.
16. 如图,在矩形 中, ,垂足为点 .若 , ,则 的长为.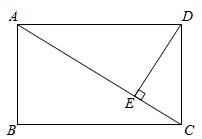 17. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.
17. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.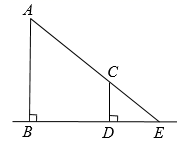 18. 如图,点A在曲线到上,点B在双曲线上,ABx轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值为 .
18. 如图,点A在曲线到上,点B在双曲线上,ABx轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值为 . 19. 在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是 .20. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至D,使BD=AB,连接AD,得∠D=15°,所以tan15°2 . 类比这种方法,计算tan22.5°的值为 .
19. 在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是 .20. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至D,使BD=AB,连接AD,得∠D=15°,所以tan15°2 . 类比这种方法,计算tan22.5°的值为 . 21. 贵阳市2021年中考物理实验操作技能测试中,要求学生两人一组合作进行,并随机抽签决定分组.有甲、乙、丙、丁四位同学参加测试,则甲、乙两位同学分到同一组的概率是.22. 如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP= .
21. 贵阳市2021年中考物理实验操作技能测试中,要求学生两人一组合作进行,并随机抽签决定分组.有甲、乙、丙、丁四位同学参加测试,则甲、乙两位同学分到同一组的概率是.22. 如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP= .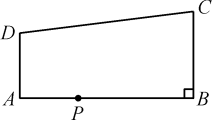
三、解答题
-
23. 如图所示的平面直角坐标系中, 的三个顶点坐标分别为 ,请按如下要求画图:

( 1 )以坐标原点O为旋转中心,将 顺时针旋转90°,得到 ,请画出 ;
( 2 )以坐标原点O为位似中心,在x轴下方,画出 的位似图形 ,使它与 的位似比为 .
24. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄始终平分同一平面内两条伞骨所成的角 , 且 , 从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点的位置,且A,B,三点共线, , B为中点,当时,伞完全张开. (1)、求的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据:)25. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)、求的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据:)25. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.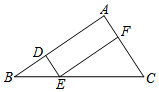 (1)、求证:△BDE∽△EFC.(2)、设 ,
(1)、求证:△BDE∽△EFC.(2)、设 ,①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
26. 如图,一次函数的图象 与反比例函数 的图象在第一象限交于点 ,与y轴的负半轴交于点B,且 .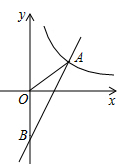 (1)、求一次函数 与反比例函数 的表达式;(2)、已知点C在x轴上,且 的面积是8,求此时点C的坐标;(3)、请直接写出不等式 的解集.27. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当 和 时,图象是线段;当 时,图象是反比例函数的一部分.
(1)、求一次函数 与反比例函数 的表达式;(2)、已知点C在x轴上,且 的面积是8,求此时点C的坐标;(3)、请直接写出不等式 的解集.27. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当 和 时,图象是线段;当 时,图象是反比例函数的一部分.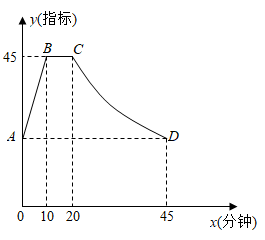 (1)、求点A对应的指标值;(2)、张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.28. 如图,△ABC内接于⊙O,D是⊙O的直径AB的延长线上一点,∠DCB=∠OAC.过圆心O作BC的平行线交DC的延长线于点E.
(1)、求点A对应的指标值;(2)、张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.28. 如图,△ABC内接于⊙O,D是⊙O的直径AB的延长线上一点,∠DCB=∠OAC.过圆心O作BC的平行线交DC的延长线于点E. (1)、求证:CD是⊙O的切线;(2)、若CD=4,CE=6,求⊙O的半径及tan∠OCB的值.29. 如图所示,抛物线与x轴交于A、B两点,与y轴交于点C,且 , , , 抛物线的对称轴与直线BC交于点M,与x轴交于点N.
(1)、求证:CD是⊙O的切线;(2)、若CD=4,CE=6,求⊙O的半径及tan∠OCB的值.29. 如图所示,抛物线与x轴交于A、B两点,与y轴交于点C,且 , , , 抛物线的对称轴与直线BC交于点M,与x轴交于点N. (1)、求抛物线的解析式;(2)、若点P是对称轴上的一个动点,是否存在以P、C、M为顶点的三角形与相似?若存在,求出点P的坐标,若不存在,请说明理由.(3)、D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到抛物线对称轴上的点F,最后返回到点C.要使动点G走过的路程最短,请找出点E、F的位置,写出坐标,并求出最短路程.
(1)、求抛物线的解析式;(2)、若点P是对称轴上的一个动点,是否存在以P、C、M为顶点的三角形与相似?若存在,求出点P的坐标,若不存在,请说明理由.(3)、D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到抛物线对称轴上的点F,最后返回到点C.要使动点G走过的路程最短,请找出点E、F的位置,写出坐标,并求出最短路程.