广东省广州市黄埔区2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-02-13 类型：期末考试
一、单选题
-
1. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 函数y＝x2+x﹣2的图象与y轴的交点坐标是（ ）A、（﹣2，0） B、（1，0） C、（0，﹣2） D、（0，2）3. 平面内有两点P，O，⊙O的半径为5，若PO＝4，则点P与⊙O的位置关系是（ ）A、圆内 B、圆上 C、圆外 D、圆上或圆外4. 下列函数中，y是关于x的反比例函数的是（ ）A、y＝﹣3x+6 B、y=x2 C、y＝ D、y＝5. 下列式子为一元二次方程的是（ ）A、5x2﹣1 B、4a2＝81 C、 D、（3x﹣2）（x+1）＝8y﹣36. 下列事件是必然事件的为（ ）A、购买一张体育彩票， 中奖 B、经过有交通信号灯的路口， 遇到红灯 C、2022 年元旦是晴天 D、在地面上向空中抛掷一石块， 石块终将落下7. 下列各点中，关于原点对称的两个点是（ ）A、（﹣5，0）与（0，5） B、（0，2）与（2，0） C、（﹣2，﹣1）与（﹣2，1） D、（2，﹣1）与（﹣2，1）8. 下列是对方程2x2﹣2x+1＝0实根情况的判断，正确的是（ ）A、有两个不相等的实数根 B、有一个实数根 C、有两个相等的实数根 D、没有实数根9. 如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（ ）
A、AB=AD B、BC=CD C、 D、∠BCA=∠DCA10. 正比例函数 与反比例函数 的图象相交于A，C两点，AB⊥x轴于点B，CD⊥x轴于点D（如图），则四边形ABCD的面积为（ ）
A、1 B、 C、2 D、二、填空题
-
11. 方程x2﹣3x+2＝0两个根的和为 ， 积为 ．12. 在一个暗箱里放入除颜色外其它都相同的1个红球和11个黄球，搅拌均匀后随机任取一球，取到红球的概率是 ．13. 直线y＝x+2关于原点中心对称的直线的方程为 ．14. 把一副普通扑克牌中的13张黑桃牌洗匀后正面朝下放在桌子上，从中随机抽取一张，则抽出的牌上的数小于5的概率为 ．15. 在⊙O中，圆心角∠AOC＝120°，则⊙O内接四边形ABCD的内角∠ABC＝ ．
16. 如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=2，⊙C的半径为1，点P是斜边AB上的点，过点P作⊙C的一条切线PQ（点Q是切点），则线段PQ的最小值为 ．
三、解答题
-
17. 如图，在方格纸中，已知顶点在格点处的△ABC，请画出将△ABC绕点C旋转180°得到的△A'B'C'．（需写出△A'B'C'各顶点的坐标）．
18. 解方程：x2+1＝4﹣2x．19. 已知二次函数y＝ax2+bx+c的图象与y轴相交于点A，y与x的部分对应值如表：x
﹣1
0
1
2
3
y
0
■
﹣4
﹣3
0
(1)、直接写出抛物线的开口方向，对称轴，顶点坐标及点A的坐标；(2)、在给出的坐标系中画出该函数图象的草图．20. 如图，AB、CD是⊙O的两条弦，＝ ， OE⊥AB，OF⊥CD，垂足分别为E、F．求证：OE＝OF．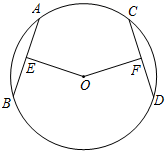
21. 一个不透明的口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4随机摸取一个小球后，不放回，再随机摸出一个小球，分别求下列事件的概率：(1)、两次取出的小球标号和为奇数；(2)、两次取出的小球标号和为偶数．22. 参加足球联赛的每两队之间都进行两场比赛．共要比赛90场．共有多少个队参加比赛？23. 如图所示，已划A（﹣1，0），B（0，1），直线AB与反比例函数y＝（m≠0）的图象在第一象限交于C点，CD垂置于x轴，垂足为D，且OD＝1．
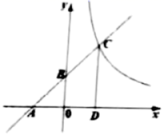(1)、当y＝1时，求反比例函数y＝对应x的值；(2)、当1＜y＜4时，求反比例函数y＝对应x的取值范围．24. 如图，AB、CD是⊙O中两条互相垂直的弦，垂足为点E，且AE＝CE，点F是BC的中点，延长FE交AD于点G，已知AE＝1，BE＝3，OE＝ ．
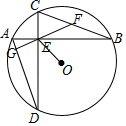(1)、求证：△AED≌△CEB；(2)、求证：FG⊥AD；(3)、若一条直线l到圆心O的距离d＝ ， 试判断直线l是否是圆O的切线，并说明理由．25. 如图，抛物线y＝mx2﹣4mx﹣5m（m＞0）与x轴交于A，B两点，与y轴交于C点．
(1)、求抛物线顶点M的坐标（用含m的代数式表示），A，B两点的坐标；(2)、证明△BCM与△ABC的面积相等；(3)、是否存在使△BCM为直角三角形的抛物线？若存在，请求出；若不存在，请说明理由．