广东省东莞市十校联考2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 下列图形,可以看作中心对称图形的是( )A、
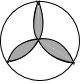 B、
B、 C、
C、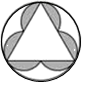 D、
D、 2. 由于新冠疫情影响,某口罩加工厂改进技术,扩大生产,从今年10月份开始,平均每个月生产量的增长率为x.已知今年10月份的生产量为800万个,12月的生产量为1152万个,则可列方程( )A、800+800x2=1152 B、800(1+x)2=1152 C、800+800(1+x)+800(1+x)2=1152 D、800+800(1+x)=11523. 将抛物线y=(x﹣1)2+2向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、y=(x﹣1)2+5 B、y=(x+2)2+6 C、y=(x﹣4)2+6 D、y=(x﹣3)2+54. 如图,ABC中,∠ACB=90°,∠ABC=40°.将ABC绕点B逆时针旋转得到 , 使点C的对应点恰好落在边AB上,则的度数是( )
2. 由于新冠疫情影响,某口罩加工厂改进技术,扩大生产,从今年10月份开始,平均每个月生产量的增长率为x.已知今年10月份的生产量为800万个,12月的生产量为1152万个,则可列方程( )A、800+800x2=1152 B、800(1+x)2=1152 C、800+800(1+x)+800(1+x)2=1152 D、800+800(1+x)=11523. 将抛物线y=(x﹣1)2+2向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、y=(x﹣1)2+5 B、y=(x+2)2+6 C、y=(x﹣4)2+6 D、y=(x﹣3)2+54. 如图,ABC中,∠ACB=90°,∠ABC=40°.将ABC绕点B逆时针旋转得到 , 使点C的对应点恰好落在边AB上,则的度数是( ) A、50° B、70° C、110° D、120°5. 如图,在中, , 则的长为( ).
A、50° B、70° C、110° D、120°5. 如图,在中, , 则的长为( ). A、 B、8 C、10 D、166. 如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( )
A、 B、8 C、10 D、166. 如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( )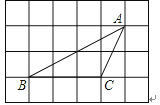 A、 B、 C、 D、7. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
A、 B、 C、 D、7. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )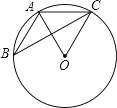 A、30° B、45° C、60° D、70°8. 东莞市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,操控者和教学楼BC的距离为60米,则教学楼BC的高度是( )米.
A、30° B、45° C、60° D、70°8. 东莞市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,操控者和教学楼BC的距离为60米,则教学楼BC的高度是( )米. A、 B、 C、 D、9. 如图,二次函数y=ax2+bx+c与反比例函数y=的图象相交于点A(﹣1,y1)、B(1,y2)、C(3,y3)三个点,则不等式ax2+bx+c>的解集是( )
A、 B、 C、 D、9. 如图,二次函数y=ax2+bx+c与反比例函数y=的图象相交于点A(﹣1,y1)、B(1,y2)、C(3,y3)三个点,则不等式ax2+bx+c>的解集是( ) A、﹣1<x<0或1<x<3 B、x<﹣1或1<x<3 C、﹣1<x<0或x>3 D、﹣1<x<0或0<x<110. 如图,RtABC中,∠C=90°,∠A=30°,BC= , 作∠ABC的平分线BE交CA于点F,以点B为圆心,以BF为长度作弧,交BA于点G,则阴影部分的面积为( )
A、﹣1<x<0或1<x<3 B、x<﹣1或1<x<3 C、﹣1<x<0或x>3 D、﹣1<x<0或0<x<110. 如图,RtABC中,∠C=90°,∠A=30°,BC= , 作∠ABC的平分线BE交CA于点F,以点B为圆心,以BF为长度作弧,交BA于点G,则阴影部分的面积为( ) A、 B、 C、 D、11. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数的图象上,则经过点B的反比例函数中k的值是( )
A、 B、 C、 D、11. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数的图象上,则经过点B的反比例函数中k的值是( ) A、﹣2 B、﹣4 C、﹣3 D、﹣112. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c>0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2;⑤3a+c<0.其中正确结论的个数是( )
A、﹣2 B、﹣4 C、﹣3 D、﹣112. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c>0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2;⑤3a+c<0.其中正确结论的个数是( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. 已知一元二次方程x2-4x-3=0的两根分别为x1 , x2 , 则x1+x2= .14. 边长为2的正三角形的外接圆的半径等于 .15. 若点(m,0)在二次函数y=x2﹣3x+2的图象上,则2m2﹣6m+2029的值为 .16. 如图,ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,CD=6,OA交BC于点E,则AD的长度是 .
 17. 如图,在平行四边形中, , , 垂足为E, , 连接 , 若 , 则 .
17. 如图,在平行四边形中, , , 垂足为E, , 连接 , 若 , 则 . 18. 如图,OA1B1 , A1A2B2 , A2A3B3 , ⋯是分别以A1 , A2 , A3 , …,为直角顶点且一条直角边在x轴正半轴上的等腰直角三角形,其斜边中点C1(x1 , y1),C2(x2 , y2),C3(x3 , y3),…,均在反比例函数的图象上,则C1的坐标是_;y1+y2+y3+…+y2022的值为 .
18. 如图,OA1B1 , A1A2B2 , A2A3B3 , ⋯是分别以A1 , A2 , A3 , …,为直角顶点且一条直角边在x轴正半轴上的等腰直角三角形,其斜边中点C1(x1 , y1),C2(x2 , y2),C3(x3 , y3),…,均在反比例函数的图象上,则C1的坐标是_;y1+y2+y3+…+y2022的值为 .
三、解答题
-
19.(1)、解方程: ,(2)、计算:20. 东莞某镇斥资打造夜市网红街,王阿姨在这夜市做起了地摊生意,他以每件40元的价格购进一种商品,在销售过程中发现这种商品每天的销售量y(件)与每件的销售单价x(元)满足一次函数关系:y=﹣2x+140(x>40).(1)、若设每天的利润为w元,请求出w与x的函数关系式;(2)、若每天的销售量不少于44件,则销售单价定为多少元时,此时利润最大,最大利润是多少?21. 如图,直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=(x<0)交于点A(﹣1,n),连接OA.
 (1)、求直线与双曲线的解析式;(2)、求OAC的面积;(3)、求∠OAB的正弦值.22. 如图,将边长为4的正方形纸片ABCD折叠,使点A落在边CD上的点M处(不与点C、D重合),连接AM,折痕EF分别交AD、BC、AM于点E、F、H,边AB折叠后交边BC于点G.
(1)、求直线与双曲线的解析式;(2)、求OAC的面积;(3)、求∠OAB的正弦值.22. 如图,将边长为4的正方形纸片ABCD折叠,使点A落在边CD上的点M处(不与点C、D重合),连接AM,折痕EF分别交AD、BC、AM于点E、F、H,边AB折叠后交边BC于点G.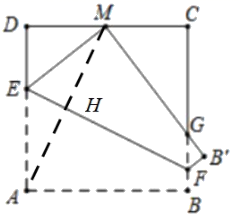 (1)、求证:EDM∽MCG;(2)、若DM=CD,求CG的长;(3)、若点M是边CD上的动点,四边形CDEF的面积S是否存在最值?若存在,求出这个最值;若不存在,说明理由.23. 如图,在RtABC中,∠ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点E,连接DE、DP.点F为线段CP上一点,连接DF,∠FDP=∠DEP.
(1)、求证:EDM∽MCG;(2)、若DM=CD,求CG的长;(3)、若点M是边CD上的动点,四边形CDEF的面积S是否存在最值?若存在,求出这个最值;若不存在,说明理由.23. 如图,在RtABC中,∠ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点E,连接DE、DP.点F为线段CP上一点,连接DF,∠FDP=∠DEP. (1)、求证:DF是⊙O的切线;(2)、当时,求证AB=AP;(3)、当AB=15,BC=20时,是否存在点P,使得BDE是以BD为腰的等腰三角形,若存在,求出所有符合条件的CP的长;若不存在,请说明理由.24. 如图,直线y=x+2与x轴,y轴分别交于点A,C,抛物线y=﹣+bx+c经过A,C两点,与x轴的另一交点为B,点D是抛物线上一动点.
(1)、求证:DF是⊙O的切线;(2)、当时,求证AB=AP;(3)、当AB=15,BC=20时,是否存在点P,使得BDE是以BD为腰的等腰三角形,若存在,求出所有符合条件的CP的长;若不存在,请说明理由.24. 如图,直线y=x+2与x轴,y轴分别交于点A,C,抛物线y=﹣+bx+c经过A,C两点,与x轴的另一交点为B,点D是抛物线上一动点.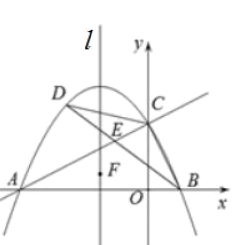 (1)、求抛物线的解析式;(2)、在对称轴直线l上有一点P,连接CP,BP,则CP+BP的最小值为;(3)、当点D在直线AC上方时,连接BC,CD,BD,BD交AC于点E,令CDE的面积为S1 , BCE的面积为S2 , 求的最大值;(4)、点F是该抛物线对称轴l上一动点,是否存在以点B,C,D,F为顶点的平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在对称轴直线l上有一点P,连接CP,BP,则CP+BP的最小值为;(3)、当点D在直线AC上方时,连接BC,CD,BD,BD交AC于点E,令CDE的面积为S1 , BCE的面积为S2 , 求的最大值;(4)、点F是该抛物线对称轴l上一动点,是否存在以点B,C,D,F为顶点的平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.