北京市密云区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 如果4m=5n（n≠0），那么下列比例式成立的是（）

A、 $\frac{m}{4} = \frac{n}{5}$ B、 $\frac{m}{5} = \frac{n}{4}$ C、 $\frac{m}{n} = \frac{4}{5}$ D、 $\frac{m}{4} = \frac{5}{n}$

查看试题解析
2. 已知⊙O的半径为4，点P 在⊙O外部，则OP需要满足的条件是（）

A、OP>4 B、0≤OP<4 C、OP>2 D、0≤OP<2

查看试题解析
3. 抛物线 $y = {(x - 1)}^{2} + 2$ 的对称轴是（）

A、直线x＝－1 B、直线x＝1 C、直线x＝－2 D、直线x＝2

查看试题解析
4. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $B C = 4$ ，则 $\tan A$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
5. 如图，身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时，发现自己在地面上的影子CE的长是2米，则路灯AB的高为（）

A、5米 B、6.4米 C、8米 D、10米

查看试题解析
6. 如图，在⊙O中，C、D为⊙O上两点，AB是⊙O的直径，已知∠AOC=130°，则∠BDC的度数为（）

A、65° B、50° C、30° D、25°

查看试题解析
7. 如图所示的网格是正方形网格，A，B，C，D，E，F是网格线的交点，则△ABC的面积与△DEF的面积比为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、2 D、4

查看试题解析
8. 如图，一个矩形的长比宽多3cm，矩形的面积是Scm² ．设矩形的宽为xcm，当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（）

A、S=4x+6 B、S=4x-6 C、S=x²+3x D、S=x²-3x

查看试题解析

二、填空题

9. 若cosA $= \frac{\sqrt{2}}{2}$ ，则锐角A的度数为．

查看试题解析
10. 点A（2，y₁），B（3，y₂）是反比例函数 $y = - \frac{12}{x}$ 图象上的两点，那么y₁ ， y₂的大小关系是y₁y₂ ．（填“＞”，“＜”或“=”）

查看试题解析
11. 如图，正六边形ABCDEF内接于⊙O，若⊙O的周长为8π，则正六边形的边长为．

查看试题解析
12. 请写出一个开口向上，并且与y轴交于点（0，-5）的抛物线的表达式．

查看试题解析
13. 一个扇形的圆心角为120°，半径为3，则这个扇形的面积为（结果保留π）

查看试题解析
14. 如图1是一种手机平板支架，图2是其侧面结构示意图．托板AB固定在支撑板顶端的点C处，托板AB可绕点C转动，支撑板CD可绕点D转动．如图2，若量得支撑板长CD=8cm，∠CDE=60°，则点C到底座DE的距离为cm（结果保留根号）．

查看试题解析
15. 如图， $P A ， P B$ 是 $⊙ O$ 的切线， $A ， B$ 是切点．若 $∠ P = 50 °$ ，则 $∠ A O B =$ ．

查看试题解析
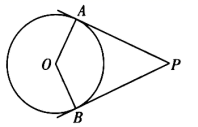16. 如图，抛物线y=-x²+2．将该抛物线在x轴和x轴上方的部分记作C₁ ，将x轴下方的部分沿x轴翻折后记作C₂ ， C₁和C₂构成的图形记作C₃ ．关于图形C₃ ，给出如下四个结论：①图形C₃关于y轴成轴对称；② 图形C₃有最小值，且最小值为0；③ 当x>0时，图形C₃的函数值都是随着x的增大而增大的；④ 当-2≤x≤2时，图形C₃恰好经过5个整点（即横、纵坐标均为整数的点）．以上四个结论中，所有符合题意结论的序号是．

查看试题解析

三、解答题

17. 计算： $\sqrt{8} - {(π - \sqrt{2})}^{0} - 2 c o s 45 ° + | - 4 |$ ．

查看试题解析
18. 下面是小玟同学设计的“作一个角等于已知角”的尺规作图过程．
已知：在△ABC中，AB=BC，BD平分∠ABC交AC于点D．
求作：∠BPC，使∠BPC=∠BAC．
作法：① 分别以点B和点C为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧交于点E和点F，
连接EF交BD于点O；
② 以点O为圆心，OB的长为半径作⊙O；
③ 在劣弧AB上任取一点P（不与点A、B重合），连接BP和CP．所以∠BPC=∠BAC．
根据小玟设计的尺规作图过程．

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接OA、OC．
∵AB=BC，BD平分∠ABC，
∴BD⊥AC且AD=CD．
∴OA=OC．
∵EF是线段BC的垂直平分线，
∴OB= ▲ ．
∴OB=OA．
∴⊙O为△ABC的外接圆．
∵点P在⊙O上，
∴∠BPC=∠BAC（ ▲ ）（填推理的依据）．

查看试题解析
19. 已知二次函数 $y = x^{2} - 4 x + 3$ ．

(1)、用配方法将其化为 $y = a {(x - h)}^{2} + k$ 的形式；

(2)、在所给的平面直角坐标系xOy中，画出它的图象．

查看试题解析
20. 已知：如图，在△ABC中，∠ABC=2∠C，BD平分∠ABC．求证：△ABD∽△ACB．

查看试题解析
21. 如图，在△ABC中，∠C = 90°， $s i n A = \frac{3}{5}$ ， D为AC上一点，∠BDC = 45°，CD=6．求AD的长．

查看试题解析
22. 如图，在平面直角坐标系xOy中的第一象限内，反比例函数的图象经过点A（4，1），点B（x，y）是该函数图象上的一个动点．

(1)、求反比例函数的表达式；

(2)、当y>1时，结合图象直接写出x的取值范围．

查看试题解析
23. 在平行四边形ABCD中，E为AB上一点，连接CE，F为CE上一点，且∠DFE=∠A．

(1)、求证：△DCF∽△CEB；

(2)、若BC=4，CE= $3 \sqrt{5}$ ， tan∠CDF= $\frac{1}{2}$ ，求线段BE的长．

查看试题解析
24. 从2020年3月开始，一群野生亚洲象从云南西双版纳傣族自治州走出丛林，一路北上，历经17个月迁徙逾500公里安全返回栖息地，引发国内外一波“观象热潮”．象群北移途经峨山县时，一头亚洲象曾脱离象群．如图，A，B，C分别表示峨山县、象群位置和独象位置．经测量，象群在峨山县西北方向约12公里处，独象位于象群的正东方向和峨山县北偏东30°方向的交汇处，请你计算此时独象距离象群多少公里？（结果保留根号）

查看试题解析
25. 如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD的外角∠DAF的平分线．

(1)、求证：AM是⊙O的切线；

(2)、连接CO并延长交AM于点N，若⊙O的半径为2，∠ANC = 30°，求CD的长．

查看试题解析
26. 在平面直角坐标系xOy中，关于x的二次函数y= $x^{2}$ -2ax+b与y轴相交于点（0，-3）．

(1)、当抛物线的图象经过点（1，-4）时，求该抛物线的表达式；

(2)、求这个二次函数的对称轴（用含a的式子表示）；

(3)、若抛物线上存在两点A（ $x_{1}$ ， $y_{1}$ ）和B（ $x_{2}$ ， $y_{2}$ ），其中 $x_{1}$ - $y_{1}$ =0， $x_{2}$ + $y_{2}$ =0．当 $x_{1}$ <0， $x_{2}$ >0时，总有 $x_{1}$ + $x_{2}$ >0，求a的取值范围．

查看试题解析
27. 如图，在正方形ABCD中，点E是CD边上一动点（点E与点C、D不重合），连接AE，过点A作AE的垂线交CB延长线于点F，连接EF．

(1)、依据题意，补全图形；

(2)、求∠AEF的度数；

(3)、连接AC交EF于点H，若 $\frac{F H}{E H} = a$ ，用含a的等式表示线段CF和CE之间的数量关系，并说明理由．

查看试题解析
28. 在平面直角坐标系xOy中，已知点A（1，0）和点B（5，0）．对于线段AB和直线AB外的一点C，给出如下定义：点C到线段AB两个端点的连线所构成的夹角∠ACB叫做线段AB关于点C的可视角，其中点C叫做线段AB的可视点．

(1)、在点D（-2，2）、E（1，4）、F（3，-2）中，使得线段AB的可视角为45°的可视点是；

(2)、⊙P为经过A，B两点的圆，点M是⊙P上线段AB的一个可视点.
①当AB为⊙P的直径时，线段AB的可视角∠AMB为度；
②当⊙P的半径为4时，线段AB的可视角∠AMB为度；

(3)、已知点N为y轴上的一个动点，当线段AB的可视角∠ANB最大时，求点N的坐标．

查看试题解析