上海市徐汇区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{p - 1}}$ B、 $\sqrt{12 y}$ C、 $\sqrt{x^{2} - 2 x + 1}$ D、 $\sqrt{13 a b}$

查看试题解析
2. 下列方程中，没有实数根的是（）

A、 $x^{2} - 3 x - 1 = 0$ B、 $x^{2} - 3 x = 0$ C、 $x^{2} - 2 x + 1 = 0$ D、 $x^{2} - 2 x + 3 = 0$

查看试题解析
3. 如果正比例函数图象与反比例函数图象的一个交点的坐标为（3，-4），那么另一个交点的坐标为（）

A、（-3，-4） B、（3，4） C、（−3，4） D、（-4，3）

查看试题解析
4. 满足下列条件的三角形中，不是直角三角形的是（）

A、三内角之比为3：4：5 B、三边长的平方之比为1：2：3 C、三边长之比为7：24：25 D、三内角之比为1：2：3

查看试题解析
5. 下列命题中，其逆命题是真命题的命题个数有（）
⑴全等三角形的对应边相等； ⑵对顶角相等；
⑶等角对等边； ⑷全等三角形的面积相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图所示，在平面直角坐标系xOy中，点A、B、C为反比例函数y= $\frac{k}{x}$ （k＞0）上不同的三点，连接OA、OB、OC，过点A作AD⊥y轴于点D，过点B、C分别作BE，CF垂直x轴于点E、F，OC与BE相交于点M，记△AOD、△BOM、四边形CMEF的面积分别为S₁、S₂、S₃ ，则（）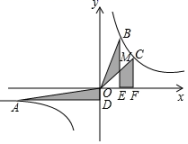

A、S₁=S₂+S₃ B、S₂=S₃ C、S₃＞S₂＞S₁ D、S₁S₂＜S₃²

查看试题解析

二、填空题

7. 函数 $y = \sqrt{2 - x}$ 的定义域为．

查看试题解析
8. 已知函数y＝ $\frac{x}{x - 1}$ ，当x＝ $\sqrt{2}$ 时，y＝．

查看试题解析
9. 已知0是关于 $x$ 的一元二次方程 $(m - 1) x^{2} + 2 x + m^{2} - 1 = 0$ 的一个实数根，则 $m$ = ．

查看试题解析
10. 若 $M (- 1 ， y {}_{1})$ 、 $N (- \frac{1}{2} ， y {}_{2})$ 两点都在函数 $y = \frac{k}{x}$ 的图像上，且 $y_{1}$ < $y_{2}$ ，则k的取值范围是．

查看试题解析
11. 已知正比例函数 $y = k x (k \neq 0)$ 的图象经过第一、三象限，且经过点（k，k+2），则k= ．

查看试题解析
12. 以线段AB为底边的等腰三角形，它的两底角平分线交点的轨迹是．

查看试题解析
13. 如图，在△ABC中，∠C=37°，边BC的垂直平分线分别与AC、BC交于点D、E，AB=CD，那么∠A=°．

查看试题解析
14. 如图，∠AOE＝∠BOE＝15°，EF//OB，EC⊥OB，若EC＝2，则EF＝．

查看试题解析
15. 如图，梯形ABCD中，AD∥BC ， AF⊥BC于F ， M是CD中点，AM的延长线交BC的延长线于E ， AE⊥AB ， ∠B=60°，AF= $2 \sqrt{3}$ ，则梯形的面积是．

查看试题解析
16. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt△ABC中，∠C=90° ，AC=2，若Rt△ABC是“好玩三角形”，则AB= ．

查看试题解析
17. 小华用一张直角三角形纸片玩折纸游戏，如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $A C = 1$ ．第一步，在 $A B$ 边上找一点 $D$ ，将纸片沿 $C D$ 折叠，点 $A$ 落在 $A$ 处，如图2，第二步，将纸片沿 $C A$ 折叠，点 $D$ 落在 $D$ 处，如图3．当点 $D$ 恰好在原直角三角形纸片的边上时，线段 $A D$ 的长为．

查看试题解析
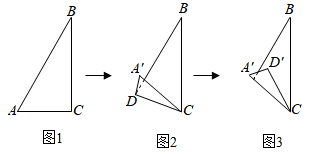18. 在实数范围内因式分解： $2 x^{2} - 3 x - 1 =$ ．

查看试题解析

三、解答题

19. 计算： $\sqrt{2} \times \sqrt{6} + \frac{2}{\sqrt{3} - 1} - {(\sqrt{3} - \sqrt{2})}^{2}$ ．

查看试题解析
20. 用配方法解方程： $x^{2} - 4 x - 2 = 0$ ．

查看试题解析
21. 关于x的一元二次方程 $2 x^{2} + (m - 2) x + 2 = 0$ 有两个相等的实数根，求m的值及方程的根．

查看试题解析
22. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加 $10 %$ ， 5月份的营业额达到633.6万元．求3月份到5月份营业额的平均月增长率．

查看试题解析
23. 接种疫苗是预防控制传染病最有效的手段．甲、乙两地分别对本地各40万人接种新冠病毒疫苗．甲地在前期完成5万人员接种后，甲、乙两地同时以相同速度接种．甲地经过a天接种后，由于情况变化，接种速度放缓．图中的折线BCD和线段OA分别反映了甲、乙两地的接种人数y（万人）与接种时间x（天）之间的函数关系．根据图像所提供的信息回答下列问题

(1)、乙地比甲地提前了天完成疫苗接种工作．

(2)、试写出乙地接种人数 $y_{2}$ （万人）与接种时间x（天）之间的函数解析式．

(3)、当甲地放缓接种速度后，每天可接种万人．

查看试题解析
24. 如图，在△ABC中，∠ACB=90°，AC=4，CB=2，点D是AB的中点，点E在AC上，点E、D、F一条直线上，且ED=FD，

(1)、求证：FB⊥CB；

(2)、联结CD，若CD⊥EF，求CE的长．

查看试题解析
25. 在平面直角坐标系中，反比例函数y＝ $\frac{k}{x}$ （x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．

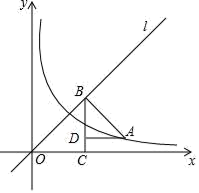(1)、求n的值；

(2)、如图，直线l为正比例函数y＝x的图象，点A在反比例函数y＝ $\frac{k}{x}$ （x＞0，k＞0）的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的面积为S₁ ， △ABD的面积为S₂ ，求S₁﹣S₂的值．

查看试题解析
26. 如图1所示，已知△ABC中，∠ACB=90°，BC=2，AC= $2 \sqrt{3}$ ，点D在射线BC上，以点D为圆心，BD为半径画弧交AB边AB于点E，过点E作EF⊥AB交边AC于点F，射线ED交射线AC于点G．

(1)、求证：EA=EG；

(2)、若点G在线段AC延长线上时，设BD=x，FC=y，求y关于x的函数解析式并写出定义域；

(3)、联结DF，当△DFG是等腰三角形时，请直接写出BD的长度．

查看试题解析