山东省枣庄市峄城区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

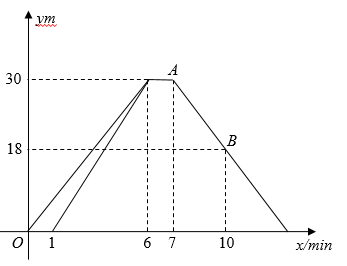
1. 满足下列条件的 $Δ A B C$ ，不是直角三角形的是（）

A、 $b^{2} - c^{2} = a^{2}$ B、 $a : b : c = 5 : 12 : 13$ C、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$ D、 $∠ C = ∠ A - ∠ B$

查看试题解析
2. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃(读 $k u n$ ，门槛的意思)一尺，不合二寸，问门广几何？题目大意是：如图1、2(图2为图1的平面示意图)，推开双门，双门间隙 $C D$ 的距离为 $2$ 寸，点 $C$ 和点 $D$ 距离门槛 $A B$ 都为 $1$ 尺( $1$ 尺 $= 10$ 寸)，则 $A B$ 的长是（）

A、 $50.5$ 寸 B、 $52$ 寸 C、 $101$ 寸 D、 $104$ 寸

查看试题解析
3. 下列无理数，与3最接近的是（）

A、 $\sqrt{6}$ B、 $\sqrt{7}$ C、 $\sqrt{10}$ D、 $\sqrt{11}$

查看试题解析
4. 下列计算正确的是（）

A、 ${(- \sqrt{3})}^{2} = - 3$ B、 $\sqrt{12} = 2 \sqrt{3}$ C、 $\sqrt[3]{-} 1 = 1$ D、 $(\sqrt{2} + 1) (\sqrt{2} - 1) = 3$

查看试题解析
5. 下列说法中：① $(- 1 ， - x^{2})$ 位于第三象限；② $\sqrt{81}$ 的平方根是3；③若 $x + y = 0$ ，则点 $P (x ， y)$ 在第二、四象限角平分线上；④点 $A (2 ， a)$ 和点 $B (b ， - 3)$ 关于 $x$ 轴对称，则 $a + b$ 的值为5；⑤点 $N (1 ， n)$ 到 $x$ 轴的距离为 $n$ ．正确的有（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，若在象棋盘上建立平面直角坐标系xOy，使“帅”的坐标为（﹣1，﹣2）“马”的坐标为（2，﹣2），则“兵”的坐标为（）

A、（﹣3，1） B、（﹣2，1） C、（﹣3，0） D、（﹣2，3）

查看试题解析
7. 甲无人机从地面起飞，乙无人机从距离地面20m高的楼顶起飞，两架无人机同时匀速上升10s．甲、乙两架无人机所在的位置距离地面的高度y（单位：m）与无人机上升的时间x（单位：s）之间的关系如图所示．下列说法正确的是（）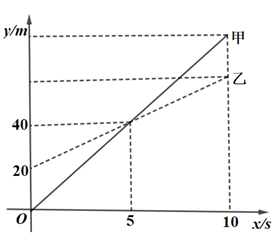

A、5s时，两架无人机都上升了40m B、10s时，两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时，甲无人机距离地面的高度是60m

查看试题解析
8. 已知二元一次方程组 ${\begin{array}{l} 2 x - y = 5 \\ x - 2 y = 1 \end{array}$ ，则 $x - y$ 的值为（）

A、2 B、6 C、 $- 2$ D、 $- 6$

查看试题解析
9. 某中学积极响应党的号召，大力开展各项有益于德智体美劳全面发展的活动小明同学在某学期德智体美劳的评价得分如图所示，则小明同学五项评价的平均得分为（）

A、7分 B、8分 C、9分 D、10分

查看试题解析
10. 《孙子算经》中有一道题，原文是“今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺.问木长多少尺？设木长x尺，绳长y尺，可列方程组为（）

A、 ${\begin{array}{l} x = y + 4.5 \\ \frac{1}{2} x = y + 1 \end{array}$ B、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ C、 ${\begin{array}{l} x = y + 4.5 \\ \frac{1}{2} x = y - 1 \end{array}$ D、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$

查看试题解析
11. 下列命题中的真命题是（）

A、内错角相等，两直线平行 B、相等的角是对顶角 C、 $2^{- 1} = - 2$ D、若 $| a | = 1$ ，则 $a = 1$

查看试题解析
12. 如图，直线 $a / / b$ ，将一个含 $30 °$ 角的三角尺按如图所示的位置放置，若 $∠ 1 ＝ 24 °$ ，则 $∠ 2$ 的度数为（）

A、 $120 °$ B、 $136 °$ C、 $144 °$ D、 $156 °$

查看试题解析

二、填空题

13. 若长方形的周长是 $(30 + 16 \sqrt{5}) c m$ ，一边长是 $(\sqrt{5} - 2) c m$ ，则它的面积是 $c m^{2}$ ．

查看试题解析
14. 如图， $A (6 ， 0)$ ， $C (- 2 ， 0)$ ，以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点B的坐标为．

查看试题解析
15. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16cm，44码鞋子的长度为27cm，则38码鞋子的长度为cm．

查看试题解析
16. 如图，利用函数图象可知方程组 ${\begin{array}{l} x + k y ＝ 3 \\ y ＝ 2 x \end{array}$ 的解为．

查看试题解析
17. 为庆祝中国共产党建党一百周年，某校开展了主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分，最终得分按4：3：3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分，则选手甲的最终得分为分.

查看试题解析
18. 如图，把 $△ A B C$ 纸片沿DE折叠，使点A落在图中的 $A ′$ 处，若 $∠ A = 29 °$ ， $∠ B D A^{'} = 90 °$ ，则 $∠ A^{'} E C$ 的大小为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{45} \times \sqrt{\frac{6}{5}} - \frac{\sqrt{3} + \sqrt{48}}{\sqrt{2}}$ ；

(2)、 $\sqrt{20} - {(2 - \sqrt{5})}^{2} + 10 \sqrt{\frac{1}{5}}$ ．

查看试题解析
20. 解方程组： ${\begin{array}{l} \frac{x + 1}{5} - \frac{y - 1}{2} = - 1 ， \\ x + y = 2 ． \end{array}$

查看试题解析
21. 如图，方格纸中的每个小方格都是边长为1的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，A（﹣5，0）、B（﹣2，4）、C（﹣1，﹣2）．

(1)、画出△ABC关于y轴对称的△A₁B₁C₁；

(2)、直接写出△ABC关于x轴对称的△A₂B₂C₂的三个顶点的坐标；

查看试题解析

22. 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：

	平均数	中位数	众数	方差
甲	175	$a$	$b$	93.75
乙	175	175	180，175，170	$c$

(1)、求

a

、

b

的值；

(2)、若九（1）班选一位成绩稳定的选手参赛，你认为应选谁，请说明理由；

(3)、根据以上的数据分析，请你运用所学统计知识，任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.

查看试题解析

23. 某校为实现垃圾分类投放，准备在校园内摆放大、小两种垃圾桶购买2个大垃圾桶和4个小垃圾桶共需600元；购买6个大垃圾桶和8个小垃圾桶共需1560元．

(1)、求大、小两种垃圾桶的单价；

(2)、该校购买8个大垃圾桶和24个小垃圾桶共需多少元？

查看试题解析
24. 在一次机器“猫”抓机器“鼠”的展演测试中，“鼠”先从起点出发，1min后，“猫”从同一起点出发去追“鼠”，抓住“鼠”并稍作停留后，“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离 $y (m)$ 与时间 $x (\min)$ 之间的关系如图所示.

(1)、在“猫”追“鼠”的过程中，“猫”的平均速度与“鼠”的平均速度的差是 $m / \min$ ；

(2)、求 $A B$ 的函数表达式；

(3)、求“猫”从起点出发到返回至起点所用的时间.

查看试题解析
25. 如图，已知点E在BD上，AE⊥CE且EC平分∠DEF.

(1)、求证：EA平分∠BEF；

(2)、若∠1=∠A，∠4=∠C，求证：AB∥CD.

查看试题解析