辽宁省丹东市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 下列各数: , , 0.6868868886…(相邻两个6之间8的个数逐次加1), , , 其中无理数的个数有( )个.A、1 B、2 C、3 D、42. 在中, , 如果 , , 那么的长是( ).A、10 B、 C、10或 D、73. 在平面直角坐标系中,点在轴上,则点的坐标为( ).A、 B、 C、 D、4. 如图,① , ② , ③ , ④可以判定的条件有( ).
 A、①②④ B、①②③ C、②③④ D、①②③④5. 甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是 , , , , 则这四名同学立定跳远成绩最稳定的是( ).A、甲 B、乙 C、丙 D、丁6. 下列语句是真命题的是( ).A、内错角相等 B、若 , 则 C、直角三角形中,两锐角和的函数关系是一次函数 D、在中, , 那么为直角三角形7. 若一次函数( , 为常数,)的图象不经过第三象限,那么 , 应满足的条件是( )A、且 B、且 C、且 D、且8. 如图所示,一副三角板叠放在一起,则图中等于( )
A、①②④ B、①②③ C、②③④ D、①②③④5. 甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是 , , , , 则这四名同学立定跳远成绩最稳定的是( ).A、甲 B、乙 C、丙 D、丁6. 下列语句是真命题的是( ).A、内错角相等 B、若 , 则 C、直角三角形中,两锐角和的函数关系是一次函数 D、在中, , 那么为直角三角形7. 若一次函数( , 为常数,)的图象不经过第三象限,那么 , 应满足的条件是( )A、且 B、且 C、且 D、且8. 如图所示,一副三角板叠放在一起,则图中等于( ) A、105° B、115° C、120° D、135°9. 如图1,在中, , 点是的中点,动点从点出发沿运动到点 , 设点的运动路程为 , 的面积为 , 与的函数图象如图2所示,则的长为( ).
A、105° B、115° C、120° D、135°9. 如图1,在中, , 点是的中点,动点从点出发沿运动到点 , 设点的运动路程为 , 的面积为 , 与的函数图象如图2所示,则的长为( ).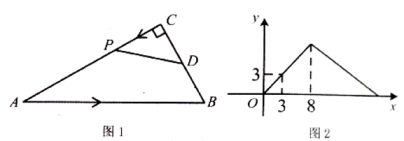 A、10 B、12 C、 D、
A、10 B、12 C、 D、二、填空题
-
10. 的算术平方根是11. 点到轴的距离为 , 到轴的距离为 .12. 有5个数据的平均数为24,另有15个数据的平均数是20,那么所有这20个数据的平均数是 .13. 已知:直线与直线的图象交点如图所示,则方程组的解为 .
 14. 3+的整数部分是a,3- 的小数部分是b,则a+b等于.15. 如图所示,长方体中, , , 是的中点,一只蚂蚁从点出发,沿长方体表面爬到点,则蚂蚁走的最短路径长为 .
14. 3+的整数部分是a,3- 的小数部分是b,则a+b等于.15. 如图所示,长方体中, , , 是的中点,一只蚂蚁从点出发,沿长方体表面爬到点,则蚂蚁走的最短路径长为 . 16. 如图, , 点和点分别在边和边上,连接 , 将沿折叠,点的对应点是 , 若 , 则 .
16. 如图, , 点和点分别在边和边上,连接 , 将沿折叠,点的对应点是 , 若 , 则 .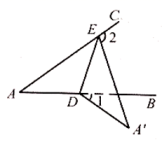 17. 如图,是的角平分线, , , , 则的长为 .
17. 如图,是的角平分线, , , , 则的长为 . 18. 如图1是甲、乙两个圆柱形容器的轴截面示意图,乙容器中有一个圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙容器底面上),现将甲容器中的水匀速注入乙容器,甲、乙两个容器中水的深度与注水时间(分钟)之间的关系如图2所示,若乙容器中铁块的体积是 , 则甲容器的底面积是 .
18. 如图1是甲、乙两个圆柱形容器的轴截面示意图,乙容器中有一个圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙容器底面上),现将甲容器中的水匀速注入乙容器,甲、乙两个容器中水的深度与注水时间(分钟)之间的关系如图2所示,若乙容器中铁块的体积是 , 则甲容器的底面积是 .
三、解答题
-
19. 计算:20. 解方程组:21. 如图,在平面直角坐标系中有 , 两点,坐标分别为 , , 已知点的坐标为
 (1)、确定平面直角坐标系,并画出;(2)、请画出关于轴对称的图形 , 并直接写出的面积;(3)、若轴上存在一点 , 使的值最小.请画图确定点的位置,并直接写出的最小值.22. 如图,已知直线 , , 平分 .
(1)、确定平面直角坐标系,并画出;(2)、请画出关于轴对称的图形 , 并直接写出的面积;(3)、若轴上存在一点 , 使的值最小.请画图确定点的位置,并直接写出的最小值.22. 如图,已知直线 , , 平分 .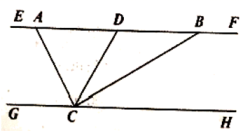 (1)、求证: ;(2)、若 比 的2倍少3度,求 的度数.23. 书籍是人类进行的阶梯.为了解学生的课外阅读情况,某校随机抽查了部分学生本学期阅读课外书的册数,并绘制出如下统计图.
(1)、求证: ;(2)、若 比 的2倍少3度,求 的度数.23. 书籍是人类进行的阶梯.为了解学生的课外阅读情况,某校随机抽查了部分学生本学期阅读课外书的册数,并绘制出如下统计图.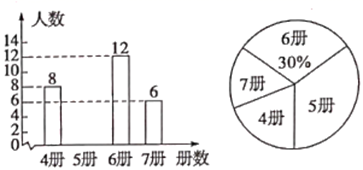 (1)、共抽查了多少名学生?(2)、请补全条形统计图,并写出被抽查学生本学期阅读课外书册数的众数、中位数;(3)、根据抽查结果,请估计该校1200名学生中本学期课外阅读5册书的学生人数.24. 在“新冠疫情”期间,某药店出售普通口罩和N95口罩.下表为两次销售记录:
(1)、共抽查了多少名学生?(2)、请补全条形统计图,并写出被抽查学生本学期阅读课外书册数的众数、中位数;(3)、根据抽查结果,请估计该校1200名学生中本学期课外阅读5册书的学生人数.24. 在“新冠疫情”期间,某药店出售普通口罩和N95口罩.下表为两次销售记录:销售情况
普通口罩/个
N95口罩/个
总销售额/元
第一次
600
100
2400
第二次
400
200
3200
(1)、求每个普通口罩和每个N95口罩的销售价格各是多少元?(2)、该药店计划第三次购进两种口罩共800个,已知普通口罩的进价为1元/个,N95口罩的进价为8元/个,两种口罩的销售单价不变,设此次购进普通口罩个,药店销售完此次购进的两种口罩共获利为元.①求与的函数关系式;
②若销售利润为1400元,则购进两种口罩各多少个?
25. 甲、乙两辆汽车沿同一路线赶赴距出发地300千米的目的地,乙车比甲车晚出发1小时(从甲车出发时开始计时).图中折线、线段分别表示甲、乙两车所行路程(千米)与时间(小时)之间的函数关系对应的图象(线段表示甲出发不足1小时因故停车检修).请根据图象所提供的信息,解决如下问题: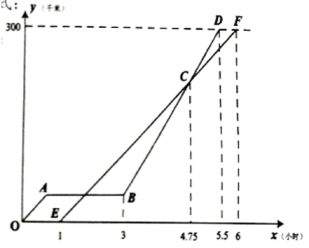 (1)、求乙车行驶的路程与时间的函数关系式;(2)、求甲车发生故障时,距离出发地多少千米;(3)、请直接写出第一次相遇后,经过多长时间两车相距30千米?26. 已知一次函数y=-3x+3的图象分别与x轴,y轴交于A,B两点,点C(3,0).
(1)、求乙车行驶的路程与时间的函数关系式;(2)、求甲车发生故障时,距离出发地多少千米;(3)、请直接写出第一次相遇后,经过多长时间两车相距30千米?26. 已知一次函数y=-3x+3的图象分别与x轴,y轴交于A,B两点,点C(3,0).
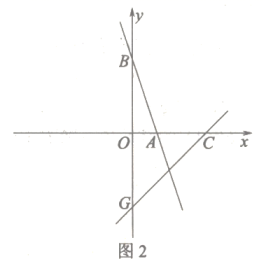 (1)、如图1,点D与点C关于y轴对称,点E在线段BC上且到两坐标轴的距离相等,连接DE,交y轴于点F.求点E的坐标;(2)、△AOB与△FOD是否全等,请说明理由;(3)、如图2,点G与点B关于x轴对称,点P在直线GC上,若△ABP是等腰三角形,直接写出点P的坐标.
(1)、如图1,点D与点C关于y轴对称,点E在线段BC上且到两坐标轴的距离相等,连接DE,交y轴于点F.求点E的坐标;(2)、△AOB与△FOD是否全等,请说明理由;(3)、如图2,点G与点B关于x轴对称,点P在直线GC上,若△ABP是等腰三角形,直接写出点P的坐标.