辽宁省本溪市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根为（）

A、2 B、±2 C、4 D、±4

查看试题解析
2. $△ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别为a，b，c，下列条件能判断 $△ A B C$ 是直角三角形的是（）

A、 $∠ A = ∠ B = ∠ C$ B、 $a = 6$ ， $b = 7$ ， $c = 8$ C、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ D、 $a^{2} + b^{2} = c^{2}$

查看试题解析
3. 在实数3.1415， $\frac{22}{7}$ ， $\sqrt{27}$ ， $\sqrt{4}$ ， 2.8181181118…（相邻两个8之间1的个数逐次加1）中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试，每个人这5次成绩的平均数都是92分，方差分别是 $S_{甲}^{2} = 0.85$ ， $S_{乙}^{2} = 0.72$ ， $S_{丙}^{2} = 0.63$ ， $S_{丁}^{2} = 0.35$ ，则这5次测试成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 下列说法中，错误的是（）

A、对顶角相等 B、三角形内角和等于180° C、三角形的一个外角大于任何一个内角 D、两直线平行，同旁内角互补

查看试题解析
6. 点A的坐标为 $(1 ， 2)$ ，则点A在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，将一个含有30°角的直角三角板放置在两条平行线a，b上，若 $∠ 1 = 115 °$ ，则 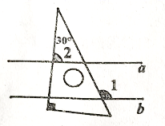$∠ 2$ 的度数为（）

A、85° B、75° C、55° D、95°

查看试题解析
8. 如图，长方形OABC中，点A在y轴上，点C在x轴上． $O A = B C = 4$ ， $A B = O C = 8$ ．点D在边AB上，点E在边OC上，将长方形沿直线DE折叠，使点B与点O重合．则点D的坐标为（）

A、 $(4 ， 4)$ B、 $(5 ， 4)$ C、 $(3 ， 4)$ D、 $(6 ， 4)$

查看试题解析
9. 《孙子算经》记载：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”大致意思是：今有若干人乘车，若每3人共乘一辆车，最终剩余2辆车；若每2人共乘一辆车，最终剩余9人无车可乘．问共有多少人？有多少辆车？若设有x人，有y辆车，根据题意，所列方程组正确的是（）

A、 ${\begin{array}{l} x (x - 2) = y \\ 2 x + 9 = y \end{array}$ B、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y + 9 = x \end{array}$ C、 ${\begin{array}{l} 3 (x - 2) = y \\ 2 y + 9 = x \end{array}$ D、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 x + 9 = y \end{array}$

查看试题解析
10. 如图，在射线AM上顺次取两点B，C，以BC为边作长方形BCDE（长方形的对边平行且相等），若 $A B = B C = 1$ ， $B E = C D = 2$ ，点G在线段CD上（点G不与点C，D重合），作射线 $A G$ 交BE于点F，设 $B F = x$ ， $D G = y$ ，则下列函数图象中，能反映y与x之间大致关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若 $a < \sqrt{11} < b$ ，且a，b是两个连续的整数，则 $a + b$ 的值为．

查看试题解析
12. 若点 $M (a ， 3)$ ， $N (- 4 ， b)$ 关于x轴对称，则b的值为．

查看试题解析
13. 小明某学期数学平时成绩为90分，期中考试成绩为80分，期末成绩为90分，计算学期总评成绩的方法：平时占20%，期中占30%，期末占50%，则小明这学期的总评成绩是分．

查看试题解析
14. 如图，围棋盘的方格内，白棋②的位置是 $(- 5 ， - 2)$ ，白棋④的位置是 $(- 4 ， - 6)$ ，那么黑棋①的位置应该表示为．

查看试题解析
15. 如图，直线l₁：y＝x＋1与直线l₂：y＝mx＋n相交于点P（a，2），则关于x的方程组 ${\begin{cases} \end{cases} \begin{array}{l} y = x + 1 \\ y = m x + n \end{array}$ 的解为．

查看试题解析
16. 若点 $P (m ， n)$ 在直线 $3 x + y = 5$ 上，且m，n都是正整数，则点P坐标是．

查看试题解析
17. 在平面直角坐标系中，点A坐标为 $(4 ， 3)$ ，点B在x轴上，若 $△ A O B$ 是直角三角形，则OB的长为．

查看试题解析
18. 如图， $△ A B C$ 和 $△ D E C$ 都是等边三角形，连接AD，BD，BE， $∠ E B D = 30 °$ ．下列四个结论中：① $△ A C D$ ≌ $△ B C E$ ；② $∠ A D C + ∠ B D E = 180 °$ ；③ $B E^{2} + B D^{2} = B C^{2}$ ；④ $∠ B E D = 90 °$ ，正确的是（填写所有正确结论的序号）．

查看试题解析

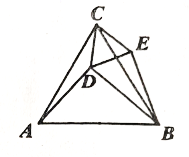
三、解答题

19.

(1)、计算： $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}} + (\sqrt{13} + 3) (\sqrt{13} - 3)$

(2)、解方程组： ${\begin{array}{l} 2 x + 3 y = 16 \\ x + 4 y = 13 \end{array}$

查看试题解析
20. 某中学号召学生开展社会实践活动．学校随机地通过问卷形式调查了200名学生，并将学生参加社会实践活动的天数，绘制了如下不完整的条形统计图：
请根据图中提供的信息，完成下列问题（填入结果和补全图形）：

(1)、补全条形统计图；

(2)、学生参加社会实践活动天数的中位数是天；学生参加社会实践活动天数的众数是天；

(3)、该校共有1500人，请你估计“实践活动时间为5天”的学生有多少人？

查看试题解析
21. 如图所示，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ ，试判断 $∠ A E D$ 与 $∠ C$ 的大小关系，并说明理由．
解：                  ▲                   ．
证明：∵ $∠ 1 + ∠ 2 = 180 °$ （                  ▲                  ）
$∠ 1 = ∠ D F H$ （                  ▲                  ）
∴（                  ▲                  ）
∴ $E H ∥ A B$ （                  ▲                  ）
∴ $∠ 3 = ∠ A D E$ （                  ▲                  ）
∵ $∠ 3 = ∠ B$
∴ $∠ B = ∠ A D E$ （                  ▲                  ）．
∴ $D E ∥ B C$
∴ $∠ A E D = ∠ C$ （                  ▲                  ）

查看试题解析
22. 某商店计划购进篮球和排球共100个进行销售．若购进3个篮球和2个排球需要390元：购进2个篮球和1个排球需要240元．该商店计划篮球每个110元，排球每个75元进行销售．

(1)、求篮球和排球的进货单价；

(2)、若购进篮球m个（ $50 \leq m \leq 65$ ），且篮球和排球全部售出，求该商店获得的最少利润．

查看试题解析
23. 如图，在四边形ABCD中， $A D = B C$ ， $A D ∥ B C$ ，过点A作 $A E ⊥ B C$ 于E，E恰好为BC的中点， $A E = 2 B E$ ．

(1)、直接写出AE与AD之间的数量关系：；位置关系：；

(2)、点P在BE上，作 $E F ⊥ D P$ 于点F，连接AF．求证： $D F - E F = \sqrt{2} A F$ ．

查看试题解析
24. 一辆客车从甲地驶往乙地，同时一辆私家车从乙地驶往甲地（私家车、客车两车速度不变）．图1是私家车离甲地距离为y（千米）与行驶的时间为x（小时）之间的函数图象，图2是两车之间的距离s（千米）与行驶的时间x（小时）之间的函数图象：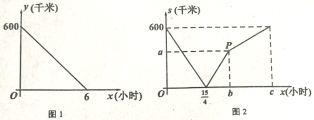

(1)、求私家车和客车的速度各是多少？

(2)、点P的坐标为；c的值为；

(3)、直接写出两车相距200千米时，两车出发的时间x（小时）的值．

查看试题解析
25. 如图，直线AB与x轴交于点 $B (- 3 ， 0)$ ，与y轴交于点C，点A的坐标为 $(1 ， 4)$ ，过点A作 $A D ⊥ x$ 轴，垂足为点D．点E与点B关于y轴对称，直线CE交AD于点F，连接CD．

(1)、求直线AB的解析式：

(2)、点Q为直线AB上一点，当 $△ O B Q$ 与 $△ C D E$ 的面积相等时，求点Q的坐标；

(3)、若点P是坐标平面内一点，请直接写出 $△ C D F$ 与 $△ P A C$ 全等时点P的坐标．

查看试题解析