北京市顺义区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、3 B、 $- 3$ C、 $\pm 3$ D、 $\pm \sqrt{3}$

查看试题解析
2. 若分式 $\frac{x - 1}{x + 1}$ 有意义，则实数 $x$ 的取值范围是（）

A、 $x \neq 1$ B、 $x \neq - 1$ C、 $x = 1$ D、 $x = - 1$

查看试题解析
3. 下列三角形是轴对称图形，且对称轴不只1条的是（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
4. 在下列长度的四根木棒中，能与3cm，9cm的两根木棒首尾顺次相接钉成一个三角形的是（）

A、3cm B、6cm C、10cm D、12cm

查看试题解析
5. 任意掷一枚质地均匀的骰子，偶数点朝上的可能性是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 下列以a，b，c为边的三角形不是直角三角形的是（）

A、a＝1，b＝1，c＝ $\sqrt{2}$ B、a＝2，b＝3，c＝ $\sqrt{13}$ C、a＝3，b＝5，c＝7 D、a＝6，b＝8，c＝10

查看试题解析
7. 如图是一个可以转动的转盘．盘面上有6个全等的扇形区域，其中1个是红色，2个是黄色，3个是白色．用力转动转盘，当转盘停止后，指针对准黄色区域的可能性是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. 当 $m < 0$ 时，化简二次根式 $\frac{m}{n} \sqrt{\frac{n}{m}}$ ，结果正确的是（）

A、 $n \sqrt{m n}$ B、 $- n \sqrt{m n}$ C、 $\frac{1}{n} \sqrt{m n}$ D、 $- \frac{1}{n} \sqrt{m n}$

查看试题解析
9. 乒乓球比赛以11分为1局，水平相当的甲、乙两人进行乒乓球比赛，在一局比赛中，甲已经得了8分，乙只得了2分，对这局比赛的结果进行预判，下列说法正确的是（）

A、甲获胜的可能性比乙大 B、乙获胜的可能性比甲大 C、甲、乙获胜的可能性一样大 D、无法判断

查看试题解析
10. 如图，△ABC中，直线l是边AB的垂直平分线，若直线l上存在点P，使得△PAC，△PAB均为等腰三角形，则满足条件的点P的个数共有（）

A、1 B、3 C、5 D、7

查看试题解析

二、填空题

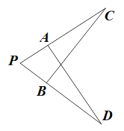
11. 如果分式 $\frac{4 x - 1}{2 x + 3}$ 的值为0，则x的值是．

查看试题解析
12. 最接近 $\sqrt{17}$ 的整数是．

查看试题解析
13. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
14. 如图，PA＝PB，请你添加一个适当的条件：，使得△PAD≌△PBC．

查看试题解析
15. 一个盒子里装有除颜色外都相同的1个红球，4个黄球．把下列事件的序号填入下表的对应栏目中．
①从盒子中随机摸出1个球，摸出的是黄球；
②从盒子中随机摸出1个球，摸出的是白球；
③从盒子中随机摸出2个球，至少有1个是黄球．
事件
必然事件
不可能事件
随机事件
序号

查看试题解析
16. 等腰三角形中，一条边长是2cm，另一条边长是3cm，这个等腰三角形的周长是．

查看试题解析
17. 已知：公式 $\frac{P_{1}}{V_{2}} = \frac{P_{2}}{V_{1}} ，$ 其中 $P_{1}$ ， $P_{2}$ ， $V_{1}$ ， $V_{2}$ 均不为零．则 $P_{2} =$ ．（用含有 $P_{1}$ ， $V_{1}$ ， $V_{2}$ 的式子表示）

查看试题解析
18. 如图，在△ABC中，∠ACB＝90°，点D在AB上，将△ABC沿CD折叠，点A落在BC边上的点 $A$ 处，若∠B＝35°，则 $∠ B D A$ 的度数为．

查看试题解析
19. 某班共有36名同学，其中男生16人，喜欢数学的同学有12人，喜欢体育的同学有24人．从该班同学的学号中随意抽取1名同学，设这名同学是女生的可能性为a，这名同学喜欢数学的可能性为b，这名同学喜欢体育的可能性为c，则a，b，c的大小关系是．

查看试题解析
20. 对于任意的正数 $a$ ， $b$ ，定义运算“*”如下： $a * b = {\begin{array}{l} \sqrt{a} - \sqrt{b} (a \geq b) \\ \sqrt{b} - \sqrt{a} (a < b) \end{array}$ ，计算 $(3 * 2) + (48 * 50)$ 的结果为．

查看试题解析

三、解答题

21. 计算： $\sqrt{3} \times \sqrt{6} \div \sqrt{8}$ ．

查看试题解析
22. 计算： $2 \sqrt{12} - \frac{3}{\sqrt{3}} + \sqrt{27}$ ．

查看试题解析
23. 已知：如图，E，F是线段BC上两点，AB $∥$ CD，BE＝CF，∠A＝∠D．求证：AF＝DE．

查看试题解析
24. 计算： $\frac{x^{2} + 4}{x^{2} - 4} - \frac{x - 3}{x - 2} \div \frac{x - 3}{x}$ ．

查看试题解析
25. 解方程： $\frac{x + 1}{x - 1} - \frac{3}{x + 1} = 1$ ．

查看试题解析
26. 计算： ${(\sqrt{6} - 2 \sqrt{3})}^{2} - \sqrt{2} (\sqrt{8} - \sqrt{\frac{1}{2}})$

查看试题解析
27. 先化简，再求值： $\frac{x}{x + 3} - \frac{1 - 3 x}{x^{2} + 6 x + 9}$ ，其中 $x^{2} + 6 x - 3 = 0$ ．

查看试题解析
28. 已知：如图，Rt△ABC中，∠C＝90°，CA＝CB，D是边CB上一点，DE⊥AB于点E，且CD＝BE．求证：AD平分∠BAC．

查看试题解析
29. “三等分角”是被称为几何三大难题的三个古希腊作图难题之一．如图1所示的“三等分角仪”是利用阿基米德原理做出的．这个仪器由两根有槽的棒PA，PB组成，两根棒在P点相连并可绕点P旋转，C点是棒PA上的一个固定点，点A，O可在棒PA，PB内的槽中滑动，且始终保持OA＝OC＝PC．∠AOB为要三等分的任意角．则利用“三等分角仪”可以得到∠APB ＝ $\frac{1}{3}$ ∠AOB．
我们把“三等分角仪”抽象成如图2所示的图形，完成下面的证明．
已知：如图2，点O，C分别在∠APB的边PB，PA上，且OA＝OC＝PC．
求证：∠APB ＝ $\frac{1}{3}$ ∠AOB．

查看试题解析
30. 列方程解应用题：某市为了缓解交通拥堵现象，决定修建一条轻轨铁路的延长线，为使该延长线工程比原计划提前1个月完成，在保证质量的前提下，必须把工作效率提高10%．问原计划完成这项工程需要用多少个月？

查看试题解析
31. 已知：在△ABC中，AB＝AC，直线l过点A ．

(1)、如图1，∠BAC＝90°，分别过点B，C作直线l的垂线段BD，CE，垂足分别为D，E．
①依题意补全图1；
②用等式表示线段DE，BD，CE之间的数量关系，并证明；

(2)、如图2，当∠BAC≠90°时，设∠BAC＝α（0°＜ α ＜180°），作∠CEA＝∠BDA＝α，点D，E在直线l上，直接用等式表示线段DE，BD，CE之间的数量关系为．

查看试题解析
32. 我们定义：在等腰三角形中，腰与底的比值叫做等腰三角形的正度．如图1，在△ABC中，AB＝AC， $\frac{A B}{B C}$ 的值为△ABC的正度．
已知：在△ABC中，AB＝AC，若D是△ABC边上的动点（D与A，B，C不重合）．

(1)、若∠A＝90°，则△ABC的正度为；

(2)、在图1，当点D在腰AB上（D与A、B不重合）时，请用尺规作出等腰△ACD，保留作图痕迹；若△ACD的正度是 $\frac{\sqrt{2}}{2}$ ，求∠A的度数．

(3)、若∠A是钝角，如图2，△ABC的正度为 $\frac{3}{5}$ ， △ABC的周长为22，是否存在点D，使△ACD具有正度？若存在，求出△ACD的正度；若不存在，说明理由．

查看试题解析

事件	必然事件	不可能事件	随机事件
序号