北京市东城区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 在第32届夏季奥林匹克运动会(即2020年东京奥运会)上,中国健儿勇于挑战,超越自我,生动诠释了奥林匹克精神和中华体育精神,共获得38金32银18铜的骄人战绩.在下列的运动标识中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 肥皂属于碱性,碱性会破坏细菌的内部结构,对去除细菌有很强的效果,用肥皂洗手对预防传染疾病起到很重要的作用.肥皂泡的泡壁厚度大约是0.0000007m,将数字0.0000007用科学记数法表示应为( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 下列分式中是最简分式的是( )A、 B、 C、 D、6. 如图,BD是的角平分线, , 交AB于点E.若 , , 则的度数是( )
2. 肥皂属于碱性,碱性会破坏细菌的内部结构,对去除细菌有很强的效果,用肥皂洗手对预防传染疾病起到很重要的作用.肥皂泡的泡壁厚度大约是0.0000007m,将数字0.0000007用科学记数法表示应为( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 下列分式中是最简分式的是( )A、 B、 C、 D、6. 如图,BD是的角平分线, , 交AB于点E.若 , , 则的度数是( )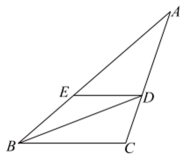 A、10° B、20° C、30° D、50°7. 如图, , AC,BD相交于点O.添加一个条件,不一定能使≌的是( )
A、10° B、20° C、30° D、50°7. 如图, , AC,BD相交于点O.添加一个条件,不一定能使≌的是( ) A、 B、 C、 D、8. 如图,在中,AE的垂直平分线MN交BE于点C,连接AC.若 , , , 则的周长等于( )
A、 B、 C、 D、8. 如图,在中,AE的垂直平分线MN交BE于点C,连接AC.若 , , , 则的周长等于( )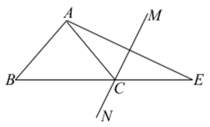 A、11 B、16 C、17 D、189. 若的运算结果中不含项和常数项,则m,n的值分别为( )A、 , B、 , C、 , D、 ,10. 如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下条线段的长度( )
A、11 B、16 C、17 D、189. 若的运算结果中不含项和常数项,则m,n的值分别为( )A、 , B、 , C、 , D、 ,10. 如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下条线段的长度( )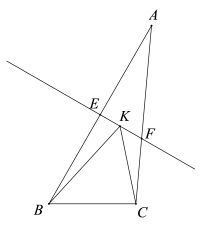 A、EF B、AB C、AC D、BC
A、EF B、AB C、AC D、BC二、填空题
-
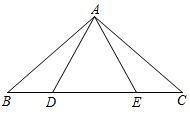
11. 分解因式: .12. 当x时,分式 有意义.13. .14. 若一个正多边形的每一个外角都等于 , 则这个正多边形的边数为 .15. 如图,点 、 、 、 在一条直线上,若 , , ,则 的长为.
 16. 如图,BD,CE是等边三角形ABC的中线,BD,CE交于点F,则°.
16. 如图,BD,CE是等边三角形ABC的中线,BD,CE交于点F,则°.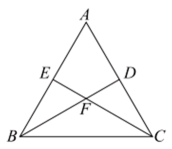 17. 如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释一个等式是 .
17. 如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释一个等式是 .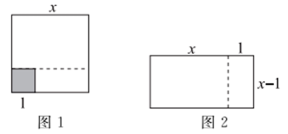 18. 如图,在中, , , , 点C在直线l上.点P从点A出发,在三角形边上沿的路径向终点B运动;点Q从B点出发,在三角形边上沿的路径向终点A运动.点P和Q分别以1单位/秒和2单位/秒的速度同时开始运动,在运动过程中,若有一点先到达终点时,该点停止运动,另一个点要继续运动,直到两点都到达相应的终点时整个运动才能停止.在某时刻,分别过P和Q作于点E,于点F,则点P的运动时间等于秒时,与全等.
18. 如图,在中, , , , 点C在直线l上.点P从点A出发,在三角形边上沿的路径向终点B运动;点Q从B点出发,在三角形边上沿的路径向终点A运动.点P和Q分别以1单位/秒和2单位/秒的速度同时开始运动,在运动过程中,若有一点先到达终点时,该点停止运动,另一个点要继续运动,直到两点都到达相应的终点时整个运动才能停止.在某时刻,分别过P和Q作于点E,于点F,则点P的运动时间等于秒时,与全等.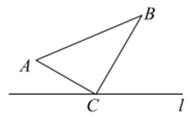
三、解答题
-
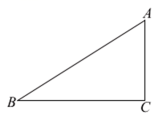
19. 如图,在中, , . 分别以点A,B为圆心,大于的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF为半径画弧,交BC延长线于点H,连接AH.
 (1)、使用直尺和圆规完成作图过程(保留作图痕迹);(2)、通过作图过程,可以发现直线DE是线段AB的 , 是三角形;(3)、若 , 则的周长为 .20. 计算: .21.(1)、已知: , 求代数式的值.(2)、先化简 , 然后选一个合适的x值代入,求出代数式的值.22. 解分式方程: .23. 如图,在平面直角坐标系xOy中,直线l是第一、三象限的角平分线.已知的三个顶点坐标分别为 , , .
(1)、使用直尺和圆规完成作图过程(保留作图痕迹);(2)、通过作图过程,可以发现直线DE是线段AB的 , 是三角形;(3)、若 , 则的周长为 .20. 计算: .21.(1)、已知: , 求代数式的值.(2)、先化简 , 然后选一个合适的x值代入,求出代数式的值.22. 解分式方程: .23. 如图,在平面直角坐标系xOy中,直线l是第一、三象限的角平分线.已知的三个顶点坐标分别为 , , .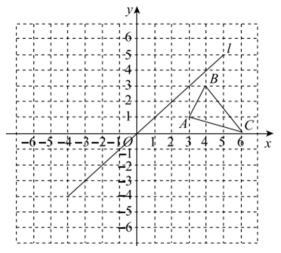 (1)、若与关于y轴对称,画出;(2)、若在直线l上存在点P,使的周长最小,则点P的坐标为 .24. 如图,AD是的高,CE是的角平分线.若 , , 求的度数.
(1)、若与关于y轴对称,画出;(2)、若在直线l上存在点P,使的周长最小,则点P的坐标为 .24. 如图,AD是的高,CE是的角平分线.若 , , 求的度数.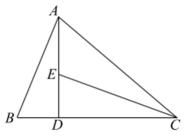 25. 如图,在四边形ABCD中,E是CB上一点,分别延长AE,DC相交于点F, , .
25. 如图,在四边形ABCD中,E是CB上一点,分别延长AE,DC相交于点F, , .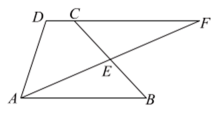 (1)、求证:;(2)、若 , 求BE的长.26. 列方程解应用题:2021年9月23日,我国迎来第四个中国农民丰收节.在庆祝活动中记者了解到:某种粮大户2020年所种粮食总产量约150吨.在强农惠农富农政策的支持下,2021年该农户种粮积极性不断提高,他不仅扩大耕地面积,而且亩产量也大幅提高,因此取得大丰收.已知他2021年比2020年增加20亩耕地,亩产量是2020年的1.2倍,总产量约216吨,那么2020年该农户所种粮食的亩产量约为多少吨?27. 在等腰中, , 点D是BC边上的一个动点(点D不与点B,C重合),连接AD,作等腰 , 使 , , 点D,E在直线AC两旁,连接CE.
(1)、求证:;(2)、若 , 求BE的长.26. 列方程解应用题:2021年9月23日,我国迎来第四个中国农民丰收节.在庆祝活动中记者了解到:某种粮大户2020年所种粮食总产量约150吨.在强农惠农富农政策的支持下,2021年该农户种粮积极性不断提高,他不仅扩大耕地面积,而且亩产量也大幅提高,因此取得大丰收.已知他2021年比2020年增加20亩耕地,亩产量是2020年的1.2倍,总产量约216吨,那么2020年该农户所种粮食的亩产量约为多少吨?27. 在等腰中, , 点D是BC边上的一个动点(点D不与点B,C重合),连接AD,作等腰 , 使 , , 点D,E在直线AC两旁,连接CE.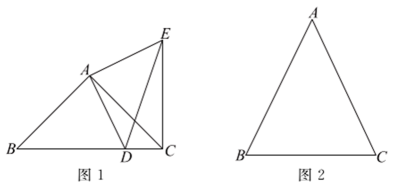 (1)、如图1,当时,直接写出BC与CE的位置关系;(2)、如图2,当时,过点A作于点F,请你在图2中补全图形,用等式表示线段BD,CD,之间的数量关系,并证明.28. 在平面直角坐标系xOy中,将点到x轴和y轴的距离的较大值定义为点M的“相对轴距”,记为 . 即:如果 , 那么;如果 , 那么 . 例如:点的“相对轴距” .
(1)、如图1,当时,直接写出BC与CE的位置关系;(2)、如图2,当时,过点A作于点F,请你在图2中补全图形,用等式表示线段BD,CD,之间的数量关系,并证明.28. 在平面直角坐标系xOy中,将点到x轴和y轴的距离的较大值定义为点M的“相对轴距”,记为 . 即:如果 , 那么;如果 , 那么 . 例如:点的“相对轴距” . (1)、点的“相对轴距”;(2)、请在图1中画出“相对轴距”与点的“相对轴距”相等的点组成的图形;(3)、已知点 , , , 点M,N是内部(含边界)的任意两点.
(1)、点的“相对轴距”;(2)、请在图1中画出“相对轴距”与点的“相对轴距”相等的点组成的图形;(3)、已知点 , , , 点M,N是内部(含边界)的任意两点.①直接写出点M与点N的“相对轴距”之比的取值范围;
②将向左平移个单位得到 , 点与点为内部(含边界)的任意两点,并且点与点的“相对轴距”之比的取值范围和点M与点N的“相对轴距”之比的取值范围相同,请直接写出k的取值范围.