安徽省芜湖市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是（）

A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形

查看试题解析
2. 下列图形中，不是轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）．

A、a²•a³＝a⁶ B、a³÷a＝a³ C、（a²）³＝a⁵ D、（3a²）²＝9a⁴

查看试题解析
4. 多边形的内角和不可能为（）

A、180° B、540° C、1080° D、1200°

查看试题解析
5. 下列因式分解结果正确的是（）

A、 $- x^{2} + 4 x = - x (x + 4)$ B、 $4 x^{2} - y^{2} = (4 x + y) (4 x - y)$ C、 $- x^{2} - 2 x - 1 = - (x + 1)^{2}$ D、 $x^{2} - 5 x - 6 = (x - 2) (x - 3)$

查看试题解析
6. 点P（﹣1，2）关于y轴对称点的坐标是（　　）

A、（1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（2，﹣1）

查看试题解析
7. 某种芯片每个探针单元的面积为 $0.00000164 c m^{2}$ ，0.00000164用科学记数法可表示为（）

A、 $1.64 \times 10^{- 5}$ B、 $1.64 \times 10^{- 6}$ C、 $16.4 \times 10^{- 7}$ D、 $0.164 \times 10^{- 5}$

查看试题解析
8. 对于分式 $\frac{| x | - 2}{x + 2}$ ，下列说法正确的是（）

A、当x＝﹣2时分式有意义 B、当x＝±2时分式的值为零 C、当x＝0时分式无意义 D、当x＝2时分式的值为零

查看试题解析
9. 某灾区恢复生产，计划在一定时间内种60亩蔬菜，实际播种时每天比原计划多种3亩，因此提前一天完成任务，问实际种了几天？现设实际种了 $x$ 天，则可列出方程（）

A、 $\frac{60}{x} - \frac{60}{x + 1} = 3$ B、 $\frac{60}{x - 1} - \frac{60}{x} = 3$ C、 $\frac{60}{x} - \frac{60}{x + 3} = 1$ D、 $\frac{60}{x - 3} - \frac{60}{x} = 1$

查看试题解析
10. 如图，在Rt△ABC中， ∠BCA＝90°，∠A＝30°，CD⊥AB，垂足为点D，则AD与BD之比为（）

A、2∶1 B、3∶1 C、4∶1 D、5∶1

查看试题解析
11. 如图，AC＝BC，∠C＝α，DE⊥AC于E，FD⊥AB于D，则∠EDF等于（）．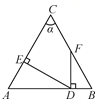

A、α B、90°－ $\frac{1}{2}$ α C、90°－α D、180°－2α

查看试题解析
12. 当x分别取2020、2018、2016、…、4、2、0、 $\frac{1}{2}$ 、 $\frac{1}{4}$ 、…、 $\frac{1}{2016}$ 、 $\frac{1}{2018}$ 、 $\frac{1}{2020}$ 时，计算分式 $\frac{x - 1}{x + 1}$ 的值，再将所得的结果全部相加，则其和等于（）．

A、-1 B、1 C、0 D、2020

查看试题解析

二、填空题

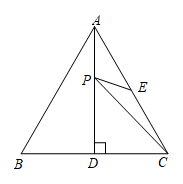
13. 一个等腰三角形的一边长为2，另一边长为9，则它的周长是．

查看试题解析
14. 已知a+b＝4，ab＝1，则a³b+2a²b²+ab³的值为．

查看试题解析
15. 已知关于x的方程 $\frac{2 x + m}{x - 2}$ ＝3的解是正数，则m的取值范围为．

查看试题解析
16. 如图， $△ A B C$ 是等边三角形， $A D$ 是 $B C$ 边上的高， $E$ 是 $A C$ 的中点， $P$ 是 $A D$ 上的一个动点，当 $P C$ 与 $P E$ 的和最小时， $∠ A C P =$ 度．

查看试题解析
17. 如图，线段AB、BC的垂直平分线l₁、l₂相交于点O，若∠1＝37°，则∠AOC＝．

查看试题解析
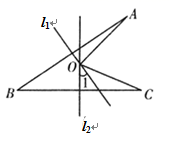18. 观察下列方程：①x+ $\frac{2}{x}$ =3；②x+ $\frac{6}{x}$ =5；③x+ $\frac{12}{x}$ =7，可以发现它们的解分别是①x=1或2；②x=2或3；③x=3或4．利用上述材料所反映出来的规律，可知关于x的方程x+ $\frac{n^{2} + n}{x - 3}$ =2n+4（n为正整数）的解x= ．

查看试题解析

三、解答题

19. 如图，△ABC的顶点A、B、C都在小正方形的顶点上，利用网格线按下列要求画图．
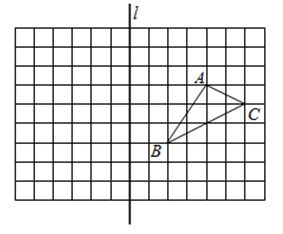
（ 1 ）画△A₁B₁C₁ ，使它与△ABC关于直线l成轴对称；
（ 2 ）在直线l上找一点P，使点P到点A、B的距离之和最短；
（ 3 ）在直线l上找一点Q，使点Q到边AC、BC所在直线的距离相等．

查看试题解析
20. 有一道题：“先化简，再求值： $(\frac{x - 2}{x + 2} + \frac{4 x}{x^{2} - 4})$ ÷ $\frac{1}{x^{2} - 4}$ ，其中x= -6．”小张做题时把x= -6错抄成x=6，但是他的计算结果却是正确的．请你阐明原因．

查看试题解析
21. 为积极创建全国文明城市，甲、乙两工程队承包了我市某街道路面改造工程．若由甲、乙两工程队合做20天可以完成；若甲工程队先单独施工40天，再由乙工程队单独施工10天也可以完成．求甲、乙两工程队单独完成此项工程各需要多少天？

查看试题解析
22. 观察下列等式：
第1个等式：1²＝1³；
第2个等式：（1+2）²＝1³+2³；
第3个等式：（1+2+3）²＝1³+2³+3³；
第4个等式：（1+2+3+4）²＝1³+2³+3³+4³；
……
按照以上规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出第n（n为正整数）个等式：（用含n的等式表示）；

(3)、利用上述规律求值： $\frac{1 1^{3} + 1 2^{3} + 1 3^{3} + ⋯ + 2 0^{3}}{11 + 12 + 13 + ⋯ + 20}$ ．

查看试题解析
23. 如图1，在△ABC中，BE、CF分别平分∠ABC和∠ACB，BE和CF相交于D点．

(1)、求证：∠BDC=90°+ $\frac{1}{2} ∠ A$ ；

(2)、如图2，若∠A＝∠ABE，求证：EB+EC＝BC+BF．

查看试题解析