安徽省合肥市包河区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-13 类型:期末考试
一、单选题
-
1. 下列曲线中表示y是x的函数的是( )A、
 B、
B、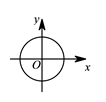 C、
C、 D、
D、 2. 在平面直角坐标系中,点P(-2,1)向右平移3个单位后位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各组数中,不能作为一个三角形三边长的是( )A、4,4,4 B、2,7,9 C、3,4,5 D、5,7,94. 关于一次函数 ,下列说法错误的是( )A、图象经过点(2,0) B、图象经过第三象限 C、函数y随自变量x的增大而减小 D、当x≥2时,y≤05. 已知△ABC的内角分别为∠A、∠B、∠C,下列能判定△ABC是直角三角形的条件是( )A、∠A=2∠B=3∠C B、∠C=2∠B C、∠A+∠B=∠C D、∠A:∠B:∠C= =3:4:56. 下列命题中,逆命题是真命题的是( )A、对顶角相等 B、全等三角形的对应角相等 C、若 ,则 . D、若 ,则7. 在同一直角坐标系中,一次函数y=kx+k与正比例函数y=kx的图像可能是( )A、
2. 在平面直角坐标系中,点P(-2,1)向右平移3个单位后位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各组数中,不能作为一个三角形三边长的是( )A、4,4,4 B、2,7,9 C、3,4,5 D、5,7,94. 关于一次函数 ,下列说法错误的是( )A、图象经过点(2,0) B、图象经过第三象限 C、函数y随自变量x的增大而减小 D、当x≥2时,y≤05. 已知△ABC的内角分别为∠A、∠B、∠C,下列能判定△ABC是直角三角形的条件是( )A、∠A=2∠B=3∠C B、∠C=2∠B C、∠A+∠B=∠C D、∠A:∠B:∠C= =3:4:56. 下列命题中,逆命题是真命题的是( )A、对顶角相等 B、全等三角形的对应角相等 C、若 ,则 . D、若 ,则7. 在同一直角坐标系中,一次函数y=kx+k与正比例函数y=kx的图像可能是( )A、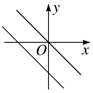 B、
B、 C、
C、 D、
D、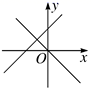 8. 如图,已知AC=DB,添加下列条件,仍不能判断△ABC≌△DCB的是( )
8. 如图,已知AC=DB,添加下列条件,仍不能判断△ABC≌△DCB的是( )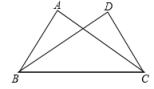 A、∠A=∠D=90° B、∠ABC=∠DCB C、∠ACB=∠DBC D、AB=DC9. 若直线y=2x-1与y=x-k的交点在第四象限,则k的取值范围是( )A、 B、 C、 或 D、10. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息、已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相聚180米有2个时刻,分别是t=18和t=24.其中正确的结论有( )
A、∠A=∠D=90° B、∠ABC=∠DCB C、∠ACB=∠DBC D、AB=DC9. 若直线y=2x-1与y=x-k的交点在第四象限,则k的取值范围是( )A、 B、 C、 或 D、10. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息、已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相聚180米有2个时刻,分别是t=18和t=24.其中正确的结论有( ) A、①② B、①③ C、②④ D、①②④
A、①② B、①③ C、②④ D、①②④二、填空题
-
11. 在函数y= 中,自变量x的取值范围是 .12. 若点P(-1,7)在一次函数y=(3k+2)x-1的图象上,则k的值为 .13. 已知,在△ABC中,∠B=48°,∠C=68°,AD是BC边上的高,AE平分∠BAC,则∠DAE的度数为 .14. 如图,在ΔABC中,∠ACB=90°,点D在AB上,将ΔBDC沿CD折叠,点B落在AC边上的点B′处,若∠ADB′=20°,则∠A的度数是.
 15. 已知直线y=x+b和y=ax+2交于点P(3,-1),则关于x的方程(a-1)x=b-2的解为 .16. 如图,∠AOB=120°,点P为∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON=OP;③四边形PMON的面积保持不变;④△PMN的周长保持不变.其中说法正确的是 . (填序号)
15. 已知直线y=x+b和y=ax+2交于点P(3,-1),则关于x的方程(a-1)x=b-2的解为 .16. 如图,∠AOB=120°,点P为∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON=OP;③四边形PMON的面积保持不变;④△PMN的周长保持不变.其中说法正确的是 . (填序号) 17. 不等边△ABC的两条高的长度分别为4和12,若第三条高也为整数,那么它的长度最大值是
17. 不等边△ABC的两条高的长度分别为4和12,若第三条高也为整数,那么它的长度最大值是三、解答题
-
18. 已知y与x+3成正比例,且x=3时,y=12.(1)、求y与x之间的函数表达式;(2)、当x=-2时,求对应的函数值y.19. 如图,已知△ABC的三个顶点分别为A(-2,4)、B(-6,0)、C(-1,0).
 (1)、将△ABC沿y轴翻折,画出翻折后图形△A1B1C1 , 并写出点A1的坐标;(2)、在y轴上确定一点P,使AP+PB的值最小,直接写出点P的坐标;(3)、若△DBC与△ABC全等,请找出符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.20. 如图,在△ABC中,∠B=∠C , 点D、E、F分别在AB、BC、AC边上,且BE=CF , AD+EC=AB .
(1)、将△ABC沿y轴翻折,画出翻折后图形△A1B1C1 , 并写出点A1的坐标;(2)、在y轴上确定一点P,使AP+PB的值最小,直接写出点P的坐标;(3)、若△DBC与△ABC全等,请找出符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.20. 如图,在△ABC中,∠B=∠C , 点D、E、F分别在AB、BC、AC边上,且BE=CF , AD+EC=AB . (1)、求证:DE=EF;(2)、当∠A=36°时,求∠DEF的度数.21. 如图,直线y=kx+3与x轴、y轴分别相交于点E、F,点E的坐标为(4,0),点A的坐标为(3,0),点P(x,y)是直线上的一个动点(点P不与点E重合).
(1)、求证:DE=EF;(2)、当∠A=36°时,求∠DEF的度数.21. 如图,直线y=kx+3与x轴、y轴分别相交于点E、F,点E的坐标为(4,0),点A的坐标为(3,0),点P(x,y)是直线上的一个动点(点P不与点E重合). (1)、求k的值;(2)、若△OPA的面积为3,求此时点P的坐标.22. 在等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接FC.
(1)、求k的值;(2)、若△OPA的面积为3,求此时点P的坐标.22. 在等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接FC. (1)、如图1,求证:∠ABE=∠ACF;(2)、如图2,当∠ABC=60°时,在BE上取点M,使BM=EF,连接AM.求证:△AFM是等边三角形;(3)、如图3,当∠ABC=45°,且AEBC时,求证:BD=2EF.
(1)、如图1,求证:∠ABE=∠ACF;(2)、如图2,当∠ABC=60°时,在BE上取点M,使BM=EF,连接AM.求证:△AFM是等边三角形;(3)、如图3,当∠ABC=45°,且AEBC时,求证:BD=2EF.