苏科版初中数学七年级下册 7.2 探索平行线的性质（基础版）

试卷更新日期：2022-02-12 类型：同步测试

进入出卷网下载

一、单选题

1. 如图所示，直线a∥b．AC⊥AB．AC交直线b于点C．∠1=65°．则∠2的度数是（）

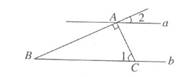A、65° B、50° C、35° D、25°

查看试题解析
2. 如图，直线AB//CD，直线EF分别与直线AB，CD相交于点G，H.若 $∠$ 1=135°，则 $∠$ 2的度数为（）

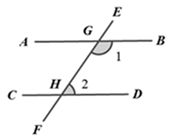A、65° B、55° C、45° D、35°

查看试题解析
3. 如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝40°，则∠2等于（）

A、130° B、140° C、150° D、160°

查看试题解析
4. 如图，∠BAC＝35°，∠CBD＝65°，AE∥BC，则∠CAE的度数为（）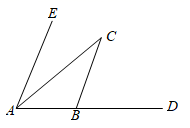

A、50° B、40° C、30° D、20°

查看试题解析
5. 如图，AF//BG，AC//EG，那么图中与∠A相等的角有 $（$ $）$ 个.

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，已知 $A B / / C D$ ，则下列结论中正确的是（）

A、 $∠ E A D = ∠ A B C$ B、 $∠ B A C = ∠ D C A$ C、 $∠ A D B = ∠ D B C$ D、 $∠ A D C + ∠ B C D = 180 °$

查看试题解析
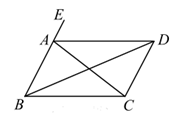7. 如图，已知CB∥DF，则下列结论成立的是（）

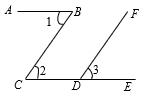A、∠1＝∠2 B、∠2＝∠3 C、∠1＝∠3 D、∠1＋∠2＝180º

查看试题解析
8. 如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么∠1+∠2+∠3=（）.

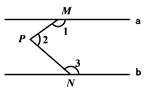A、180° B、360° C、270° D、540°

查看试题解析
9. 如图，如果AB∥EF，EF∥CD，下列各式正确的是（）

A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°

查看试题解析
10. 如图，AB∥CD，∠EAF=3∠BAF，∠ECF=3∠DCF，则∠E与∠F的数量关系是（）

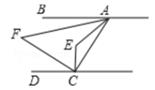A、∠E+∠F=180° B、∠E=3∠F C、∠E-∠F=90° D、∠E=4∠F

查看试题解析

二、填空题

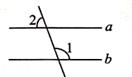
11. 如图，已知a∥b，∠1=110°，则∠2的度数是

查看试题解析
12. 如图，∠1＝∠2，∠D＝75°，则∠BCD＝.

查看试题解析
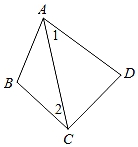13. 如图，AB∥CD，CE∥GF，若∠1＝60°，则∠2＝°.

查看试题解析
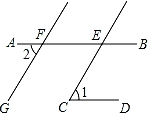14. 如图，将三角板的直角顶点落在直尺的一边上，若 $∠ 1 = 34 °$ ，则 $∠ 2$ 的度数为.

查看试题解析
15. 如图，已知∠1＝∠2＝75°，∠3＝50°，则∠B的大小为 .

查看试题解析
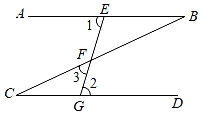16. 如图，在△ABC中，已知DE//BC ， ∠1=∠2，∠BEC=96°，则∠FGE=°

查看试题解析
17. 如图，已知AB//CD//EF，则∠1＝60°，∠3＝20°，则∠2＝.

查看试题解析
18. 如图，已知 $A B$ // $C D$ ，直线 $E F$ 与 $A B$ 、 $C D$ 分别相交于点E、F ， $E P ⊥ E F$ ， $∠ E F D$ 的平分线与 $E P$ 相交于点P ，且 $∠ B E P = 30 °$ ，那么 $∠ E F P$ 的度数为．

查看试题解析

三、解答题

19. 如图，AB∥CD，CB∥DE，若∠B＝70°，求∠D的度数.

查看试题解析
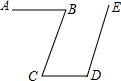20. 如图，已知直线AB∥DF，∠D+∠B=180°，如果∠AMD=75°，求∠AGC的度数．

查看试题解析
21. 如图，已知DE∥BC ， CD是∠ACB的平分线，∠B＝70°，∠ACB＝50°，求∠EDC和∠AED的度数．

查看试题解析
22. 如图，已知 $A B ∥ C D$ ， $∠ B = 60 °$ ， $∠ F C G = 90 °$ ， $C F$ 平分 $∠ B C E$ ，求 $∠ B C G$ 的度数．

查看试题解析
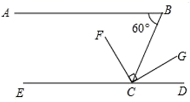23. 如图，EF⊥BC于点F ， ∠1＝∠2，DG∥BA ，若∠2＝40°，则∠BDG是多少度？

查看试题解析
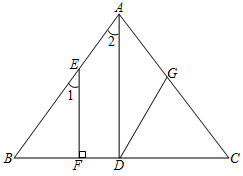24. 根据下列证明过程填空：已知：如图， $A D ⊥ B C$ 于点 $D$ ， $E F ⊥ B C$ 于点 $F$ ， $∠ 4 = ∠ C$ .求证： $∠ 1 = ∠ 2$ .

证明：∵ $A D ⊥ B C$ ， $E F ⊥ B C$ （已知）

∴ $∠ A D C =______= 90 °$ （            ）

∴ $A D / / E F$ （            ）

∴ $∠ 1 =______$ （            ）

又∵ $∠ 4 = ∠ C$ （已知）

∴ $A C / /______$ （            ）

∴ $∠ 2 =______$ （            ）

∴ $∠ 1 = ∠ 2$ （            ）

查看试题解析
25. 如图1，已知：AB∥CD，点E、F分别在AB、CD上，且OE⊥OF．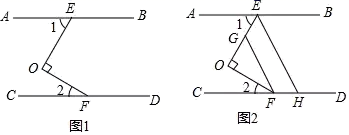

(1)、求∠1＋∠2的度数；

(2)、如图2，分别在OE、CD上取点G、H，使FO平分∠CFG，OE平分∠AEH，试说明FG∥EH．

查看试题解析
26. 已知一个角的两边与另一个角的两边分别平行，请结合图形，探索这两个角之间的数量关系．

(1)、如图1，AB∥CD，BE∥DF，探索∠1与∠2的数量关系，并说明理由；

(2)、如图2，AB∥CD，BE∥DF．探索∠1与∠2的数量关系，并说明理由；

(3)、若∠ABE=80°，且AB∥CD，BE∥DF．直接写出∠CDF的度数．

查看试题解析
27. 如图，已知 $A M / / B N$ ， $∠ A = 60 °$ ，点P是射线AM上一动点（与点A不重合），BC，BD分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线AM于点C，D．

(1)、求 $∠ C B D$ 的度数

(2)、当点P运动时， $∠ A P B ： ∠ A D B$ 的比值是否随之变化？若不变，请求出这个比值；若变化，请找出变化规律；

(3)、当点P运动到某处时， $∠ A C B = ∠ A B D$ ，求此时 $∠ A B C$ 的度数．

查看试题解析
28. 丁丁学习七年级下册数学后，遇到了一些问题，请你帮他解决一下．

(1)、如图1，已知AB $/ /$ CD ，点E在两平行线的内侧，连接AE ， CE ．若∠EAB＝35°，∠ECD＝25°，求∠AEC的度数；（提示：过点E作AB的平行线）

(2)、如图2，已知AB $/ /$ CD ，点E在两平行线的外侧，连接AE ， CE ．若∠EAB＝α ， ∠ECD＝β ．
①求∠AEC的大小（用含α ， β的代数式表示）；

②作∠ECD的平分线交AB于点G ，连接GE ， AG平分于∠CGE（如图3）．若∠AEG＝130°，α+β＝80°，分别求出α ， β的度数．

查看试题解析