2022年苏科版初中数学《中考一轮复习》专题五 图形的变换 5.7 解直角三角形
试卷更新日期：2022-02-12 类型：一轮复习
一、单选题
-
1. 某人沿着坡度为1∶的山坡前进了1000 m，则这个人所在的位置升高了（ ）A、1000 m B、500 m C、500m D、m2. 已知Rt△ABC中，∠C＝90°，∠A＝50°，AB＝2，则AC＝（ ）
A、2sin50° B、2sin40° C、2tan50° D、2tan40°3. 如图，某停车场入口的栏杆 ， 从水平位置绕点O旋转到的位置，已知的长为5米．若栏杆的旋转角 ， 则栏杆A端升高的高度为（ ）
A、米 B、米 C、米 D、米4. 如图，小慧的眼睛离地面的距离为 ， 她用三角尺测量广场上的旗杆高度，仰角恰与三角板角的边重合，量得小慧与旗杆之间的距离为 ， 则旗杆的高度（单位：m）为（ ）
A、6.6 B、11.6 C、 D、5. 如图，一艘轮船从位于灯塔C的北偏东60°方向，距离灯塔60海里的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东45°方向上的B处，这时轮船B与小岛A的距离是（ ）
A、30海里 B、60海里 C、120海里 D、（30＋30）海里6. 如图，学校旁边一处斜坡OA上有一棵风景树，树高BC为6.5米，903班数学活动小组在某个时刻测得树的影长CD为2.5米，此时阳光恰好垂直照射在斜坡上，则这个斜坡的坡度为（ ）
A、1：2.6 B、1：2.4 C、12：13 D、13：127. 如图，从点 看一山坡上的电线杆 ，观测点 的仰角是 ，向前走 到达 点，测得顶端点 和杆底端点 的仰角分别是 和 ，则该电线杆 的高度为（ ）m．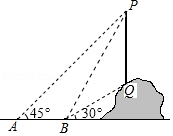
A、 B、 C、 D、8. 如图，一河坝的横断面为等腰梯形ABCD，坝顶宽10米，坝高12米，斜坡AB的坡度i＝1∶1.5，则坝底AD的长度为（ ）
A、26米 B、28米 C、30米 D、46米9. 除了圆以外，最简单的定宽曲线叫做莱洛三角形．即以一个等边三角形的3个顶点为圆心，边长为半径，作各内角所对应的圆弧，擦去原来的等边三角形，剩下的图形就是莱洛三角形，也叫曲边三角形或弧三角形，莱洛三角形是根据十九世纪德国工程师Franz Reuleaux的名字命名的．已知一个莱洛三角形的周长是 ， 则这个莱洛三角形的面积为（ ）A、 B、 C、 D、10. 我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出，“周三径一”不是圆周率值，实际上是圆内接正六边形周长和直径的比值（图1）.刘徽发现，圆内接正多边形边数无限增加时，多边形的周长就无限逼近圆周长，从而创立“割圆术”，为计算圆周率建立起相当严密的理论和完善的算法.如图2，六边形ABCDEF是圆内接正六边形，把每段弧二等分，作出一个圆内接正十二边形，连结AG，CF，AG交CF于点P，AP=2 ， 则 =（ ）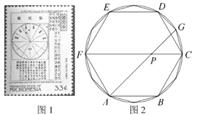
A、2 B、 C、 D、二、填空题
-
11. 如图，在中，是边上的高， ， ， ， 则的长为 ．
12. 如图，物理实验室有一单摆在左右摆动，摆动过程中选取了两个瞬时状态，从C处测的E ， F两点的俯角分别为60°和30°，这时点F相对于点E升高了3cm ． 该摆绳CD的长度为cm ．
13. 如图，在A点有一个热气球，由于受西风的影响，以20米/分的速度沿与地面成角的方向飞行，10分钟后到达C处，此时热气球上的人测得地面上的B点俯角为 ， 则A、B两点间的距离为米．
14. 如图，在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B，C之间的距离为海里．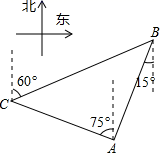
15. 如图，校园内有一棵与地面垂直的树，数学兴趣小组两次测量它在地面上的影子，第一次是阳光与地面成60°角时，第二次是阳光与地面成30角时，已知两次测量的影长相差8米，则树高AB为多少？ ． （结果保留根号）
16. 如图，小石同学在A，B两点分别测得某建筑物上条幅两端C，D两点的仰角均为60°，若点O，A，B在同一直线上，A，B两点间距离为3米，则条幅的高CD为米．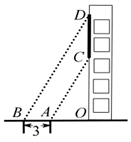
17. 如图，直立于地面上的电线杆 ，在阳光下落在水平地面和坡面上的影子分别是 、 ，测得 米， 米， ，在 处测得电线杆顶端 的仰角为 ，则电线杆 的高度约为米.（参考数据： ， ，结果按四舍五入保留一位小数）
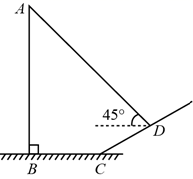18. 勾股定理有着悠久的历史，它曾引起很多人的兴趣．l955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在右图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB=4．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边_PQ上，那么△PQR的周长等于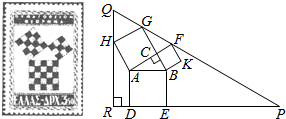
三、解答题
-
19. 热气球的探测器显示，从热气球看一栋高楼顶部的仰角为 ， 看这栋高楼底部的俯角为 ， 热气球与高楼的水平距离为66m，这栋高楼有多高？（结果精确到0.1m，参考数据：）
20. 深圳市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动，如图，此时无人机在离地面30米的点D处，操控者站在点A处，无人机测得点A的俯角为30°，测得教学楼楼顶点C处的俯角为45°，又经过人工测量得到操控者和教学楼BC的距离为57米，求教学楼BC的高度.（ ≈1.7）
21. 如图，从楼层底部 处测得旗杆 的顶端 处的仰角是 ，从楼层顶部 处测得旗杆 的顶端 处的仰角是 ，已知楼层 的楼高为 米.求旗杆 的高度约为多少米?（参考数据： ）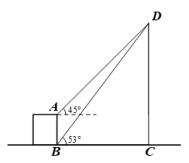
22. 某校为检测师生体温，在校门安装了某型号测温门.如图为该测温门截面示意图，已知测温门AD的顶部A处距地面高为2.2m，为了解自己的有效测温区间.身高1.6m的小聪做了如下实验：当他在地面N处时测温门开始显示额头温度，此时在额头B处测得A的仰角为30°；在地面M处时，测温门停止显示额头温度，此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.（额头到地面的距离以身高计，计算精确到0.1m，≈1.73，≈1.41）
23. 花园小区有一朝向为正南方向的居民楼（如图），该居民楼的一楼是高4米的小区商场，商场以上是居民住房．在该楼的前面16米处要盖一栋高18米的办公楼．当冬季正午的阳光与水平线的夹角为时，问：
(1)、商场以上的居民住房采光是否有影响，为什么？(2)、若要使商场采光不受影响，两楼应相距多少 米？（结果保留一位小数）（参考数据： ， ， ）
24. 如图，在南北方向的海岸线MN上，有A、B两艘巡逻船，现均收到故障船C的求救信号．已知A、B两船相距海里，船C在船A的北偏东60°方向上，船C在船B的东南方向上，MN上有一观测点D，测得船C正好在观测点D的南偏东75°方向上．
(1)、分别求出A与C，A与D之间的距离AC和AD（如果运算结果有根号，请保留根号）．(2)、已知距观测点D处100海里范围内有暗礁．若巡逻船A沿直线AC去营救船C，在去营救的途中有无触暗礁危险﹖请说明理由．（参考数据： ， ， 精确到1海里）25. 淮北市为缓解“停车难”问题．建造地下停车库，如图已知 ， ， C在BD上， ． 根据规定，停车库坡道入口上方要张贴限高标准值，以告知驾驶员能否安全驶入．小明认为CD的长就是限高值，而小亮认为应该以CE的长作为限高值．（参考数据： ， ， ， 结果精确到）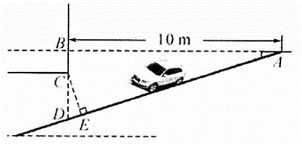
(1)、请你判断小明和小亮谁说的对？(2)、计算出正确的限高值．26. 如图，在建筑物 的左边有一个小山坡，坡底B、C同建筑底端F在同一水平线上，斜坡 的坡比为 ，小李从斜坡底端B沿斜坡走了26米到达坡顶A处，在坡顶A处看建筑物的顶端D的仰角a为35°，然后小李沿斜坡 走了 米到达底部C点，已知建筑物上有一点E，在C处看建筑物E点的仰角 为18°，（点A、B、C、D、E、F在同一平面内）建筑物顶端D到E的距离 长度为28.8米，（参考数据： ， ， ， ）
(1)、求小李从斜坡B走到A处高度上升了多少米.(2)、求建筑物 的高度.27. 如图①是某中型挖掘机，该挖掘机是由基座、主臂和伸展臂构成，图②是共侧面结构示意图（MN是基座，AB是主臂，BC是伸展臂），若主臂AB长为4米，主臂伸展角∠MAB的范围是：30°≤∠MAB≤60°，伸展臂伸展角∠ABC的范围是：45°≤∠ABC≤105°．
(1)、如图③，当∠MAB＝45°，伸展臂BC恰好垂直并接触地面时，求伸展臂BC的长（结果保留根号）；(2)、若（1）中BC长度不变，求该挖掘机最远能挖掘到距A水平正前方多少米的土石．（结果保留根号）28. 如图，斜坡 的坡角 ，计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ，过其另一端 安装支架 ， 所在的直线垂直于水平线 ，垂足为点 为 与 的交点.已知 ，前排光伏板的坡角 .参考数据：
三角函数锐角
13°
28°
32°
0.22
0.47
0.53
0.97
0.88
0.85
0.23
0.53
0.62
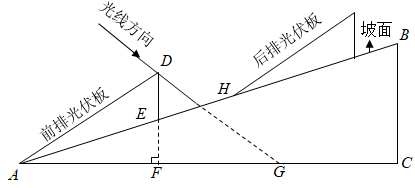(1)、求 的长（结果取整数）；(2)、冬至日正午，经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时，若要后排光伏板的采光不受前排光伏板的影响，则 的最小值为多少（结果取整数）？