2022年苏科版初中数学《中考一轮复习》专题五图形的变换 5.6 锐角三角函数

试卷更新日期：2022-02-12 类型：一轮复习

进入出卷网下载

一、单选题

1. 在Rt $△ A B C$ 中， $∠ C = 9 0^{°} ， A C = 5 ， A B = 13$ ，则 $s i n B$ 的值为（）

A、 $\frac{13}{5}$ B、 $\frac{12}{13}$ C、 $\frac{5}{12}$ D、 $\frac{5}{13}$

查看试题解析
2. 在Rt△ABC中，∠C＝90°，sinA $= \frac{1}{2}$ ，则cosB等于（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
3. 点 $(- s i n 60 ° ， c o s 30 °)$ 关于y轴对称的点的坐标是（）

A、 $(- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ B、 $(\frac{1}{2} ， \frac{\sqrt{3}}{2})$ C、 $(\frac{\sqrt{3}}{2} ， \frac{\sqrt{3}}{2})$ D、 $(- \frac{\sqrt{3}}{2} ， \frac{\sqrt{3}}{2})$

查看试题解析
4. 如图，在 $4 \times 4$ 的正方形网格中，每个小正方形的边长均为1，已知 $∠ α$ 的顶点位于正方形网格的格点上，且 $c o s α = \frac{3 \sqrt{13}}{13}$ ，则满足条件的 $∠ α$ 是（）

A、 B、 C、 D、

查看试题解析
5. 如图，正方形ABCD的边长为1，延长BA至E，使AE＝1，连接EC、ED，则sin∠CED＝（　　）

A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{\sqrt{10}}{10}$ C、 $\frac{\sqrt{5}}{10}$ D、 $\frac{\sqrt{5}}{15}$

查看试题解析
6. 如图，四边形ABCD是菱形，AC＝8，tan∠DAC＝ $\frac{3}{4}$ ，DH⊥AB于H，则点D到AB边距离等于（）

A、4 B、5 C、 $\frac{24}{5}$ D、 $\frac{12}{5}$

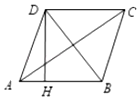查看试题解析
7. 如图，在Rt△ABC中，∠BAC＝90°，过A作AD⊥BC于点D ，若 $\frac{B D}{C D}$ ＝ $\frac{4}{3}$ ．则tanC的值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3 \sqrt{3}}{4}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
8. 如图，在△ABC中，∠C＝90°，AC＝12，AB的垂直平分线EF交AC于点D，连接BD，若cos∠BDC＝ $\frac{5}{7}$ ，则BC的长是（）

A、10 B、8 C、4 $\sqrt{3}$ D、2 $\sqrt{6}$

查看试题解析
9. 如图，边长为10的等边 $△ A B C$ 中，点 $D$ 在边 $A C$ 上，且 $A D = 3$ ，将含30°角的直角三角板（ $∠ F = 30 °$ ）绕直角顶点 $D$ 旋转， $D E$ 、 $D F$ 分别交边 $A B$ 、 $B C$ 于 $P$ 、 $Q$ .连接 $P Q$ ，当 $E F / / P Q$ 时， $D Q$ 长为（）

A、6 B、 $\sqrt{39}$ C、10 D、 $6 \sqrt{3}$

查看试题解析
10. 如图，△ABC中，AB=AC= $2 \sqrt{5}$ ，∠BAC=α°， $\tan ∠ A B C = \frac{1}{2}$ ，G为BC中点，D为平面内一个动点，且 $D G = \frac{\sqrt{5}}{5}$ .将线段BD绕点D逆时针旋转α°，得到DB′，则四边形BACB′面积的最大值为（）

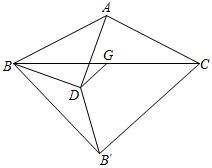A、24 B、25 C、12 D、13

查看试题解析

二、填空题

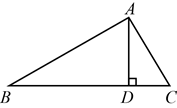
11. 已知△ABC中，∠ABC＝90°，如果AC＝5，sinA＝ $\frac{3}{5}$ ，那么AB的长是．

查看试题解析
12. 已知 $∠ A ， ∠ B ， ∠ C$ 是 $Δ A B C$ 的三个内角，若 $| s i n A - \frac{\sqrt{3}}{2} | + {(c o s B - \frac{\sqrt{2}}{2})}^{2} = 0$ ，且 $∠ A ， ∠ B$ 均为锐角，则 $∠ C$ 的度数为.

查看试题解析
13. 如图，已知Rt $△$ ABC中，斜边BC上的高AD＝4，cosB $= \frac{4}{5}$ ，则AC＝.

查看试题解析
14. 如图，边长为1的小正方形构成的网格中，半径为1的⊙O在格点上，则∠AED的正切值为．

查看试题解析
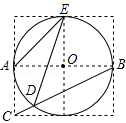15. 如图，AB为半圆O的直径，点C为半圆上的一点，CD⊥AB于点D，若AB=10，CD=4，则sin∠BCD的值为．

查看试题解析
16. 如图，已知扇形OAB的半径为6，C是弧AB上的任一点（不与A，B重合），CM⊥OA，垂足为M，CN⊥OB，垂足为N，连接MN，若∠AOB＝45°，则MN＝.

查看试题解析
17. 如图，在边长相同的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB，CD相交于点P，则 $\frac{A P}{P B}$ 的值= ， tan∠APD的值= ．

查看试题解析
18. 如图，二次函数 $y = - x^{2} + 2 x + 3$ 的图象与x轴交于A，B两点，与y轴交于点C，对称轴与x轴交于点D，若点P为y轴上的一个动点，连接PD，则 $\frac{\sqrt{10}}{10} P C + P D$ 的最小值为.

查看试题解析

三、解答题

19. 计算题

(1)、 $\cos^{2} 45 ° - 4 \sin 30 ° + {(\frac{1}{7})}^{- 1} - {(π - 3.14)}^{0}$ ；

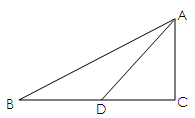
(2)、已知 $α$ 是锐角，且 $\sin (α + 15 °) = \frac{\sqrt{3}}{2}$ ，计算 $\sqrt{8} - 4 \cos α - | 1 - 2 \sin α | + \tan α$ 的值．

查看试题解析
20. 如图，在Rt△ABC中，∠C=90°，sinB= $\frac{5}{13}$ ，D在BC边上，且∠ADC=45°，AC=5．求∠BAD的正切值．

查看试题解析
21. 已知四边形ABCD是⊙O的内接四边形，∠DAB＝120°，BC＝CD ， AD＝4，AC＝7，求AB的长度．

查看试题解析
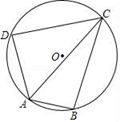22. 如图，在矩形ABCD中，AB＝3，AD＝5，点E在DC上，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，求cos∠EFC的值．

查看试题解析
23. 如图，在△ABC中，CD是AB边上的中线，∠B＝45°，tan∠ACB＝3，AC＝ $\sqrt{10}$ .
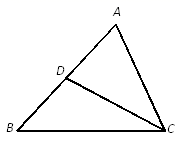
求：

(1)、△ABC的面积；

(2)、sin∠ACD的值．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ，点E在BC边上，过A，C，E三点的 $⊙ O$ 交AB边于另一点F，且F是弧AE的中点，AD是 $⊙ O$ 的一条直径，连接DE并延长交AB边于M点.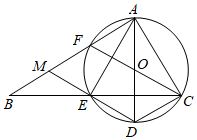

(1)、求证：四边形CDMF为平行四边形；

(2)、当 $C D = \frac{2}{5} A B$ 时，求 $\sin ∠ A C F$ 的值.

查看试题解析
25. 如图1，AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线，过点A作AE⊥AD，交BD的延长线于点E.

(1)、求证：∠E= $\frac{1}{2}$ ∠C；

(2)、如图2，如果AE=AB，且BD：DE=2：3，求cos∠ABC的值；

(3)、如果∠ABC是锐角，且△ABC与△ADE相似，求∠ABC的度数.

查看试题解析
26. 在Rt△ABC中，∠BAC=90°，过点B的直线MN∥AC，D为BC边上一点，连接AD，作DE⊥AD交MN于点E，连接AE.

(1)、如图①，当∠ABC=45°时，求证：AD=DE；并说明理由；

(2)、如图②，当∠ABC=30°时，线段AD与DE有何数量关系？并请说明理由；

(3)、当∠ABC=α时，请直接写出线段AD与DE的数量关系.（用含α的三角函数表示）

查看试题解析

2022年苏科版初中数学《中考一轮复习》专题五 图形的变换 5.6 锐角三角函数

一、单选题

二、填空题

三、解答题

2022年苏科版初中数学《中考一轮复习》专题五图形的变换 5.6 锐角三角函数