湘教版初中数学九年级下册1.5抛物线的应用同步练习

试卷更新日期：2022-02-10 类型：同步测试

进入出卷网下载

一、单选题

1. 小敏在某次投篮中，篮球的运动路线是抛物线 $y = - \frac{1}{5} x^{2} +$ 3.5的一部分（如图），若命中篮圈中心，则他与篮底的水平距离 $l$ 是（）

A、3.5m B、3.8m C、4m D、4.5m

查看试题解析
2. 一位运动员在离篮筐水平距离4m处起跳投篮，球运行路线可看作抛物线，当球离开运动员的水平距离为1m时，它与篮筐同高，球运行中的最大高度为3.5m，最后准确落入篮筐，已知篮筐到地面的距离为3.05m，该运动员投篮出手点距离地面的高度为（）

A、1.5m B、2m C、2.25m D、2.5m

查看试题解析
3. 在平面直角坐标系中，已知点M，N的坐标分别为 $(- 1 ， 3) ， (3 ， 3)$ ，若抛物线 $y = x^{2} - 2 m x + m^{2} - m + 2$ 与线段MN只有一个公共点，则 $m$ 的取值范围是（）

A、 $- 1 ⩽ m < 0$ 或 $\frac{7 - \sqrt{17}}{2} < m ⩽ \frac{7 + \sqrt{17}}{2}$ B、 $- 1 ⩽ m < 0$ 或 $m > \frac{7 - \sqrt{17}}{2}$ C、 $m < 0$ 或 $\frac{7 - \sqrt{17}}{2} < m ⩽ \frac{7 + \sqrt{17}}{2}$ D、 $- 1 ⩽ m ⩽ \frac{7 + \sqrt{17}}{2}$

查看试题解析
4. 如图，在平面直角坐标系中放置 $Rt △ A B C ， ∠ A B C = 90^{\circ}$ ，点 $A (3 ， 4)$ .现将 $△ A B C$ 沿 $x$ 轴的正方向无滑动翻转，依次得到 $△ A_{1} B_{1} C_{1} ， △ A_{2} B_{2} C_{2} ， △ A_{3} B_{3} C_{3} \dots$ 连续翻转 14 次，则经过 $△ A_{14} B_{14} C_{14}$ 三顶点的抛物线解析式为（）

A、 $y = - \frac{3}{5} (x - 51) (x - 55)$ B、 $y = - \frac{5}{12} (x - 51) (x - 55)$ C、 $y = - \frac{3}{5} (x - 55) (x - 60)$ D、 $y = - \frac{5}{12} (x - 55) (x - 60)$

查看试题解析
5. 如图，正六边形的边长为10，分别以正六边形的顶点A、B、C、D、E、F为圆心，画6个全等的圆．若圆的半径为x，且0＜x≤5，阴影部分的面积为y，能反映y与x之间函数关系的大致图形是（）

A、 B、 C、 D、

查看试题解析
6. 某建筑物，从10m高的窗口A，用水管向外喷水，喷出的水呈抛物线状（抛物线所在的平面与墙面垂直），如图所示，如果抛物线的最高点M离墙1m，离地面 $\frac{40}{3}$ m，则水流落地点B离墙的距离OB是（）

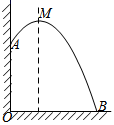A、2m B、3m C、4m D、5m

查看试题解析
7. 如图，函数 $y = - x^{2} + 12$ 的图象与x轴交于A，B两点，点C是以 $M (0 ， 2)$ 为圆心，2为半径的圆上的动点，P是 $A C$ 的中点，连结 $O P$ ，则线段 $O P$ 的最小值是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{7}$

查看试题解析
8. 有一拱桥洞呈抛物线形，这个桥洞的最大高度是16m，跨度为40m，现把它的示意图(如图)放在坐标系中，则抛物线的解析式为（）

A、y＝ $\frac{1}{25}$ x²＋ $\frac{5}{8}$ x B、y＝－ $\frac{1}{25}$ x²＋ $\frac{8}{5}$ x C、y＝－ $\frac{5}{8}$ x²－ $\frac{1}{25}$ x D、y＝－ $\frac{1}{25}$ x²＋ $\frac{8}{5}$ x＋16

查看试题解析
9. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（）

A、此抛物线的解析式是y＝﹣ $\frac{1}{5}$ x²+3.5 B、篮圈中心的坐标是（4，3.05） C、此抛物线的顶点坐标是（3.5，0） D、篮球出手时离地面的高度是2m

查看试题解析
10. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB＝m.若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为（）

A、193 B、194 C、195 D、196

查看试题解析

11. 足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如表：

t	0	1	2	3	4	5	6	7	…
h	0	8	14	18	20	20	18	14	…

下列结论：①足球距离地面的最大高度超过20m；②足球飞行路线的对称轴是直线t＝ $\frac{9}{2}$ ；③点（9，0）在该抛物线上；④足球被踢出5s～7s时，距离地面的高度逐渐下降.其中正确的结论是（）

A、②③ B、①②③ C、①②③④ D、②③④

查看试题解析

12. 如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动，同时点Q沿边AB，BC从点A开始向点C以2cm/s的速度移动，当点P移动到点A时，P、Q同时停止移动。设点P出发x秒时，△PAQ的面积为ycm² ， y与x的函数图象如图②，则下列四个结论，其中正确的有（）个
①当点P移动到点A时，点Q移动到点C ②正方形边长为6cm ③当AP=AQ时，△PAQ面积达到最大值④线段EF所在的直线对应的函数关系式为y=−3x+18

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 如图，Rt△ABC中，∠ACB=90°，AC=BC=2，点P是AB上一动点，连接CP，将线段CP绕点C顺时针旋转90°得到线段CQ，连接PQ，AQ，则△PAQ面积的最大值为.

查看试题解析
14. 如图，在平面直角坐标系中，抛物线y=(x-2)²与x轴交于点A，与y轴交于点B，过点B作BC∥x轴，交抛物线于点C，过点A作AD∥y轴，交BC于点D，点P在BC下方的抛物线上(不与点B，C重合)，连接PC，PD，设△PCD的面积为S，则S的最大值是．

查看试题解析
15. 如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加m.

查看试题解析
16. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程，它是一条经过A、M、C三点的抛物线．其中A点离地面1.4米，M点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是球落地时的第一点．那么足球第一次落地点C距守门员的水平距离为米．

查看试题解析
17. 某电商平台11月1日起开始销售一款新品牌手机，当月的日销售额y（万元）和销售时间第x天（1≤x≤30且x为整数）之间满足二次函数关系y=-（x-h）+k，根据市场调查可以确定在当月中旬日销售额达到最大值．

(1)、若第18天的销售额比第19天的销售额多5万元，则第天的日销售额最大；

(2)、若第18天后的日销售额呈下降趋势，则h的取值范围是

查看试题解析
18. 如图，拱桥的形状是抛物线，其函数关系式为 $y = - \frac{1}{3} x^{2}$ ，当水面离桥顶的高度为 $\frac{25}{3}$ 米时，水面的宽度为米.

查看试题解析

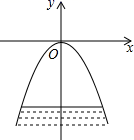
三、解答题

19. 如图是抛物线形拱桥，当水面宽为4米时，拱顶距离水面2米；当水面高度下降1米时，水面宽度为多少米？请你以点D为原点、 $A B$ 所在直线为x轴建立平面直角坐标系，解决这个实际问题．

查看试题解析
20. 现要用60米长的篱笆围成一个矩形场地（一边靠墙且墙长40米），应怎样围才能使矩形的面积S最大？最大是多少？

查看试题解析
21. 某民俗旅游村为接待游客住宿需要，开设了有100张床位的旅馆，当每张床位每天收费80元时，床位可全部租出，若每张床位每天收费提高10元，则相应的减少了10张床位租出，如果每张床位每天以10元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天应提高多少元？

查看试题解析

四、综合题

22. 我市绿色和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地.上市时，外贸商李经理按市场价格10元/千克在我市收购了2000千克香菇存放入冷库中.请根据李经理提供的预测信息（如下图）帮李经理解决以下问题：

(1)、若存放 $x$ 天后，将这批香菇一次性出售，设这批香菇的销售总金额为 $y$ 元，试写出 $y$ 与 $x$ 之间的函数表达式；（销售总金额=销售单价×销售量）

(2)、将这批香菇仔放多少天后出售可获得最大利润?最大利润是多少?

查看试题解析

23. 在“新冠”疫情期间，全国人民“众志成城，同心抗疫”，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品，成本为10元/件，拟采取线上和线下两种方式进行销售.调查发现，线下的月销量

y

（单位：件）与线下售价

x

（单位：元/件，

12 \leq x < 24

）满足一次函数的关系，部分数据如下表：

x（元/件）	12	13	14	15	16
y（件）	1200	1100	1000	900	800

(1)、求

y

与

x

的函数关系式；

(2)、若线上售价始终比线下每件便宜2元，且线上的月销量固定为400件.试问：当

x

为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润.

查看试题解析

24. 某商场销售一批衬衫，进货价为每件30元，按每件50元出售，一个月内可售出500件．已知这种衬衫每件涨价1元，其销售量要减少10件，

(1)、要在一个月内赚取12000元的利润，同时为了减少库存，售价应定为每件多少元？

(2)、要想一个月内获得的利润最大，该商场应当如何定价销售？

查看试题解析