湘教版初中数学九年级下册1.3不共线三点确定二次函数的表达式同步练习

试卷更新日期：2022-02-10 类型：同步测试

进入出卷网下载

一、单选题

1. 已知二次函数 $y = a x^{2} + x + a (a - 2)$ 的图象经过原点，则a的值为（）

A、0或2 B、0 C、2 D、无法确定

查看试题解析
2. 已知二次函数 $y = (a - 1) x^{2} - x + a^{2} - 1$ 图象经过原点，则a的取值为（）．

A、 $a = \pm 1$ B、 $a = 1$ C、 $a = - 1$ D、 $a = 0$

查看试题解析
3. 一个二次函数的图象的顶点坐标是 $(2 ， - 3)$ ，与y轴的交点是 $(0 ， 5)$ ，这个二次函数的解析式是（）

A、 $y = 2 x^{2} - 4 x + 11$ B、 $y = 2 x^{2} - 4 x + 5$ C、 $y = 2 x^{2} - 8 x + 5$ D、 $y = 2 x^{2} + 8 x + 5$

查看试题解析
4. 二次函数的图象如图所示，则这个二次函数的表达式为（）

A、 $y = x^{2} + 2 x - 3$ B、 $y = x^{2} - 2 x - 3$ C、 $y = - x^{2} + 2 x - 3$ D、 $y = - x^{2} - 2 x + 3$

查看试题解析
5. 顶点为 $(6 ， 0)$ ，开口向下，开口的大小与函数 $y = \frac{1}{3} x^{2}$ 的图象相同的抛物线所对应的函数是（）

A、 $y = \frac{1}{3} {(x + 6)}^{2}$ B、 $y = \frac{1}{3} {(x - 6)}^{2}$ C、 $y = - \frac{1}{3} {(x + 6)}^{2}$ D、 $y = - \frac{1}{3} {(x - 6)}^{2}$

查看试题解析
6. 如图，是一条抛物线的图象，则其解析式为（　　）

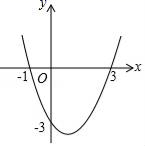A、y=x²﹣2x+3 B、y=x²﹣2x﹣3 C、y=x²+2x+3 D、y=x²+2x-3

查看试题解析
7. 已知某二次函数的图象如图所示，则这个二次函数的解析式为（）

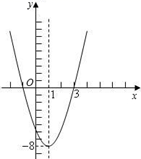A、 $y = 2 {(x + 1)}^{2} + 8$ B、 $y = 18 {(x + 1)}^{2} - 8$ C、 $y = \frac{2}{9} {(x - 1)}^{2} + 8$ D、 $y = 2 {(x - 1)}^{2} - 8$

查看试题解析
8. 若抛物线经过 $(0 ， 1) ， (- 1 ， 0) ， (1 ， 0)$ 三点，则此抛物线的表达式为（）

A、 $y = - x^{2} + 1$ B、 $y = - x^{2} - 1$ C、 $y = x^{2} + 1$ D、 $y = x^{2} - 1$

查看试题解析
9. 已知二次函数y=mx²+x+m（m-2）的图像经过原点，则m的值为（）

A、0或2 B、0 C、2 D、无法确定

查看试题解析
10. 记某商品销售单价为x元，商家销售此种商品每月获得的销售利润为y元，且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时，他每月均可获得销售利润1800元；当商家将此种商品销售单价定为80元时，他每月可获得销售利润1550元，则y与x的函数关系式是（）

A、y＝﹣（x﹣60）²+1825 B、y＝﹣2（x﹣60）²+1850 C、y＝﹣（x﹣65）²+1900 D、y＝﹣2（x﹣65）²+2000

查看试题解析
11. 2019年女排世界杯于9月在日本举行，中国女排以十一连胜的骄人成绩卫冕冠军，充分展现了团队协作、顽强拼搏的女排精神．如图是某次比赛中垫球时的动作．若将垫球后排球的运动路线近似的看作抛物线，在同一竖直平面内建立如图所示的直角坐标系，已知运动员垫球时（图中点A）离球网的水平距离为5米，排球与地面的垂直距离为0.5米，排球在球网上端0.26米处（图中点B）越过球网（女子排球赛中球网上端距地面的高度为2.24米），落地时（图中点C）距球网的水平距离为2.5米，则排球运动路线的函数表达式为（）

A、y＝﹣ $\frac{14}{75} x^{2} - \frac{8}{15} x + \frac{5}{2}$ B、y＝﹣ $\frac{14}{75} x^{2} + \frac{8}{15} x + \frac{5}{2}$ C、y＝ $\frac{14}{75} x^{2} - \frac{8}{15} x + \frac{5}{2}$ D、y＝ $\frac{14}{75} x^{2} + \frac{8}{15} x + \frac{5}{2}$

查看试题解析
12. 抛物线y＝ax²+bx﹣3与x轴交于A ， B两点，与y轴交于点C ，且OB＝OC＝3OA ，求抛物线的解析式（）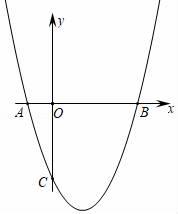

A、y＝x²﹣2x﹣3 B、y＝x²﹣2x+3 C、y＝x²﹣2x﹣4 D、y＝x²﹣2x﹣5

查看试题解析

二、填空题

13. 若二次函数 $y = x^{2} + 3 x$ 的图象经过点 $P (2 ， a)$ ，则 $a$ 的值为.

查看试题解析
14. 已知抛物线的顶点坐标为(4，−1)，与y轴交于点(0，3)，则这条抛物线的解析式是.

查看试题解析
15. 如图，抛物线y＝ax²﹣x﹣ $\frac{3}{2}$ 与x轴正半轴交于点A（3，0）．以OA为边在x轴上方作正方形OABC ，延长CB交抛物线于点D ，再以BD为边向上作正方形BDEF ．

(1)、a的值为；

(2)、点F的坐标是．

查看试题解析
16. 请写出一个与y轴交点为（0，5），对称轴为直线x=-1的抛物线的解析式（只需写一个）．

查看试题解析
17. 若二次函数顶点坐标为 $(2 ， 3)$ ，且过点 $(1 ， 5)$ ，则二次函数解析式为

查看试题解析
18. 请你写出一个抛物线使它满足以下条件：（1）开口向下，（2）顶点坐标为（1，3），则这个抛物线的表达式是．

查看试题解析
19. 试写出一个抛物线，它的开口向上，且对称轴是直线x＝1：．

查看试题解析
20. 请写出一个开口向上，且经过点（0，-1）的抛物线解析式：
（只需写一个）

查看试题解析

三、解答题

21. 已知抛物线过点A（－1，0），B（0，6），对称轴为直线x＝1，求该抛物线的解析式．

查看试题解析
22. 若抛物线的顶点坐标是A（1，－4），并且抛物线经过点B坐标为（3，－2）.求出该抛物线的关系式.

查看试题解析
23. 一条抛物线经过点A(-2，0)且抛物线的顶点是(1，－3)，求满足此条件的函数解析式．

查看试题解析

四、综合题

24. 若二次函数 $y = {ax}^{2} + bx + c$ 的x与y的部分对应值如下表：

x

-1

0

1

2

3

4

y

0

3

4

3

0

-5

(1)、求这个二次函数的表达式；

(2)、当x=﹣2时，y的值.

查看试题解析

25. 二次函数

y = a x^{2} + b x + c

（a，b，c是常数，

a \neq 0

）的自变量x与函数值y的部分对应值如下表：

x	…	$- 3$	$- 2$	$- 1$	0	1	…
$y = a x^{2} + b x + c$	…	$\frac{5}{2}$	4	$\frac{9}{2}$	4	m	…

根据以上列表，回答下列问题：

(1)、直接写出c，m的值；

(2)、求此二次函数的解析式．

查看试题解析

26. 已知二次函数的图象过顶点（8，9），且其图象过点（0，1）

(1)、求二次函数的解析式．

(2)、判断点A(16，1)是否在此二次函数的图象上？

查看试题解析