备考2022届中考数学全国精选题汇编专题4 数与式及其拓展

试卷更新日期：2022-02-10 类型：一轮复习

进入出卷网下载

一、单选题

1. 小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 $y = k_{n} x + b_{n} (n = 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7)$ ，其中 $k_{1} = k_{2} ， b_{3} = b_{4} = b_{5}$ ，则他探究这7条直线的交点个数最多是（）

A、17个 B、18个 C、19个 D、21个

查看试题解析
2. 定义： $\min {a ， b} = {\begin{array}{l} a (a \leq b) \\ b (a > b) \end{array}$ ，若函数 $y = \min (x + 1 ， - x^{2} + 2 x + 3)$ ，则该函数的最大值为（）

A、0 B、2 C、3 D、4

查看试题解析
3. 如 $M = {1 ， 2 ， x}$ ，我们叫集合 $M$ ，其中1，2， $x$ 叫做集合 $M$ 的元素.集合中的元素具有确定性（如 $x$ 必然存在），互异性（如 $x \neq 1$ ， $x \neq 2$ ），无序性（即改变元素的顺序，集合不变）.若集合 $N = {x ， 1 ， 2}$ ，我们说 $M = N$ .已知集合 $A = {1 ， 0 ， a}$ ，集合 $B = {\frac{1}{a} ， | a | ， \frac{b}{a}}$ ，若 $A = B$ ，则 $b - a$ 的值是（）

A、－1 B、0 C、1 D、2

查看试题解析
4. 将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）

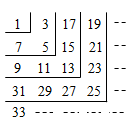A、2025 B、2023 C、2021 D、2019

查看试题解析
5. 下列计算正确的是（）

A、 ${(a^{3})}^{3} = a^{9}$ B、 $a^{3} \cdot a^{4} = a^{12}$ C、 $a^{2} + a^{3} = a^{5}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
6. 下列无理数，与3最接近的是（）

A、 $\sqrt{6}$ B、 $\sqrt{7}$ C、 $\sqrt{10}$ D、 $\sqrt{11}$

查看试题解析
7. 下列计算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $a^{3} \cdot a^{3} = a^{6}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 ${(a b)}^{3} = a b^{3}$

查看试题解析
8. 如图，已知数轴上 $A ， B$ 两点表示的数分别是 $a ， b$ ，则计算 $| b | - | a |$ 正确的是（）

A、 $b - a$ B、a-b C、 $a + b$ D、 $- a - b$

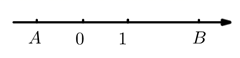查看试题解析
9. 下列运算正确的是（）

A、 ${(3 - π)}^{0} = - 1$ B、 $\sqrt{9} = \pm 3$ C、 $3^{- 1} = - 3$ D、 ${(- a^{3})}^{2} = a^{6}$

查看试题解析
10. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $a^{3} a^{2} = α^{6}$ C、 ${(a^{3})}^{2} = a^{6}$ D、 $a^{2} － b^{2} = {(a - b)}^{2}$

查看试题解析
11. 下列运算正确的是（）

A、 ${(- x^{3})}^{2} = x^{5}$ B、 $\sqrt{{(- x)}^{2}} = x$ C、 ${(- x)}^{2} + x = x^{3}$ D、 ${(- 1 + x)}^{2} = x^{2} - 2 x + 1$

查看试题解析
12. 下列计算正确的是（）

A、a²+a²＝2a⁴ B、a²⋅a＝a³ C、（3a）²＝6a² D、a⁶+a²＝a³

查看试题解析
13. 若a＝ $\sqrt[3]{7}$ ，b＝ $\sqrt{5}$ ，c＝2，则a、b、c的大小关系为（）

A、b＜c＜a B、b＜a＜c C、a＜c＜b D、a＜b＜c

查看试题解析
14. 下列数中，在 $\sqrt[3]{80}$ 与 $\sqrt[3]{200}$ 之间的是（）

A、3 B、4 C、5 D、6

查看试题解析
15. 计算 $\sqrt{18} \times \sqrt{12}$ 的结果是（）

A、6 B、 $6 \sqrt{2}$ C、 $6 \sqrt{3}$ D、 $6 \sqrt{6}$

查看试题解析
16. 整式 $- 3 x y^{2}$ 的系数是（）

A、-3 B、3 C、 $- 3 x$ D、 $3 x$

查看试题解析

二、填空题

17. 古希腊数学家把1，3，6，10，15，21，…这样的数叫做三角形数，因为它的规律性可以用如图表示.根据图形，若把第一个图形表示的三角形数记为 $a_{1} = 1$ ，第二个图形表示的三角形数记为 $a_{2} = 3$ ，…，则第 $n$ 个图形表示的三角形数 $a_{n}$ ＝.（用含 $n$ 的式子表达）

查看试题解析
18. 如图，将正整数按此规律排列成数表，则2021是表中第行第列.

查看试题解析
19. 观察下列各项： $1 \frac{1}{2}$ ， $2 \frac{1}{4}$ ， $3 \frac{1}{8}$ ， $4 \frac{1}{16}$ ，…，则第 $n$ 项是.

查看试题解析
20. 因式分解：x²－36= .

查看试题解析
21. 若式子 $\frac{2}{y - 2} + 1$ 的值为零，则 $y$ ＝.

查看试题解析
22. 计算： $| 1 - \sqrt{2} | + {(\frac{1}{2})}^{- 1} + 2 \cos 45 ° + {(- 1)}^{0} =$ .

查看试题解析
23. 分解因式： $4 a x^{2} - 4 a y^{2} =$ .

查看试题解析
24. 把多项式 $x^{3} + 2 x^{2} - 3 x$ 因式分解，结果为.

查看试题解析
25. 若 $x - y = \sqrt{3}$ ， $x y = - \frac{3}{4}$ ，则 $x^{2} - y^{2} =$ .

查看试题解析
26. 据统计，截止2021年3月，中国共产党党员人数超过9100万.数字91000000用科学记数法表示为.

查看试题解析

三、计算题

27. 计算：

(1)、 $| - 2 | - 2021^{0} + \sqrt[3]{8} - {(\frac{1}{2})}^{- 1}$

(2)、 $(1 + \frac{2 a + 1}{a^{2}}) \div \frac{a + 1}{a}$

查看试题解析
28.

(1)、化简求值： ${(2 x - 1)}^{2} + (x + 6) (x - 2)$ ，其中 $x = - \sqrt{3}$ ；

(2)、解方程 $\frac{2}{x - 3} - \frac{3}{x} = 0$ .

查看试题解析
29. 计算： ${(- 2)}^{0} - \sqrt{8} - | - 5 | + 4 \sin 45 °$ .

查看试题解析
30. 先化简，再求值： $\frac{a^{2} - b^{2}}{a} \div (a - \frac{2 a b - b^{2}}{a})$ ，其中 $a = 2$ ， $b = 1$ .

查看试题解析
31.

(1)、计算： $2 \cos 30 ° - 2^{- 1} - \sqrt{12} - | \sqrt{3} - 2 | + {(3.14 - π)}^{0}$

(2)、先化简： $\frac{x^{2} + 3 x}{x^{2} - 4 x + 4} \div \frac{x + 3}{x - 2} \cdot \frac{x^{2} - 4}{x}$ ，然后 $x$ 从0、1、2三个数中选一个你认为合适的数代入求值.

查看试题解析
32. 先化简，再求值： $\frac{x}{x - 4} \cdot (\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4})$ ，其中 $x = 3 - \sqrt{2}$ .

查看试题解析
33. 先化简，再求值：（ $\frac{x^{2} + 2 x + 1}{x^{2} - 1}$ ﹣ $\frac{1}{x - 1}$ ）÷ $\frac{x^{2}}{x - 1}$ ，其中x﹣3＝0.

查看试题解析
34. 计算：|﹣3|+（﹣2）².

查看试题解析

四、综合题

35. 数学课外活动小组的同学在学习了完全平方公式之后，针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究，请阅读以下探究过程并解决问题.
猜想发现：由 $5 + 5 = 2 \sqrt{5 \times 5} = 10$ ； $\frac{1}{3} + \frac{1}{3} = 2 \sqrt{\frac{1}{3} \times \frac{1}{3}} = \frac{2}{3}$ ； $0.4 + 0.4 = 2 \sqrt{0.4 \times 0.4} = 0.8$ ； $\frac{1}{5} + 5 > 2 \sqrt{\frac{1}{5} \times 5} = 2$ ； $0.2 + 3.2 > 2 \sqrt{0.2 \times 3.2} = 1.6$ ； $\frac{1}{2} + \frac{1}{8} > 2 \sqrt{\frac{1}{2} \times \frac{1}{8}} = \frac{1}{2}$

猜想：如果 $a > 0$ ， $b > 0$ ，那么存在 $a + b \geq 2 \sqrt{a b}$ （当且仅当 $a = b$ 时等号成立）.

猜想证明：∵ ${(\sqrt{a} - \sqrt{b})}^{2} \geq 0$

∴①当且仅当 $\sqrt{a} - \sqrt{b} = 0$ ，即 $a = b$ 时， $a - 2 \sqrt{a b} + b = 0$ ，∴ $a + b = 2 \sqrt{a b}$ ；

②当 $\sqrt{a} - \sqrt{b} \neq 0$ ，即 $a \neq b$ 时， $a - 2 \sqrt{a b} + b > 0$ ，∴ $a + b > 2 \sqrt{a b}$ .

综合上述可得：若 $a > 0$ ， $b > 0$ ，则 $a + b \geq 2 \sqrt{a b}$ 成立（当日仅当 $a = b$ 时等号成立）.

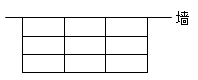
(1)、猜想运用：对于函数 $y = x + \frac{1}{x} (x > 0)$ ，当x取何值时，函数y的值最小？最小值是多少？

(2)、变式探究：对于函数 $y = \frac{1}{x - 3} + x (x > 3)$ ，当x取何值时，函数y的值最小？最小值是多少？

(3)、
拓展应用：（3）疫情期间、为了解决疑似人员的临隔离问题.高速公路榆测站入口处，检测人员利用检测站的一面墙（墙的长度不限），用63米长的钢丝网围成了9间相同的长方形隔离房，如图.设每间离房的面积为S（米²）.问：每间隔离房的长、宽各为多少时，可使每间隔离房的面积S最大？最大面积是多少？

查看试题解析
36. 在平面直角坐标系 $x O y$ 中， $⊙ O$ 的半径为1，对于点 $A$ 和线段 $B C$ ，给出如下定义：若将线段 $B C$ 绕点 $A$ 旋转可以得到 $⊙ O$ 的弦 $B^{'} C^{'}$ （ $B^{'} ， C^{'}$ 分别是 $B ， C$ 的对应点），则称线段 $B C$ 是 $⊙ O$ 的以点 $A$ 为中心的“关联线段”．

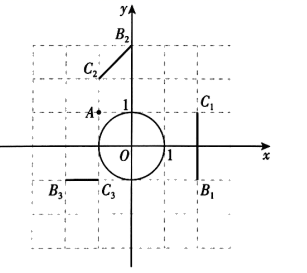(1)、如图，点 $A ， B_{1} ， C_{1} ， B_{2} ， C_{2} ， B_{3} ， C_{3}$ 的横､纵坐标都是整数．在线段 $B_{1} C_{1} ， B_{2} C_{2} ， B_{3} C_{3}$ 中， $⊙ O$ 的以点 $A$ 为中心的“关联线段”是；

(2)、 $△ A B C$ 是边长为1的等边三角形，点 $A (0 ， t)$ ，其中 $t \neq 0$ ．若 $B C$ 是 $⊙ O$ 的以点 $A$ 为中心的“关联线段”，求 $t$ 的值；

(3)、在 $△ A B C$ 中， $A B = 1 ， A C = 2$ ．若 $B C$ 是 $⊙ O$ 的以点 $A$ 为中心的“关联线段”，直接写出 $O A$ 的最小值和最大值，以及相应的 $B C$ 长．

查看试题解析
37. 已知抛物线 $y = - 2 x^{2} + b x + c$ 经过点 $(0 ， - 2)$ ，当 $x < - 4$ 时，y随x的增大而增大，当 $x > - 4$ 时，y随x的增大而减小．设r是抛物线 $y = - 2 x^{2} + b x + c$ 与x轴的交点（交点也称公共点）的横坐标， $m = \frac{r^{9} + r^{7} - 2 r^{5} + r^{3} + r - 1}{r^{9} + 60 r^{5} - 1}$ ．

(1)、求b、c的值：

(2)、求证： $r^{4} - 2 r^{2} + 1 = 60 r^{2}$ ；

(3)、以下结论： $m < 1 ， m = 1 ， m > 1$ ，你认为哪个符合题意？请证明你认为正确的那个结论．

查看试题解析
38.

(1)、分解因式：x³﹣9x；

(2)、解方程： $\frac{2 x}{x - 2}$ +1＝ $\frac{5}{2 - x}$ .

查看试题解析
39.

(1)、有三个不等式 $2 x + 3 〈 - 1 ， - 5 x 〉 15 ， 3 (x - 1) > 6$ ，请在其中任选两个不等式，组成一个不等式组，并求出它的解集：

(2)、小红在计算 $a (1 + a) - {(a - 1)}^{2}$ 时，解答过程如下：
$a (1 + a) - {(a - 1)}^{2}$

$= a + a^{2} - (a^{2} - 1)$ 第一步

$= a + a^{2} - a^{2} - 1$ 第二步

$= a - 1$ 第三步

小红的解答从第 ▲ 步开始出错，请写出正确的解答过程.

查看试题解析
40.

(1)、计算： $2 \cos 45 ° + | \sqrt{2} - \sqrt{3} | - 2021^{0} - \frac{3}{\sqrt{3}}$ ；

(2)、先化简，再求值： $\frac{2}{x - y} - \frac{x}{x + y} - \frac{2 x y}{x^{2} - y^{2}}$ ，其中 $x = 1.12$ ， $y = 0.68$ .

查看试题解析