备考2022届中考数学全国精选题汇编专题1 锐角三角函数的定义及应用
试卷更新日期:2022-02-09 类型:一轮复习
一、单选题
-
1. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
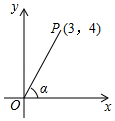 A、 B、 C、 D、2. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A、 B、 C、 D、2. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
3. 如图,在△ABC中,AB=5,AC=4,sinA= ,BD⊥AC交AC于点D.点P为线段BD上的动点,则PC+ PB的最小值为 .
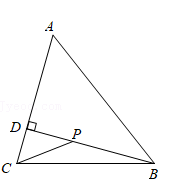 4. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.
4. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.三、综合题
-
5. 如图, 为⊙ 的直径, 为⊙O上一点, 和过点 的切线互相垂直,垂足为 .
 (1)、求证: 平分 ;(2)、若 , ,求:边 及 的长.6. 如图,在 中, ,点E在BC边上,过A,C,E三点的 交AB边于另一点F,且F是弧AE的中点,AD是 的一条直径,连接DE并延长交AB边于M点.
(1)、求证: 平分 ;(2)、若 , ,求:边 及 的长.6. 如图,在 中, ,点E在BC边上,过A,C,E三点的 交AB边于另一点F,且F是弧AE的中点,AD是 的一条直径,连接DE并延长交AB边于M点.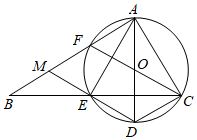 (1)、求证:四边形CDMF为平行四边形;(2)、当 时,求 的值.7. 如图,PA是以AC为直径的☉O的切线,切点为A,过点A作AB⊥OP,交☉O于点B.
(1)、求证:四边形CDMF为平行四边形;(2)、当 时,求 的值.7. 如图,PA是以AC为直径的☉O的切线,切点为A,过点A作AB⊥OP,交☉O于点B.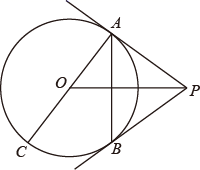 (1)、求证:PB是☉O的切线;(2)、若AB=6, ,求PO的长.8. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .
(1)、求证:PB是☉O的切线;(2)、若AB=6, ,求PO的长.8. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .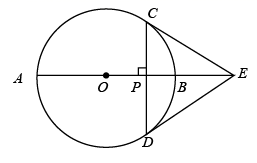 (1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .9. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .9. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.

