2021-2022学年浙教版数学七下2.2 二元一次方程组同步练习
试卷更新日期:2022-01-28 类型:同步测试
一、单选题
-
1. 下到方程组中,属于二元一次方程组的是( )A、 B、 C、 D、2. 已知关于x,y的方程组 的解为 ,则关于方程组 的解为( )A、 B、 C、 D、3. 已知x,y满足方程组 ,则无论m取何值,x,y恒有关系式( )A、x+y=3 B、x+y=﹣3 C、x+y=9 D、x+y=﹣94. 已知 是二元一次方程mx+3y=7的一组解,则m的值为( )A、﹣2 B、2 C、﹣ D、5. 与方程5x+2y=-9构成的方程组,其解为 的是( )A、x+2y=1 B、3x+2y=-8 C、3x-4y=-8 D、5x+4y=-36. 下列方程组中,不属于二元一次方程组的是( )A、 B、 C、 D、7. 在方程组 、 、 、 、 、 中,是二元一次方程组的有( )A、2个 B、3个 C、4个 D、5个8. 方程组 的解为( )A、 B、 C、 D、9. 小轩解方程组 的解为 ,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则两个数●与★的值分别为( )A、 B、 C、 D、10. 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知关于x、y的二元一次方程组 的解为 ,则a+b的值为 .12. 是某个二元一次方程组的解,则这个方程组是.13. 若方程组 是关于x,y的二元次方程组,则代数式a+b+c=.14. 已知方程 是关于 , 的二元一次方程,则 = .15. 古代算筹图用图1表示方程组: ,请写出图2所表示的二元一次方程组 .
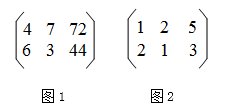 16. 在① ② ③ 中,①和②是方程 的解;是方程 的解;不解方程组,可写出方程组 的解为 .
16. 在① ② ③ 中,①和②是方程 的解;是方程 的解;不解方程组,可写出方程组 的解为 .三、解答题
-
17. 判断下列方程组是否为二元一次方程组,并说明理由.
⑴
⑵
⑶
⑷
⑸ .
18. 根据下列语句,分别设适当的未知数,列出二元一次方程或方程组:(1)、甲数的 比乙数的2倍少7;(2)、摩托车的时速是货车的 倍,它们的速度之和是150.19. 根据题意列出方程组:(1)、明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,问明明两种邮票各买了多少枚?(2)、将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?20. 根据题意设未知数,并列出方程组:(1)、某校七年级二班组织全班同学共40人去参加义务植树活动,男生每人植树4棵,女生每人植树3棵,全组共植树123棵.求男生和女生各有多少人?(2)、某人从学校出发骑自行车去县城,中途因为道路施工步行一段路,1.5小时后到达县城.他骑车的平均速度是15千米/时,步行的平均速度是5千米/时,路程全长20千米,他骑车与步行各用多少时间?(3)、加工某种产品需要两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件,现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一、第二道工序所完成的件数相等?.