2021-2022学年浙教版数学七下1.3平行线的判定同步练习

试卷更新日期：2022-01-28 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，直线 a ， b 被直线 c ， d 所截下列条件能判定 a//b 的是（   ）

    A、∠1=∠3 B、∠2+∠4=180∘ C、∠4=∠5 D、∠1=∠2

    查看试题解析

  • 2. 如图，下列条件中①∠1＝∠2； ②∠3＝∠4； ③∠2＋∠5＝∠6 ；④∠DAB＋∠2＋∠3＝180°，能判断AD∥BC的是（  ）

    A、①③④ B、①②④ C、①③ D、①②③④

    查看试题解析

  • 3. 下列图形中，由∠1＝∠2，能得到AB∥CD的是（   ）.
    A、 B、 C、 D、

    查看试题解析

  • 4. 如图，图中给出了过直线外一点作已知直线的平行线的方法，其依据的是（   ）

    A、同位角相等，两直线平行 B、同旁内角互补，两直线平行 C、内错角相等，两直线平行 D、同平行于一条直线的两直线平行

    查看试题解析

  • 5.

    如图，下列条件中能判定直线l1∥l2的是（    ）

    A、∠1=∠2 B、∠1=∠5 C、∠1+∠3=180° D、∠3=∠5

    查看试题解析

  • 6. 如图，直线AC、DC、BE相交于点C，连接AB，能判定AB∥CD的条件是（   ）

    A、∠A=∠ACB B、∠B=∠ACD C、∠B+∠DCE=180° D、∠A=∠ACD

    查看试题解析

  • 7. 给出下列说法：
    （1）两条直线被第三条直线所截，同位角相等.（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交.（3）相等的两个角是对顶角.（4）从直线外一点到这条直线的垂线段，叫做这点到直线的距离.其中正确的有（   ）.
    A、0个 B、1个 C、2个 D、3个

    查看试题解析

  • 8. 如图， ∠AEF=∠EFC ，则下列结论中正确的是（   ）

    A、EF//BC B、AD//BC C、AD//EF D、AB//CD

    查看试题解析

  • 9. 如图，给出下列条件：① ∠CAD=∠ACB ；② ∠CAB=∠ACD ；③ AD//BE 且 ∠D=∠B ；其中能推出 AB//DC 的条件个数是（   ）

    A、0个 B、1个 C、2个 D、3个

    查看试题解析

  • 10. 如图，由两个完全相同的三角板拼成一个四边形，则下列条件能直接判断 AD//BC 的是（   ）

    A、∠ADB=∠CBD B、∠ABD=∠CDB C、∠BAD=∠DCB D、∠BAD+∠CDA=180°

    查看试题解析

二、填空题

  • 11. “过点P作直线b，使b∥a"，小明的作图痕迹如图所示，他的作法的依据是

    查看试题解析

  • 12. 如图，直线a，b被直线c所截，当∠1 ∠2时，a//b.（用“＞”，“＜”或“＝”填空）

    查看试题解析

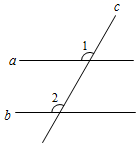  • 13. 将一副三角板如图摆放，则∥ ， 理由是.

    查看试题解析

  • 14. 如图，不添加辅助线，请添加一个能判定 DE//BC 的条件： ．

    查看试题解析

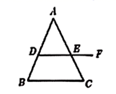  • 15. 如图，点E在AC的延长线上，对于给出的四个条件：（1）∠3=∠4；（2）∠1=∠2；（3）∠A=∠DCE；（4）∠D+∠ABD=180°.能判断AB∥CD的有个.

    查看试题解析

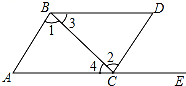  • 16. 如图，∠A＝70°，O是AB上一点，直线OD与AB的夹角∠BOD为75°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转度.

    查看试题解析

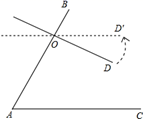  • 17. 如图，要使AD//BF，则需要添加的条件是（写一个即可）.

    查看试题解析

  • 18. 如图，在三角形ABC中，点D ， E分别在边AC ， BC上，请你添加一个条件 ， 使得DE // AB ． （要求：不再添加辅助线，只需填一个答案即可）

    查看试题解析

三、综合题

  • 19. 小明在学习三角形的知识时，发现如下数学问题：

    已知线段AB，CD交于点E，连结AD，BC．

    (1)、如图①，若∠D＝∠B＝100°，∠DAB的平分线与∠BCE的平分线交于点G，求∠G的度数；
    (2)、如图②，若∠D＝∠B＝90°，AM平分∠DAB，CF平分∠BCN，请判断CF与AM的位置关系，并说明理由．

    查看试题解析

  • 20. （问题情境）：如图 AB // CD ， ∠PAB=120∘ ， ∠PCD=140∘ ，求 ∠APC 的度数.

    小明的思路是：过 P 作 PE // AB ，通过平行线性质来求 ∠APC .

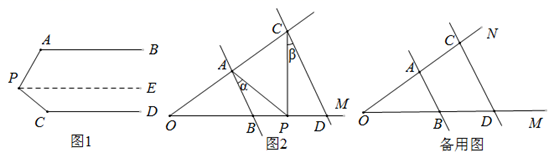    (1)、按小明的思路，求 ∠APC 的度数；
    (2)、（问题迁移）：如图2，AB//CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
    (3)、（问题应用）：在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系.

    查看试题解析

  • 21. 下面是嘉琪同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程．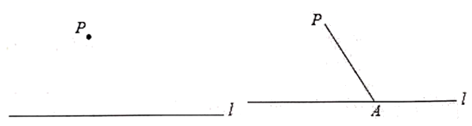

    已知：如图，直线l和直线l外一点P ．

    求作：直线PQ ， 使直线PQ // 直线l ．

    作法：如图，

    ①在直线l上取一点A ， 连接PA；

    ②作PA的垂直平分线MN ， 分别交直线l ， 线段PA于点B ， O；

    ③以O为圆心，OB长为半径作弧，交直线MN于另一点Q；

    ④作直线PQ ， 所以直线PQ为所求作的直线．

    根据上述作图过程，回答问题：

    (1)、用直尺和圆规，补全图中的图形（保留作图痕迹）；
    (2)、完成下面的证明：

    证明：∵直线MN是PA的垂直平分线，

    ∴  ▲  ＝  ▲  ， ∠POQ＝∠AOB＝90°．

    ∴△POQ≌△AOB ．

    ∴   ▲  ＝   ▲   ，

    ∴PQ // l（  ▲  ）（填推理的依据）．

    查看试题解析

  • 22. 如图，射线 BC 平外 ∠ABD ，且 ∠1+∠2=180° .求证： AB//CD .

    查看试题解析

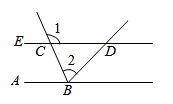  • 23. 如图，AC//EF，∠1+∠3=180º．

    (1)、AF与CD是否平行？请说明理由；
    (2)、若AC平分∠FAB，AC⊥EB于点C，∠4=78º，求∠BCD的度数．

    查看试题解析

  • 24. 如图，已知点E在直线DC上，射线EF平分 ∠AED ，过E点作 EB⊥EF ，G为射线EC上一点，连接BG，且 ∠EBG+∠BEG=90° .

    (1)、求证： ∠DEF=∠EBG ；
    (2)、若 ∠EBG=∠A ，求证： AB//EF .

    查看试题解析

  • 25. 【学科融合】

    物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）.由此可以归纳出如下的规律：

    在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角.这就是光的反射定律（rfectionlaw）.

    【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD.由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4.在这样的条件下，求证：AB∥CD.

    【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD.

    (1)、如图2，光线AB与CD相交于点E，则∠BEC＝；
    (2)、如图3，光线AB与CD所在的直线相交于点E，CBED＝β，则α与β之间满足的等量关系是.

    查看试题解析