浙江省舟山市临城区域2021-2022学年九年级上学期数学期末考试试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分.）

1. 下列事件中，属于必然事件的是（）

A、任意抛掷一只纸杯，杯口朝下 B、a为实数，｜a｜＜0 C、打开电视，正在播放动画片 D、任选三角形的两边，其差小于第三边

查看试题解析
2. 已知圆内接四边形 $A B C D$ 中， $∠ A : ∠ C = 1 : 2$ ，则 $∠ A =$ （）

A、 $50^{°}$ B、 $60^{°}$ C、 $100^{°}$ D、 $\begin{array}{l} 120^{°} \end{array}$

查看试题解析
3. 抛物线y＝2x²＋1的对称轴是（）

A、直线 $x = \frac{1}{2}$ B、直线 $x = - \frac{1}{2}$ C、直线 $x = 2$ D、y轴

查看试题解析
4. 已知一个正多边形的内角是140°，则它是几边形（）

A、10 B、9 C、8 D、7

查看试题解析
5. 在平面直角坐标系中，点P的坐标为（3，m），若OP与y轴相切，那么⨀P与直线x＝5的位置关系是（）

A、相交 B、相切 C、相离 D、不能确定

查看试题解析
6. 在直角ΔABC中，已知∠C＝90°， $sinA = \frac{1}{3}$ ，求cosA=（）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $2 \sqrt{2}$

查看试题解析
7. 如图，在直角坐标系中，点A在第一象限内，点B在x轴正半轴上，以点O为位似中心，在第三象限内与ΔOAB的位似比为 $\frac{1}{3}$ 的位似图形ΔOCD.若点C的坐标为 $(- 1 ， - \frac{2}{3})$ ，则点A的坐标为（）

A、 $(\frac{2}{3} ， 2)$ B、 $（ \frac{2}{3} ， 2 ）$ C、 $(3 ， \frac{2}{3})$ D、 $(3 ， 2)$

查看试题解析
8. 某品牌汽车将汽车倒车镜设计为整个车身黄金分割点的位置（如图），若车头与倒车镜的水平距离为1.58米，倒车镜到车尾部分的水平距离较长，则该车车身总长约为（）米.

A、4.14 B、2.56 C、6.70 D、3.82

查看试题解析
9. 如图，明年舟山将再添一个最高颜值城市新地标，新城长峙岛上将矗立起一座摩天轮，其直径为90m，旋转1周用时15min．小明从摩天轮的底部（与地面相距0.5m）出发开始观光，摩天轮转动1周，小明在离地面68m以上的空中有多长时间？（）

A、3min B、5min C、6min D、10min

查看试题解析
10. 点P（x₁ ， y₁），Q（x₂ ， y₂）在抛物线y＝ax²-4ax＋2（a＞0）上，若对于t＜x₁＜t＋1，t＋2＜x₂＜t＋3，都有y₁≠y₂ ，则t的取值范围是（）

A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-1

查看试题解析

二、填空题（本题有6小题，每题4分，共24分）

11. 若 $3 x = 2 y$ ，则 $\frac{x}{y} =$ .

查看试题解析
12. 将抛物线 $y = x^{2}$ 向上平移3个单位，所得图象的函数表达式是。

查看试题解析

13. 十一国庆期间，小明爸爸从金塘收费站出发到舟山市人民政府办事，导航显示有两条路径可以选择，L₁：经过东西快速路；L₂：经过海天大道。据统计，通过两条路径所用的时间互不影响所用时间，所用时间落在各时间段内的频率如下表：（由公路部门根据当天统计）小明爸爸只有55分钟时间用于赶往目的地，请问他会选择路径．（填L₁或L₂）

时间（分）	35~40	40~50	45~50	50~55	55~60
L₁的频率	0.1	0.2	0.2	0.3	0.2
L₂的频率	0	0.1	0.5	0.3	0.1

查看试题解析

14. 如图，在ΔABC中，∠ACB＝90°，D是BC边上的点，CD＝2，以CD为直径的⨀O与AB相切于点E.若弧DE的长为 $\frac{π}{3}$ 则阴影部分的面积.（保留π）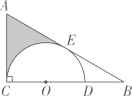

查看试题解析
15. 如图，在ΔABC中，BC＝20，点B₁ ， B₂ ， B₃ ， B₄和点C₁ ， C₂ ， C₃ ， C₄分别是AB，AC的5等分点，则B₁C₁＋B₂C₂＋B₃C₃＋B₄C₄的值为。

查看试题解析
16. 如图，在直角∆ABC中，∠C＝90°，AC＝8，BC＝6，点M从点C出发沿线段CA向点A移动，连接BM，MN⟂BM交边AB于点N．若CM＝2，那么线段AN＝；当点M从点C移动到AC的中点时，则点N的运动过程中路径长为。

查看试题解析

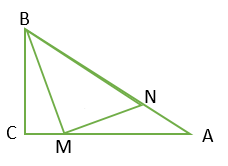
三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17. 计算

(1)、2sin30°＋tan45°

(2)、 $\frac{1}{1 + 2cos45 °}$

查看试题解析
18. 现有三位“抗疫”英雄（依次标记为A，B，C）．为了让同学们了解他们的英雄事迹，张老师设计了如下活动：取三张完全相同的卡片，分别在正面写上A，B，C三个标号，然后背面朝上放置，搅匀后请一位同学从中随机抽取一张，记下标号后放回，要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.

(1)、求班长在这三种卡片中随机抽到标号为C的概率；

(2)、用树状图或列表法求小明和小亮两位同学抽到的卡片是不同“抗疫”英雄标号的概率.

查看试题解析
19. 近几年中学生近视的现象越来越严重，为响应国家的号召，某公司推出了如图1所示的护眼灯，其侧面示意图（台灯底座高度忽略不计）如图2所示，其中灯柱BC＝18cm，灯臂CD＝33cm，灯罩DE＝20cm，BC⊥AB，CD、DE分别可以绕点C、D上下调节一定的角度．经使用发现：当∠DCB＝140°，且ED∥AB时，台灯光线最佳．求此时点D到桌面AB的距离．（精确到0.1cm，参考数值：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

查看试题解析
20. 在6x6的正方形网格中，每个小正方形的顶点称为格点，请你借助格点，仅用无刻度的直尺按要求作图.（保留作图痕迹）

(1)、如图1，线段AB的端点A，B均在格点上，作出线段AB的中点P；

(2)、如图2，线段CD的端点C，D均在格点上，作出线段CD的三等分点．

查看试题解析
21. 某公司今年国庆期间在网络平台上进行直播销售猕猴桃，已知猕猴桃的成本价格为8元／kg，经销售发现：每日销售量y（kg）与销售单价x（元／kg）满足一次函数关系，下表记录的是有关数据，销售单价不低于成本价且不高于24元／kg．设公司销售猕猴桃的日获利为w（元）.

x（元／kg）

9

10

11

y(kg)

2100

2000

1900

(1)、请求出日销售量y与销售单价x之间的函数关系式；

(2)、当销售单价定为多少时，销售这种猕猴桃日获利w最大？最大利润为多少元？

查看试题解析
22. 已知：如图1，AB是OO的直径，点C，E都在OO上，OC⊥AB， $\overset{⌢}{E C} = 2 \overset{⌢}{E A}$ ，DE∥AB交OC于点D．

(1)、求证：点D是线段CO的中点；

(2)、延长OC至点F，使FC＝OC，连接EF，判断EF与⨀O的位置关系，并说明理由.

查看试题解析
23. 如图，二次函数y＝x2＋bx＋c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x＝1对称，点A的坐标为（-1，0）．

(1)、求二次函数的表达式；

(2)、当y＜0时，写出x的取值范围；

(3)、当a≤x≤a＋1时，二次函数y＝x²＋bx＋c的最小值为2a，求a的值．

查看试题解析
24. 如图，ΔDBE内接于⊙O，BD为直径，DE＝EB，点C在⊙O（不与D，B，E重合）上，∠A＝45°，点A在直线CD上，连接AB．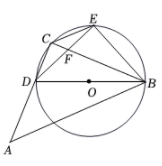

(1)、如图1，若点C在DE上，求证：ΔABD～ΔCBE；

(2)、在（1）的条件下，DC＝6，DB＝10，求线段CE的长；

(3)、若直线BC与直线DE相交于点F，当 $\frac{D C}{C B} = \frac{1}{3}$ 时，求 $\frac{B F}{D F}$ 的值。

查看试题解析

x（元／kg）	9	10	11
y(kg)	2100	2000	1900