浙江省宁波市海曙区2021--2022学年九年级上学期数学期末试卷
试卷更新日期:2022-01-27 类型:期末考试
一、选择题(每小题4分,共 40 分)
-
1. 台球盒中有7个红球与1个黑球, 从中随机摸出一个台球, 则下列描述符合的是( )A、一定摸到黑球 B、不可能摸到黑球 C、很可能摸到黑球 D、不大可能摸到黑球2. 已知抛物线 , 其对称轴是( )A、直线 B、直线 C、直线 D、直线3. 如图 中, 分别在边 上, , 则 ( )
 A、6 B、12 C、18 D、244. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( )
A、6 B、12 C、18 D、244. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( ) A、 米 B、 米 C、 米 D、 米5. 如图, 是 的直径, 是弦, , 则 的度数是( )
A、 米 B、 米 C、 米 D、 米5. 如图, 是 的直径, 是弦, , 则 的度数是( )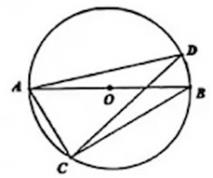 A、 B、 C、 D、6. 如图, 在 中, , 以点 为旋转中心, 将 绕点 逆时针旋转得到 , 点 的对应点分别为 , 连接 , 若 , 则 的值是( )
A、 B、 C、 D、6. 如图, 在 中, , 以点 为旋转中心, 将 绕点 逆时针旋转得到 , 点 的对应点分别为 , 连接 , 若 , 则 的值是( ) A、 B、 C、 D、7. 如图, 在圆形方格网横线上, 点 是直径 与网格横线的交点, 则 为( )
A、 B、 C、 D、7. 如图, 在圆形方格网横线上, 点 是直径 与网格横线的交点, 则 为( ) A、 B、 C、 D、8. 若二次函数 的图象如图所示,则下列说法不正确的是( )
A、 B、 C、 D、8. 若二次函数 的图象如图所示,则下列说法不正确的是( ) A、当 时, B、当 时, 有最大值 C、图像经过点 D、当 时,9. 如图,将5个全等的等腰三角形拼成内外两个大小不同的正五边形图案,设小正五边形边长为1,则大正五边形边长为( )
A、当 时, B、当 时, 有最大值 C、图像经过点 D、当 时,9. 如图,将5个全等的等腰三角形拼成内外两个大小不同的正五边形图案,设小正五边形边长为1,则大正五边形边长为( ) A、 B、 C、 D、10. 如图, 四边形 中, , 以 为直径的 刚好与 相切, 连结 交于点 , 若 , 则已知下列条件中的一个即可求 的长的有( )
A、 B、 C、 D、10. 如图, 四边形 中, , 以 为直径的 刚好与 相切, 连结 交于点 , 若 , 则已知下列条件中的一个即可求 的长的有( )

(1) ;(2) ; (3) ; (4) .A、(1)、(2)、(3)、(4) B、(1)、(2)、(3) C、(1)、(2)、(4) D、(1)、(3)、(4)二、填空题 (每小题5分, 共30分)
-
11. 若 , 则 .12. 小明随意抛掷一枚点数从 , 质地均匀的正方体骰子, 前面8次中有5次3点朝上. 则执第9次时, 3点朝上的概率为.13. 如图, 将直径 的半圆 , 绕端点 逆时针旋转, 当圆弧与直径交点 满足 时, 的值为.
 14. 在芯片制作过程中, 需要对 的矩形区域进行划区处理, 划成如图所示的“ ” 的形式, 其中 为竖式矩形 为横式矩形 , 则芯片被利用区域的长 的值为 cm .
14. 在芯片制作过程中, 需要对 的矩形区域进行划区处理, 划成如图所示的“ ” 的形式, 其中 为竖式矩形 为横式矩形 , 则芯片被利用区域的长 的值为 cm .
 15. 如图,已知距离为6的两条平行线 与 分别交于 两点 为直径,且与 不垂直), D为 上一点, 过 作 的平行线 交 于点 , 若 , 则 的长为 .
15. 如图,已知距离为6的两条平行线 与 分别交于 两点 为直径,且与 不垂直), D为 上一点, 过 作 的平行线 交 于点 , 若 , 则 的长为 . 16. 如图, 抛物线 与 轴交于点 和点 两点, 与 轴交于点 点为拋物线上第三象限内一动点, 当 时, 点 的坐标为 .
16. 如图, 抛物线 与 轴交于点 和点 两点, 与 轴交于点 点为拋物线上第三象限内一动点, 当 时, 点 的坐标为 .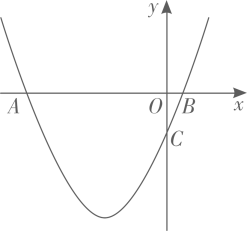
三、解答题(第17 题 6 分,18 题8分,第 题每题10分, 第23题12分, 第24 题14 分, 共80分)
-
17. 计算:18. 在一个不透明的口袋里装有分别标注 1、2 的两个小球 (小球除数字外, 其余都相同), 另有背面完全一样、正面分别写有 3、4、5 的三张卡片, 现从口袋中任意摸出一个小球, 再从这三张背面朝上的卡片中任意摸出一张, 则(1)、共有多少种结果? (请用列表或者画树状图的方法表示说明)(2)、小方和小圆选择下列两个规则中的一个做游戏:
①若两次摸出的数字, 和为奇数, 则小方赢, 否则小圆赢;
②若两次摸出的数字, 积为奇数, 则小方赢, 否则小圆赢。
小方想要在游戏中获胜机会更大些, 他应选择哪一条规则, 请说明理由.
19. 如图, 在 的正方形方格纸中, 的顶点在格点上,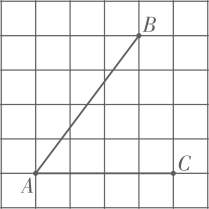 (1)、直接写出 .(2)、仅用直尺, 画出 的平分线 , 并写出 .20. 定义: 若抛物线 与地物线 . 同时满足 且 , 则称这两条抛物线是一对 “共轭抛物线".
(1)、直接写出 .(2)、仅用直尺, 画出 的平分线 , 并写出 .20. 定义: 若抛物线 与地物线 . 同时满足 且 , 则称这两条抛物线是一对 “共轭抛物线". (1)、已知抛物线 与 是一对共轭抛物线, 求 的解折式:(2)、如图1,将一副边长为 的正方形七巧板拼成图2的形式, 若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点 的抛物线为 , 经过 的抛物线为 , 请立接写出 的解析式并判断它们是否为一对共轭拋物线.21. 如图, 扇形圆心角 , 半径 , 把扇形做成圆锥后, 其底面半径为2 ,
(1)、已知抛物线 与 是一对共轭抛物线, 求 的解折式:(2)、如图1,将一副边长为 的正方形七巧板拼成图2的形式, 若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点 的抛物线为 , 经过 的抛物线为 , 请立接写出 的解析式并判断它们是否为一对共轭拋物线.21. 如图, 扇形圆心角 , 半径 , 把扇形做成圆锥后, 其底面半径为2 , (1)、求 :(2)、点 是 上的一点, 若 , 求 .22. 如图,已知AB是半圆O的直径,C是半圆弧上一点,P是BC的中点,PD//BC交AB延长线于点D.
(1)、求 :(2)、点 是 上的一点, 若 , 求 .22. 如图,已知AB是半圆O的直径,C是半圆弧上一点,P是BC的中点,PD//BC交AB延长线于点D.求证:
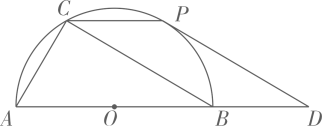 (1)、 为 的切线;(2)、若 , 的值.23. 如图, 在平面直角坐标系中, 过点 两点的拋物线的顶点 在 轴正半轴上,
(1)、 为 的切线;(2)、若 , 的值.23. 如图, 在平面直角坐标系中, 过点 两点的拋物线的顶点 在 轴正半轴上, (1)、求抛物线的解析式;(2)、求点 的坐标;(3)、 为线段 上一点, , 作 轴交抛物线于点 , 求PM的最大值与最小值.24. 如图
(1)、求抛物线的解析式;(2)、求点 的坐标;(3)、 为线段 上一点, , 作 轴交抛物线于点 , 求PM的最大值与最小值.24. 如图 (1)、如图1,在正方形ABCD中,点E是AD边上一点,点P为BC边上一点,PE交AC于点F,已知 , 设 ,
(1)、如图1,在正方形ABCD中,点E是AD边上一点,点P为BC边上一点,PE交AC于点F,已知 , 设 ,请直接写出 ∠PEC= , ∠EPC= , PC= (用 或m相关的代数式表示)
(2)、作 分别交 于 (如图2),求 的长;(3)、连结 , 若 , 求 的最小值;(4)、在(3)的条件下,请直接写出 的最小值时, = ,