浙江省宁波市海曙区2021-2022学年八年级上学期数学期末考试试卷
试卷更新日期:2022-01-27 类型:期末考试
一、单选题(共10题,满分30分,每小题3分)
-
1. 下面图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组数中,不可能成为一个三角形三边长的是( )
2. 下列各组数中,不可能成为一个三角形三边长的是( )
A、2,3,4 B、5,7,7 C、5,6,12 D、6,8,103. 若 成立,则下列不等式不成立的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点 与点 关于 轴对称,则( )A、 , B、 , C、 , D、 ,5. 下列命题是真命题的是( )A、等腰三角形的顶角一定是锐角 B、三个角对应相等的两个三角形全等 C、每个定理都有逆定理 D、等腰三角形的底角小于 90°6. 如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( ) A、4 B、6 C、8 D、127. 点 在函数 的图像上,则代数式 的值等于( )A、5 B、-3 C、3 D、-18. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
A、4 B、6 C、8 D、127. 点 在函数 的图像上,则代数式 的值等于( )A、5 B、-3 C、3 D、-18. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、 B、
B、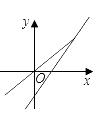 C、
C、 D、
D、 9. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
9. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
 A、1 B、2 C、3 D、410. 如图,在 中, , , 为 边的中点, , 绕 点旋转,它的两边分别交 和 的延长线于 , ,当点 在 延长线上时, , , 的关系为( )
A、1 B、2 C、3 D、410. 如图,在 中, , , 为 边的中点, , 绕 点旋转,它的两边分别交 和 的延长线于 , ,当点 在 延长线上时, , , 的关系为( ) A、 = B、 = C、 = D、 =
A、 = B、 = C、 = D、 =二、填空题(共8小题,满分32分,每小题4分)
-
11. 在 中, , ,则 是三角形.(选填“锐角”、“直角”或“钝角”)12. 如图,在 中, , ,点 在 的延长线上,则 等于 .
 13. 不等式2x﹣1≤6的非负整数解有个.14. 在平面直角坐标系中,直线 和直线 的交点的横坐标为 .若 ,则实数 的取值范围为.15. 一艘轮船从海平面上A地出发,向北偏东50°的方向行驶60海里到达B地,再由B地向南偏东10°的方向行驶60海里到达C地,则A,C两地相距 海里.16. 已知 y是关于x的一次函数,下表列出了部分对应值,则a的值为 .
13. 不等式2x﹣1≤6的非负整数解有个.14. 在平面直角坐标系中,直线 和直线 的交点的横坐标为 .若 ,则实数 的取值范围为.15. 一艘轮船从海平面上A地出发,向北偏东50°的方向行驶60海里到达B地,再由B地向南偏东10°的方向行驶60海里到达C地,则A,C两地相距 海里.16. 已知 y是关于x的一次函数,下表列出了部分对应值,则a的值为 .x 1 2 3 y 3 a 5 17. 已知四边形 , , , ,如果 ,则 的长为.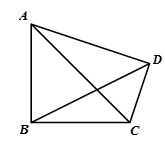 18. 在平面直角坐标系中,Q是直线 上的一个动点,将Q绕点 顺时针旋转 ,得到点 连接 ,则 的最小值为 .
18. 在平面直角坐标系中,Q是直线 上的一个动点,将Q绕点 顺时针旋转 ,得到点 连接 ,则 的最小值为 .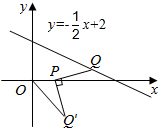
三、解答题(共6小题,满分58分,19-20每题8分,21-23每题10分,24题12分)
-
19. 解下列不等式 (组):(1)、4x-1≥2x+4(2)、20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).

⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶写出点B′的坐标.
21. 已知y是x的一次函数,且当 时, ;当 时, .(1)、求这个一次函数的解析式;(2)、当 时,求函数y的值;(3)、当 时,求自变量x的取值范围.22. 如图,在 中, , ,F为 延长线上一点,点E在 上,且 .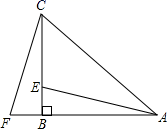 (1)、求证: ;(2)、若 ,求 的度数.23. 我省要按照城市功能特点,城区消费到2022年,建设20个省内特色消费中心,着力发展“夜经济”,打造郑州“夜商都”等地方夜消费品牌升级版.允许市场经营主体在规范有序的条件下,采取“店铺外摆”“露天市场”方式进行销售.个体业主小王响应号召,采取“店铺外摆”方式销售甲、乙两款特价商品,两款商品的进价与售价如表所示:
(1)、求证: ;(2)、若 ,求 的度数.23. 我省要按照城市功能特点,城区消费到2022年,建设20个省内特色消费中心,着力发展“夜经济”,打造郑州“夜商都”等地方夜消费品牌升级版.允许市场经营主体在规范有序的条件下,采取“店铺外摆”“露天市场”方式进行销售.个体业主小王响应号召,采取“店铺外摆”方式销售甲、乙两款特价商品,两款商品的进价与售价如表所示:甲商品
乙商品
进价(元/件)
35
5
售价(元/件)
45
8
小王计划购进甲、乙两种商品共100件进行销售.设小王购进甲商品 件,甲、乙商品全部销售完后获得的利润为 元.
(1)、求出 与 之间的函数关系式;(2)、若购进乙商品的件数不少于甲商品件数的3倍,当购进甲,乙两种商品各多少件时,可使得甲、乙商品全部销售完后获得的利润最大?24. 如图所示, 中, , 于点 , , .
 (1)、求 , 的长.(2)、若点 是射线 上的一个动点,作 于点 ,连结 .
(1)、求 , 的长.(2)、若点 是射线 上的一个动点,作 于点 ,连结 .①当点 在线段 上时,若 是以 为腰的等腰三角形,请求出所有符合条件的 的长.
②设 交直线 于点 ,连结 , ,若 ,则 的长为多少?(直接写出结果).