四川省南充市2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、单选题

1. 出行安全，认识交通路标非常重要.下列是部分交通路标，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. ${(- a^{3})}^{2}$ 的值是（）

A、 $- a^{5}$ B、 $a^{6}$ C、 $a^{5}$ D、 $- a^{6}$

查看试题解析
3. 已知三角形的两边长分别为2cm和3cm，则第三边长可能是（）

A、6cm B、5cm C、3cm D、1cm

查看试题解析
4. 计算 $m (m + 1) (m + 2)$ 结果中， $m^{3}$ 项的系数是（）

A、0 B、1 C、2 D、3

查看试题解析
5. 如图， $△ A D E ≌ △ B C F$ ， $A D = 10$ cm， $C D = 6$ cm，则 $B D$ 的长为（）

A、4cm B、3cm C、2cm D、不能确定

查看试题解析
6. 如果分式 $\frac{m^{2} - 4}{m - 2}$ 的值为零，那么 $m$ 的值是（）

A、 $m \neq 2$ B、 $m = \pm 2$ C、 $m = - 2$ D、 $m = 2$

查看试题解析
7. 一副三角板按如图所示叠放在一起，则图中∠α的度数是（）

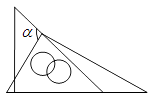A、60° B、75° C、90° D、105°

查看试题解析
8. 若代数式 $\frac{x^{2}}{x - 1} ◯ \frac{x}{x - 1} (x \neq 0)$ 运算结果为x，则在“○”处的运算符号应该是（）

A、除号“÷” B、除号“÷”或减号“-” C、减号“-” D、乘号“×”或减号“-”

查看试题解析
9. 如图，点B，C，E在同一直线上，且 $A C = C E$ ， $∠ B = ∠ D = 90 °$ ， $A C ⊥ C D$ ，下列结论不一定成立的是（）

A、 $∠ A = ∠ 2$ B、 $∠ A + ∠ E = 90 °$ C、 $B C = D E$ D、 $∠ B C D = ∠ A C E$

查看试题解析
10. 设 $M = (1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \cdot \cdot \cdot (1 - \frac{1}{n^{2}})$ （ $n \geq 2$ 的自然数），如果 $\frac{6}{M}$ 是整数，n的值有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 计算 $2^{- 2}$ 的结果是．

查看试题解析
12. 如图， $△ A B C$ 与 $△ D C B$ 中，已知， $∠ A = ∠ D$ ，请你添加一个条件（不添加字母和辅助线），使 $△ A B C ≌ △ D C B$ ，你添加的条件是.

查看试题解析
13. 已知 $a^{2} - b^{2} = 8$ ， $a - b = 4$ ，则 $a + b =$ .

查看试题解析
14. 若一个多边形的一条对角线把它分成两个四边形，则这个多边形的内角和是度.

查看试题解析
15. 已知 $x - \frac{1}{x} = 4$ ，则 $x^{2} + \frac{1}{x^{2}} =$ .

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A C B = 30 °$ ， $A B = 4$ ，高 $C H = 6$ .作点H关于 $A C$ ， $B C$ 的对称点D，E，连接 $D E$ 交 $A C$ 于点P，交 $B C$ 于点Q；连接 $H D$ ， $H P$ ， $H Q$ ， $H E$ .下列结论：① $∠ D C E = 60 °$ ；② $P Q = 3$ ；③五边形 $A B E C D$ 的面积是24；④ $△ P Q H$ 的周长为6.其中正确结论是.（填写序号）

查看试题解析

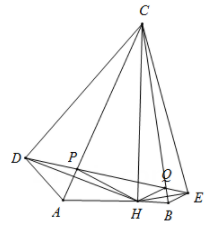
三、解答题

17. 计算：

(1)、 $(12 a^{3} b - 3 a) \div 3 a$ ；

(2)、 $(a - b) (a + 2 b) - {(a + b)}^{2}$ .

查看试题解析
18. 如图， $A D$ 是 $△ A B C$ 的中线，F为 $A D$ 上一点，E为 $A D$ 延长线上一点，且 $D F = D E$ .求证： $B E ∥ C F$ .

查看试题解析
19. 先化简，再求值： $\frac{2 x^{2} - x}{x^{2} - 2 x + 1} \div \frac{2 x - 1}{x - 1} - 1$ ，其中 $x = 3$ .

查看试题解析
20. 分解因式：

(1)、 $4 m^{3} - 8 m^{2} + 4 m$ ；

(2)、 $a^{2} (a - b) + (b - a)$ .

查看试题解析
21. 如图，在 $△ A B C$ 中， $C D$ 为 $△ A B C$ 的高， $A E$ 为 $△ A B C$ 的角平分线， $C D$ 交 $A E$ 于点G， $∠ B C D = 50 °$ ， $∠ B E A = 110 °$ ，求 $∠ A C D$ 的大小.

查看试题解析
22. 如图，在平面直角坐标系xOy中有一个 $△ A B C$ ，其中点 $A (- 2 ， 3)$ .

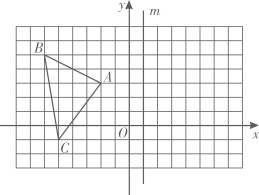(1)、若 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 关于x轴对称，直接写出 $△ A_{1} B_{1} C_{1}$ 三个顶点的坐标；

(2)、作 $△ A B C$ 关于直线m的对称图形 $△ A_{2} B_{2} C_{2}$ ，并写出 $B_{2}$ 和 $C_{2}$ 的坐标.

查看试题解析
23. 新型冠状病毒肺炎疫情发生后，全社会积极参与疫情防控.某呼吸机厂接到生产600台呼吸机的任务，以每天比原来多生产50台呼吸机的速度进行生产，结果所用时间与原来生产450台呼吸机所用时间相同.

(1)、求该厂现在每天生产多少台呼吸机?

(2)、完成这批任务后，该厂又接到在10天内至少生产2400台呼吸机的任务，问该厂每天还应该至少比现在多生产多少台呼吸机才能完成任务?

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是 $A B$ 边的高.将 $A C$ 边对折，折痕为 $E F$ ，连接 $C E$ ， $C D$ 平分 $∠ B C E$ .

(1)、求 $∠ A$ 的度数.

(2)、连接 $D F$ ，求证： $A F = D F$ .

查看试题解析
25.

(1)、阅读理解：问题：如图1，在四边形 $A B C D$ 中，对角线 $B D$ 平分 $∠ A B C$ ， $∠ A + ∠ C = 180 °$ .求证： $D A = D C$ .
思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.

方法1：在 $B C$ 上截取 $B M = B A$ ，连接 $D M$ ，得到全等三角形，进而解决问题；

方法2：延长 $B A$ 到点N，使得 $B N = B C$ ，连接 $D N$ ，得到全等三角形，进而解决问题.

结合图1，在方法1和方法2中任选一种，添加辅助线并完成证明.

(2)、问题解决：如图2，在（1）的条件下，连接 $A C$ ，当 $∠ D A C = 60 °$ 时，探究线段 $A B$ ， $B C$ ， $B D$ 之间的数量关系，并说明理由；

(3)、问题拓展：如图3，在四边形 $A B C D$ 中， $∠ A + ∠ C = 180 °$ ， $D A = D C$ ，过点D作 $D E ⊥ B C$ ，垂足为点E，请直接写出线段 $A B$ 、 $C E$ 、 $B C$ 之间的数量关系.

查看试题解析