陕西省宝鸡市凤翔区2021-2022学年八年级上学期期末考试数学试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、单选题

1. 实数﹣3，3，0， $\sqrt{2}$ 中最大的数是（　　）

A、﹣3 B、3 C、0 D、 $\sqrt{2}$

查看试题解析
2. 下列说法正确的是（）

A、过直线上一点有且只有一条直线与已知直线平行 B、不相交的两条直线叫做平行线 C、直线外一点到该直线的所有线段中垂线最短 D、过直线外一点有且只有一条直线与已知直线平行

查看试题解析
3. 小雨同学参加了学校举办的“抗击疫情，你我同行”主题演讲比赛，她的演讲内容语言表达和形象风度三项得分分别为80分，90分，85分，若这三项依次按照50%，30%，20%的百分比确定成绩，则她的成绩是（）

A、82分 B、83分 C、84分 D、85分

查看试题解析
4. 若点 $P (m ， n)$ 在第三象限，则点 $Q (- m ， - n)$ 在（）.

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 由2x+3y﹣6＝0可以得到用x表示y的式子为（　　）

A、 $y = - \frac{2}{3} x - 2$ B、 $y = \frac{2}{3} x - 2$ C、 $y = \frac{2}{3} x + 2$ D、 $y = - \frac{2}{3} x + 2$

查看试题解析
6. 一次函数y＝kx－k(k＜0)的图象大致是（）

A、 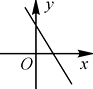B、 C、 D、

查看试题解析
7. 如图，以 $R t △ A B C$ 的三边为直角边分别向外作等腰直角三角形.若 $A B = \sqrt{3}$ ，则图中阴影部分的面积为（　　）

A、3 B、 $\frac{9}{2}$ C、 $3 \sqrt{2}$ D、 $3 \sqrt{5}$

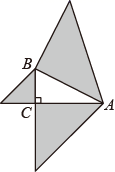查看试题解析
8. 学习平行线后，张明想出了过已知直线外一点画这条直线的平行线的新方法，他是通过折一张半透明的纸得到的．观察图（1）～（4），经两次折叠展开后折痕CD所在的直线即为过点P与已知直线a平行的直线．由操作过程可知张明画平行线的依据有（）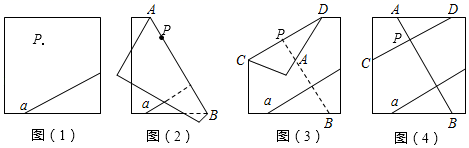

①同位角相等，两直线平行；

②两直线平行，同位角相等；

③内错角相等，两直线平行；

④同旁内角互补，两直线平行．

A、①③ B、①②③ C、③④ D、①③④

查看试题解析

二、填空题

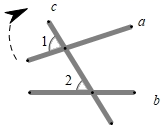
9. 一次函数 $y = - 3 x + 4$ 的图象与x轴的交点坐标为.

查看试题解析
10. 直角三角形的两条边长分别为3cm、4cm，则这个直角三角形的斜边长为cm.

查看试题解析
11. 小刘和小李参加射击训练，各射击10次的平均成绩相同，如果他们射击成绩的方差分别是 $S_{小刘}^{2} = 0.6$ ， $S_{小李}^{2} = 1.4$ ，那么两人中射击成绩比较稳定的是.

查看试题解析
12. 如图，将木条a ， b与c钉在一起，∠1＝70°，∠2＝50°，要使木条a与b平行，木条a旋转的度数至少是．

查看试题解析
13. 如图所示的各图表示由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有n（n＞1）盆花，每个图案花盆的总数为s．按此规律推断，以s、n为未知数的二元一次方程为．

查看试题解析

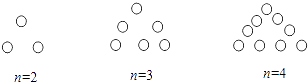
三、解答题

14. 计算： $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$

查看试题解析
15. 解方程组 $\{\begin{cases} 4 x + y - 1 = 0 \\ 2 y - 2 x + 1 = 0 \end{cases}$

查看试题解析
16. 如图， $A B ∥ C D$ ，P为 $A B$ ， $C D$ 之间的一点，已知 $∠ 2 = 28 °$ ， $∠ B P C = 58 °$ ，求∠1的度数.

查看试题解析
17. 如图，在直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5），请回答下列问题：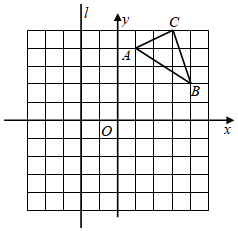

（1）画出△ABC关于x轴的对称图形ΔA₁B₁C₁；直接写出A₁、B₁、C₁的坐标；
（2）如图，在直线 $l$ 上找一点M，使得AM+BM的值最小.（保留作图痕迹）

查看试题解析
18. 列方程（组）解应用题
为振兴农村经济，某县决定购买A，B两种药材幼苗发给农民栽种，已知购买2棵A种药材幼苗和3棵B种药材幼苗共需41元.购买8棵A种药材幼苗和9棵B种药材幼苗共需137元.问每棵A种药材幼苗和每棵B种药材幼苗的价格分别是多少元？

查看试题解析
19. 如图，在Rt△ABC中，∠C=90°，点D是AC上一点，∠BDC=45°，AB=13，BC=5.

(1)、求BD的长；

(2)、求AD的长.

查看试题解析
20. 已知y＋2与3x成正比例，当x＝1时，y的值为4.

(1)、求y与x之间的函数表达式；

(2)、若点(－1，a)，(2，b)是该函数图象上的两点，请利用一次函数的性质比较a，b的大小.

查看试题解析
21. 某公司用3000元购进两种货物，货物卖出后，一种货物的利润率是10%，另一种货物的利润率是11%，两种货物共获利315元，求该公司购进这两种货物所用的费用各为多少元.

查看试题解析

22. 某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的满分均为100分，前6名选手的得分如下：

序号	1号	2号	3号	4号	5号	6号
笔试成绩/分	85	92	84	90	84	80
面试成绩/分	90	88	86	90	80	85

根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩.（综合成绩的满分仍为100分）

(1)、这6名选手笔试成绩的众数是分.

(2)、现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比.

(3)、求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选.

查看试题解析

23. 两个一次函数的图象如图所示，

(1)、分别求出两个一次函数的解析式；

(2)、求出两个一次函数图象的交点C坐标；

(3)、求这两条直线与y轴围成△ABC的面积．

查看试题解析
24. 如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E，点F为AC延长线上的一点，连接DF.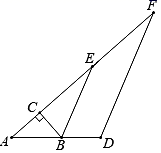

(1)、求∠CBE的度数；

(2)、若∠F=25°，求证：BE∥DF.

查看试题解析

25. 联合国《生物多样性公约》第十五次缔约方大会（ COP15 ）于2021年10月11日在云南昆明拉开帷幕，全球目光再次聚焦中国.中国将同各方共商全球生物多样性治理新战略，共同开启全球生物多样性治理新进程.生物多样性关系人类福祉，是人类赖以生存和发展的重要基础，为传播科学知识，鼓励同学们投身大自然去探索、发现大自然的神奇与美丽，从而尊重、热爱大自然，某中学团委联合生物社团共同举办了生物多样性科普知识竞赛.现从七、八年级中各随机抽取20名同学的竞赛成绩（百分制）进行整理和分析（成绩均为整数，成绩得分用x表示，共分成四个等级：A. x＜70，B. 70≤x≤80，C. 80≤x＜90，D. 90≤x≤100，其中成绩大于等于90的为优秀），下面给出了部分信息.
八年级抽取的20名学生的竞赛成绩在C等级中的数据分别是：82，83，85，87，87，88，89.

七，八年级抽取的学生竞赛成绩统计表

	平均数	中位数	众数	优秀率
七年级	83.35	83.5	89	25%
八年级	86.25	n	92	40%

根据以上信息，解答下列问题：

(1)、请补全条形统计图，并直接写出m、n的值；

(2)、根据以上数据分析，你认为哪个年级的竞赛成绩更好，并说明理由（写出一条理由即可）；

(3)、已知该校八年级共有720名学生参与了知识竞赛，请估计八年级竞赛成绩不低于80分的学生人数是多少？

查看试题解析

26. 问题情景：如图1，在同一平面内，点B和点C分别位于一块直角三角板 $P M N$ 的两条直角边 $P M$ ， $P N$ 上，点A与点P在直线 $B C$ 的同侧，若点P在 $Δ A B C$ 内部，试问 $∠ A B P$ ， $∠ A C P$ 与 $∠ A$ 的大小是否满足某种确定的数量关系？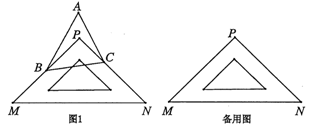

(1)、特殊探究：若 $∠ A = 55 °$ ，则 $∠ A B C + ∠ A C B =$ 度， $∠ P B C + ∠ P C B =$ 度， $∠ A B P + ∠ A C P =$ 度；

(2)、类比探索：请猜想 $∠ A B P + ∠ A C P$ 与 $∠ A$ 的关系，并说明理由；

(3)、类比延伸：改变点A的位置，使点P在 $Δ A B C$ 外，其它条件都不变，判断（2）中的结论是否仍然成立？若成立，请说明理由；若不成立，请直接写出 $∠ A B P$ ， $∠ A C P$ 与 $∠ A$ 满足的数量关系式．

查看试题解析