湖南省长沙市长郡教育集团2021-2022学年八年级上学期期末考试数学试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在一些美术字中，有的汉字是轴对称图形.下面4个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（　　）

A、 $3 + \sqrt{3} = 3 \sqrt{3}$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{12} = \pm 2 \sqrt{3}$ D、 $\sqrt{3} + \sqrt{12} = 3 \sqrt{3}$

查看试题解析
3. 若点 $A (x ， 1)$ 与 $B (- 2 ， y)$ 关于 $x$ 轴对称，则（）．

A、 $x = - 2$ ， $y = 1$ B、 $x = - 2$ ， $y = - 1$ C、 $x = 2$ ， $y = - 1$ D、 $x = 2$ ， $y = 1$

查看试题解析
4. 下列运算中，正确的是（　　　）

A、 $a^{6} \div a^{2} = a^{4}$ B、 $a^{2} + a^{3} = a^{5}$ C、 $a \cdot a^{3} = a^{3}$ D、 ${(a^{3})}^{3} = a^{6}$

查看试题解析
5. 在实数范围内要使 $\sqrt{{(a - 2)}^{2}} = a - 2$ 成立，则a的取值范围是（　　　）

A、a=2 B、 $a > 2$ C、 $a \geq 2$ D、 $a \leq 2$

查看试题解析
6. 如图， $O C$ 平分 $∠ A O B$ ，点P在 $O C$ 上，且 $P D ⊥ O B$ ，垂足为D，若 $P D = 3 cm$ ，则P到 $O A$ 的距离d满足（）

A、 $d < 3 cm$ B、 $d = 3 cm$ C、 $d > 3 cm$ D、无法确定

查看试题解析
7. 如图， $A B = D B$ ， $B C = B E$ ，欲证 $△ A B E ≌ △ D B C$ ，则可增加的条件是（）

A、 $∠ A B E = ∠ D B E$ B、 $∠ A = ∠ D$ C、 $∠ E = ∠ C$ D、 $∠ A B D = ∠ E B C$

查看试题解析
8. 在创建文明城市的进程中，某市为美化城市环境，计划种植树木50万棵，由于志愿者的加入，实际每天植树比原计划多30%，结果提前2天完成任务，设原计划每天植树 $x$ 万棵，由题意得到的方程是（）

A、 $\frac{50}{x} - \frac{50}{(1 + 30 %) x} = 2$ B、 $\frac{50}{x} - \frac{50}{30 % x} = 2$ C、 $\frac{50}{30 % x} - 2 = \frac{50}{x}$ D、 $\frac{50}{(1 + 30 %) x} - \frac{50}{x} = 2$

查看试题解析
9. 如图，B在AC上，D在CE上， $A D = B D = B C$ ， $∠ A C E = 25 °$ ， $∠ A D E$ 的度数为（）

A、50° B、65° C、75° D、80°

查看试题解析
10. 如图，等边 $△ A B C$ 中，D为AC中点，点P、Q分别为AB、AD上的点， $B P = A Q = 4$ ， $Q D = 3$ ，在BD上有一动点E，则 $P E + Q E$ 的最小值为（）

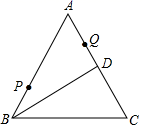A、7 B、8 C、10 D、12

查看试题解析

二、填空题

11. 若 $\frac{\sqrt{x - 1}}{2 - x}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
12. 如图， $∠ A B C$ 、 $∠ A C B$ 的平分线相交于点F，过F作 $D E // B C$ ，交 $A B$ 于点D，交 $A C$ 于点E， $B D = 3 cm$ ， $E C = 2 cm$ ，则 $D E =$ $cm$ .

查看试题解析
13. 已知 $3^{3 x + 1} = 81$ ，则 $x =$ .

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $∠ C = 30 °$ ，DE垂直平分AC，交BC于点E， $C E = 2$ ，则 $B C =$ .

查看试题解析
15. 已知（a﹣b）²＝6，（a+b）²＝4，则a²+b²的值为．

查看试题解析
16. 若3x﹣4y﹣z=0，2x+y﹣8z=0，则 $\frac{x^{2} + y^{2} + z^{2}}{x y - y z + x z}$ 的值为.

查看试题解析

三、解答题

17. 计算：
${(- \frac{1}{2})}^{- 1} - 2 + {(π - 3.14)}^{0}$

查看试题解析
18. 计算： $\sqrt{27}$ ﹣ $\sqrt{2} \times \sqrt{6}$ .

查看试题解析
19. 因式分解：

(1)、 $6 x^{2} - 3 x$ ；

(2)、 $9 a^{2} (x - y) + b^{2} (y - x)$ .

查看试题解析
20. 化简求值： ${(x + 2)}^{2} - (x - 1) (x + 1)$ ，其中 $x = - 1$ .

查看试题解析
21. 化简求值：（ $\frac{1}{a + 1} - \frac{a - 3}{a^{2} - 1}$ ）÷ $\frac{2}{a + 1}$ ，其中a＝ $\sqrt{2}$ +1.

查看试题解析
22. 如图， $D$ 是 $△ A B C$ 的边 $A B$ 上一点， $C F // A B$ ， $D F$ 交 $A C$ 于 $E$ 点， $D E = E F$ .

(1)、求证： $△ A D E$ ≌ $△ C F E$ ；

(2)、若 $A B = 5$ ， $C F = 4$ ，求 $B D$ 的长.

查看试题解析
23. 在 $Δ A B C$ 中，点E，点F分别是边AC，AB上的点，且 $A E = A F$ ，连结BE，CF交于点D， $∠ A B E = ∠ A C F$ .

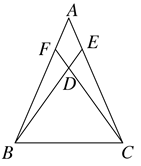(1)、求证： $Δ B C D$ 是等腰三角形.

(2)、若 $∠ A = 40^{\circ} ， B C = B D$ ，求 $∠ B E C$ 的度数.

查看试题解析
24. 如图， $△ A B C$ 为等边三角形，AE＝CD，AD，BE相交于点P，BQ⊥AD于Q，PQ＝3，PE＝1．

(1)、求证：BE＝AD；

(2)、求AD的长．

查看试题解析
25. “七一”建党节前夕，某校决定购买A，B两种奖品，用于表彰在“童心向党”活动中表现突出的学生.已知A奖品比B奖品每件多25元预算资金为1700元，其中800元购买A奖品，其余资金购买B奖品，且购买B奖品的数量是A奖品的3倍.

(1)、求A，B奖品的单价；

(2)、购买当日，正逢该店搞促销活动，所有商品均按原价八折销售，学校调整了购买方案：不超过预算资金且购买A奖品的资金不少于720元，A，B两种奖品共100件.求购买A，B两种奖品的数量，有哪几种方案？

查看试题解析
26. 阅读材料：在处理分数和分式的问题时，有时由于分子大于分母，或分子的次数高于分母的次数，在实际运算时难度较大，这时，我们可将分数（分式）拆分成一个整数（整式）与一个真分数（真分式）的和（差）的形式，通过对它的简单分析来解决问题，我们称这种方法为分离常数法，此法在处理分式或整除问题时颇为有效.
将分式分离常数可类比假分数变形带分数的方法进行，如： $\frac{x^{2} - 2 x + 3}{x - 1} = \frac{x (x - 1) + x - 2 x + 3}{x - 1} = x +$ $\frac{- (x - 1) + 2}{x - 1} = x - 1 + \frac{2}{x - 1}$ ，这样，分式就拆分成一个分式 $\frac{2}{x - 1}$ 与一个整式 $x - 1$ 的和的形式.

根据以上阅读材料，解答下列问题：

(1)、若x为整数， $\frac{x + 6}{x + 4}$ 为负整数，可求得 x最大值= ；

(2)、利用分离常数法，求分式 $\frac{2 x^{2} + 5}{x^{2} + 1}$ 的取值范围；

(3)、若分式 $\frac{5 x^{2} + 9 x - 3}{x + 2}$ 拆分成一个整式与一个真分式（分子为整数）的和（差）的形式为： $5 m - 11 + \frac{1}{n - 6}$ （整式部分对应等于 $5 m - 11$ ，真分式部分对应等于 $\frac{1}{n - 6}$ ）.
①用含x的式子表示出mn；

②随着x的变化， $m^{2} + n^{2} + m n$ 有无最小值？如有，最小值为多少？

查看试题解析
27. 如图1，在平面直角坐标系中，点 $A (a ， 0)$ 在x轴负半轴上，点B在y轴正半轴上，设 $A B = b$ ，且 $b^{2} - 4 a^{2} = 0$ .

(1)、直接写出 $∠ B A O$ 的度数.

(2)、如图2，点D为AB的中点，点P为y轴负半轴上一点，以AP为边作等边三角形APQ，连接DQ并延长交x轴于点M，若 $A B = 6$ ，求点M的坐标.

(3)、如图3，点C与点A关于y轴对称，点E为OC的中点，连接BE，过点B作 $∠ C B F = ∠ A E B$ ，且 $B F = B E$ ，连接AF交BC于点P，求 $\frac{B P}{C P}$ 的值.

查看试题解析