湖南省张家界市永定区2021-2022学年八年级上学期期末考试数学试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，是分式的是（）

A、 $\frac{2}{π}$ B、 $\frac{3}{x - 1}$ C、 $\frac{b}{3}$ D、 $\frac{y}{2} + 1$

查看试题解析
2. 已知线段 a＝2cm，b＝4cm，则下列长度的线段中，能与 a，b组成三角形的是（）

A、2cm B、4cm C、6cm D、8cm

查看试题解析
3. 成人每天维生素D的摄入量约为0.00000046克，将数据0.00000046用科学记数法表示为（）

A、 $4.6 \times 10^{- 6}$ B、 $4.6 \times 10^{- 7}$ C、 $0.46 \times 10^{- 6}$ D、 $46 \times 10^{- 6}$

查看试题解析
4. 如图，若AB=AC，则添加下列一个条件后，仍无法判定△ABE≌△ACD的是（）

A、 $∠ B = ∠ C$ B、BD=CE C、 $B E = C D$ D、∠AEB=∠ADC

查看试题解析
5. 如果式子 $\sqrt{2 x + 6}$ 有意义，那么x的取值范围在数轴上表示出来，正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 下列命题是真命题的是（）

A、等腰三角形的角平分线、中线、高线互相重合 B、一个三角形被截成两个三角形，每个三角形的内角和是90度 C、有两个角是60°的三角形是等边三角形 D、在 $△$ ABC中， $∠ A = ∠ B = 2 ∠ C$ ，则 $△$ ABC为直角三角形

查看试题解析
7. 关于x的方程 $\frac{m - 1}{x - 1} + \frac{x}{1 - x} = 0$ 有增根，则m的值是（）

A、2 B、1 C、0 D、-1

查看试题解析
8. 某商店为了促销一种定价为3元的商品，采取下列方式优惠销售：若一次性购买不超过5件，按原价付款；若一次性购买5件以上，超过部分按原价八折付款.如果小明有30元钱，那么他最多可以购买该商品（　　）

A、9件 B、10件 C、11件 D、12件

查看试题解析

二、填空题

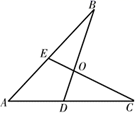
9. 如图，已知 $△$ ABD≌ $△$ ACE，∠A＝53°，∠B＝21°，则∠BEC＝°.

查看试题解析
10. 一个正数的平方根分别是 $x + 1$ 和 $x - 5$ ，则 $x =$ .

查看试题解析
11. 把命题“等边对等角”改写成“如果…，那么…”的形式是：．

查看试题解析
12. 若 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ，则 $\frac{a + b}{b + 2 c}$ ＝.

查看试题解析
13. 在 $△$ ABC中，AD⊥BC于点D，BD＝CD，若BC＝6，AD＝4，则图中阴影部分的面积为.

查看试题解析

三、解答题

14. 计算： ${(- \frac{1}{2})}^{- 1} - {(π - 3.14)}^{0} + | - \frac{1}{9} | \times 3^{3}$

查看试题解析
15. 求不等式组 ${\begin{matrix} 3 (x + 2) > x + 10 \\ \frac{x}{4} \geq \frac{x - 1}{3} \end{matrix}$ 的整数解.

查看试题解析
16. 化简式子（ $\frac{a^{2} - 2 a}{a^{2} - 4 a + 4} +$ 1） $\div \frac{a^{2} - 1}{a^{2} + a}$ ，并在﹣2，﹣1，0，1，2中选取一个合适的数作为a的值代入求值.

查看试题解析
17. 已知 $| x - 1 | + \sqrt{x - 2 y + 5} = 0$ .

(1)、求x与y的值；

(2)、求x+y的算术平方根.

查看试题解析
18. 星期六，小明与妈妈到离家12km的张家界市博物馆参观.小明从家骑自行车先走，1h后妈妈骑摩托车从家出发，沿相同路线前往博物馆，结果他们同时到达.已知妈妈骑摩托车的平均速度是小明骑自行车平均速度的3倍，求妈妈骑摩托车的平均速度.

查看试题解析
19. 已知：如图 $△$ ABC中，AB=AC=10，BC=8，∠A=39°，AB的垂直平分线MN交AC于D，交AB于M，连接BD.

求：

(1)、∠DBC的度数；

(2)、△BDC的周长.

查看试题解析
20. 材料1：因为无理数是无限不循环小数，所以无理数的小数部分我们不可能全部写出来.比如：π， $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确.
材料2：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是2.5−2得来的.

材料3：任何一个无理数，都夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ .

根据上述材料，回答下列问题：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是.

(2)、 $5 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 5 + \sqrt{3} < b$ ，求 $a + b$ 的值.

(3)、已知 $3 + \sqrt{3} = x + y$ ，其中x是整数，且0＜y＜1，求x+4y的倒数.

查看试题解析
21. 如图1，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连接AC和BD，相交于点E，连接BC.

(1)、求证 $△$ DOB≌ $△$ AOC；

(2)、求∠CEB的大小；

(3)、如图2， $△$ OAB固定不动，保持△OCD的形状和大小不变，将 $△$ OCD绕点O旋转（ $△$ OAB和 $△$ OCD不能重叠），求∠CEB的大小.

查看试题解析