湖南省岳阳市经济技术开发区2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{x - 1}$ 在实数范围内有意义，则实数x的取值范围是（）

A、 $x \geq - 1$ B、 $x \neq 0$ C、 $x \geq 1$ D、 $x > 0$

查看试题解析
2. 下列计算正确的是(　　)

A、 ${(a^{3})}^{2} = a^{5}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 $a^{7} \cdot a^{- 4} = a^{3}$ D、 ${(a^{- 2})}^{- 3} = a^{- 6}$

查看试题解析
3. 下列分式中，是最简分式的是（）

A、 $\frac{2 (x + 1)}{x + 1}$ B、 $\frac{a - b}{a + b}$ C、 $\frac{2 a x}{3 a y}$ D、 $\frac{a^{2} - b^{2}}{a - b}$

查看试题解析
4. 下列计算正确的是（）

A、 ${(2 \sqrt{2})}^{2} = 4 \sqrt{2}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{12} \div \sqrt{3} = 4$

查看试题解析
5. 尺规作图：作 $∠ A^{'} O^{'} B^{'}$ 角等于已知角 $∠ A O B$ .示意图如图所示，则说明 $∠ A^{'} O^{'} B^{'} = ∠ A O B$ 的依据是（）

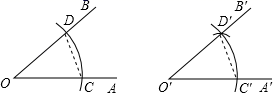A、SSS B、SAS C、ASA D、AAS

查看试题解析
6. 在3.14，0， $- \frac{π}{5}$ ， $\sqrt{2}$ ， $- \frac{1}{4}$ ，2.010010001…（每两个1之间的0依次增加1个）这六个数中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 在数轴上表示某不等式组的解集，如图所示，则这个不等式组可能是（）

A、 ${\begin{array}{l} 2 x - 4 > x \\ x + 1 \geq 0 \end{array}$ B、 ${\begin{array}{l} 2 x - 4 > x \\ x + 1 \leq 0 \end{array}$ C、 ${\begin{array}{l} 2 x - 4 < x \\ x + 1 \leq 0 \end{array}$ D、 ${\begin{array}{l} 2 x - 4 < x \\ x + 1 \geq 0 \end{array}$

查看试题解析
8. 如图，在△ABC中，AD为∠BAC的平分线，BM⊥AD，垂足为M，且AB=5，BM=2，AC=9，则∠ABC与∠C的关系为（）

A、∠ABC=2∠C B、∠ABC= $\frac{5}{2}$ ∠C C、 $\frac{1}{4}$ ∠ABC=∠C D、∠ABC=3∠C

查看试题解析

二、填空题

9. 生物学家发现一种病毒的长度约为0.0000603毫米，用科学记数法表示为毫米；

查看试题解析
10. 不等式 $3 x - 5 > 1$ 的最小整数解是.

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 35 °$ ，线段AB的垂直平分线MN与AB交于点E，与BC交于点D，连接AD，则 $∠ D A C =$ 度.

查看试题解析
12. 当 $a = 3 \sqrt{2}$ ， $b = \sqrt{8}$ 时，则 $a + b$ 的值为.

查看试题解析
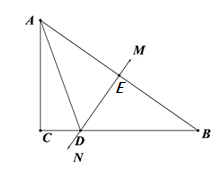13. 若关于x的方程 $\frac{x + 1}{x - 2} = \frac{m}{x - 2}$ 有增根，则m的值是.

查看试题解析
14. 用海伦公式求面积的计算方法是： $S = \sqrt{p (p - a) (p - b) (p - c)}$ ，其中S表示三角形的面积，a，b，c分别表示三边之长，p表示周长的一半，即 $p = \frac{a + b + c}{2}$ .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致，所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 $△ A B C$ 中，已知三边之长 $a = 6$ ， $b = 7$ ， $c = 5$ ，则 $△ A B C$ 的面积为.

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，射线AF是 $∠ B A C$ 的平分线，交BC于点D，过点B作AB的垂线与射线AF交于点E，连结CE，M是DE的中点，连结BM并延长与AC的延长线交于点G.则下列结论正确的是.

① $△ B C G ≌ △ A C D$ ②BG垂直平分DE ③ $B E ⊥ C E$ ④ $∠ G = 2 ∠ G B E$ ⑤ $B E + C G = A C$

查看试题解析

三、解答题

16. 计算： $- 1^{2} + {(\sqrt{3} - 1)}^{0} + \sqrt{16} - {(\frac{1}{2})}^{- 1}$

查看试题解析
17. 求不等式组 ${\begin{cases} 5 x - 1 > 3 x - 4 \\ - \frac{1}{3} x \leq \frac{2}{3} - x \end{cases}$ 的解集.

查看试题解析
18. 先化简 $\frac{x + 1}{1 - x} \div (1 + \frac{x^{2} + x}{1 - x^{2}})$ ，再从 $- 1 < x < 2$ 的范围内选取一个合适的整数代入求值.

查看试题解析
19.
如图， △ABC中， AB=AC ，D、E分别是AB、AC上的点，且 ∠ABE=∠ACD ，BE、CD交于点O，求证： △OBC是等腰三角形.

查看试题解析
20. 已知：如图，点B，F在线段EC上， $A C = D F$ ， $A C ∥ D F$ ， $B E = C F$ .求证： $A B ∥ D E$ .

查看试题解析
21. 今年4月23日是第26个世界读书日.八（1）班举办了“让读书成为习惯，让书香飘满校园”主题活动.准备订购一批新的图书鲁迅文集（套）和四大名著（套）.

(1)、采购员从市场上了解到四大名著（套）的单价比鲁迅文集（套）的单价的贵25元.花费1000元购买鲁迅文集（套）的数量与花费1500元购买鲁迅文集（套）的数量相同.求鲁迅文集（套）和四大名著（套）的单价各是多少元？

(2)、若购买鲁迅文集和四大名著共10套（两类图书都要买），总费用不超过570元，问该班有哪几种购买方案？

查看试题解析
22. 王老师让同学们根据二次根式的相关内容编写一道题，以下是王老师选出的两道题和她自己编写的一道题.先阅读，再回答问题.

(1)、小青编的题，观察下列等式：
$\frac{2}{\sqrt{3} + 1} = \frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \frac{2 (\sqrt{3} - 1)}{3 - 1} = \sqrt{3} - 1$

$\frac{2}{\sqrt{5} + \sqrt{3}} = \frac{2 (\sqrt{5} - \sqrt{3})}{(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})} = \frac{2 (\sqrt{5} - \sqrt{3})}{{(\sqrt{5})}^{2} - {(\sqrt{3})}^{2}} = \frac{2 (\sqrt{5} - \sqrt{3})}{5 - 3} = \sqrt{5} - \sqrt{3}$

直接写出以下算式的结果：

$\frac{2}{\sqrt{7} + \sqrt{5}} =$ ； $\frac{2}{\sqrt{2 n + 1} + \sqrt{2 n - 1}}$ （n为正整数）＝；

(2)、小明编的题，由二次根式的乘法可知：
${(\sqrt{3} + 1)}^{2} = 4 + 2 \sqrt{3}$ ， ${(\sqrt{5} + \sqrt{3})}^{2} = 8 + 2 \sqrt{15}$ ， ${(\sqrt{a} + \sqrt{b})}^{2} = a + b + 2 \sqrt{a b} (a \geq 0 ， b \geq 0)$

再根据平方根的定义可得

$\sqrt{4 + 2 \sqrt{3}} = \sqrt{3} + 1$ ， $\sqrt{8 + 2 \sqrt{15}} = \sqrt{5} + \sqrt{3}$ ， $\sqrt{a + b + 2 \sqrt{a b}} = \sqrt{a} + \sqrt{b} (a \geq 0 ， b \geq 0)$

直接写出以下算式的结果：

$\sqrt{6 + 2 \sqrt{5}} =$ ， $\sqrt{4 - 2 \sqrt{3}} =$ ， $\sqrt{7 + 4 \sqrt{3}} =$ ：

(3)、王老师编的题，根据你的发现，完成以下计算：
$(\frac{2}{\sqrt{3} + 1} + \frac{2}{\sqrt{5} + \sqrt{3}} + \frac{2}{\sqrt{7} + \sqrt{5}} + \frac{2}{\sqrt{9} + \sqrt{7}} + \frac{2}{\sqrt{11} + \sqrt{9}}) \cdot \sqrt{12 + 2 \sqrt{11}}$

查看试题解析
23. 直线l经过点A， $△ A B C$ 在直线l上方， $A B = A C$ .

(1)、如图1， $∠ B A C = 90 °$ ，过点B，C作直线l的垂线，垂足分别为D、E.求证： $△ A B D ≌ △ C A E$

(2)、如图2，D，A，E三点在直线l上，若 $∠ B A C = ∠ B D A = ∠ A E C = α$ （ $α$ 为任意锐角或钝角），猜想线段DE、BD、CE有何数量关系？并给出证明.

(3)、如图3， $∠ B A C = 90 °$ 过点B作直线l上的垂线，垂足为F，点D是BF延长线上的一个动点，连结AD，作 $∠ D A E = 90 °$ ，使得 $A E = A D$ ，连结DE，CE.直线l与CE交于点G.求证：G是CE的中点.

查看试题解析