河南省洛阳市嵩县2021-2022学年八年级上学期期末考试数学试卷
试卷更新日期:2022-01-27 类型:期末考试
一、单选题
-
1. 下列统计图中,最宜反映气温变化的是( )A、折线统计图 B、条形统计图 C、扇形统计图 D、频数分布直方图2. 下列结论正确的是( )A、64的立方根是±4 B、1的平方根是1 C、算术平方根等于它本身的数只有0 D、 =﹣3. 等腰三角形的一个内角是 ,则它底角的度数是( )A、 B、 或 C、 或 D、4. 下列计算中错误的是( )A、4a5b3c2÷(﹣2a2bc)2=ab B、(a+1)(a﹣1)(a2+1)=a4﹣1 C、4x2y•(﹣ y)÷4x2y2=﹣ D、25×( x2﹣ x+1)=x2﹣ x+15. 如图, 是 的角平分线, 于点E, , , ,则 的长是( )
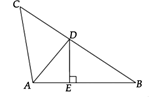 A、2 B、3 C、4 D、56. 如图,已知钓鱼竿 的长为 ,露在水面上的鱼线 长为 ,某钓鱼者想看看鱼钩上的情况,把鱼竿 转动到 的位置,此时露在水面上的鱼线 为 ,则 的长为( )
A、2 B、3 C、4 D、56. 如图,已知钓鱼竿 的长为 ,露在水面上的鱼线 长为 ,某钓鱼者想看看鱼钩上的情况,把鱼竿 转动到 的位置,此时露在水面上的鱼线 为 ,则 的长为( ) A、 B、 C、 D、7. 已知点P在 ABC的边BC上,且满足PA=PC , 则下列确定点P位置的尺规作图,正确的是( )A、
A、 B、 C、 D、7. 已知点P在 ABC的边BC上,且满足PA=PC , 则下列确定点P位置的尺规作图,正确的是( )A、 B、
B、 C、
C、 D、
D、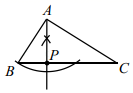 8. 如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
8. 如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( ) A、 B、 C、 D、9. 如图, 是等边三角形, 是中线,延长 至E,使 ,则下列结论错误的是( )
A、 B、 C、 D、9. 如图, 是等边三角形, 是中线,延长 至E,使 ,则下列结论错误的是( ) A、 B、 C、 D、10. 有一个边长为1的正方形,以它的一条边为斜边,向外作一个直角三角形,再分别以直角三角形的两条直角边为边,向外各作一个正方形,称为第一次“生长”(如图1);再分别以这两个正方形的边为斜边,向外各自作一个直角三角形,然后分别以这两个直角三角形的直角边为边,向外各作一个正方形,称为第二次“生长”(如图2)……如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( )
A、 B、 C、 D、10. 有一个边长为1的正方形,以它的一条边为斜边,向外作一个直角三角形,再分别以直角三角形的两条直角边为边,向外各作一个正方形,称为第一次“生长”(如图1);再分别以这两个正方形的边为斜边,向外各自作一个直角三角形,然后分别以这两个直角三角形的直角边为边,向外各作一个正方形,称为第二次“生长”(如图2)……如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( ) A、1 B、2020 C、2021 D、2022
A、1 B、2020 C、2021 D、2022二、填空题
-
11. 用反证法证明“已知,a⊥b,c⊥b,求证:a∥c”,第一步应先假设 .12. 若 ,则以a、b为边长的等腰三角形的周长为 .13. (x2﹣mx+6)(4x﹣2)的积中不含x的二次项,则m的值是 .14. 如图所示是小明一天24小时的作息时间分配的扇形统计图,那么他的阅读时间是小时.
 15. 如图,已知CB⊥AD , AE⊥CD , 垂足分别为B , E , AE、BC相交于点F , 若AB=BC=8,CF=2,连结DF , 则图中阴影部分面积为 .
15. 如图,已知CB⊥AD , AE⊥CD , 垂足分别为B , E , AE、BC相交于点F , 若AB=BC=8,CF=2,连结DF , 则图中阴影部分面积为 .
三、解答题
-
16.(1)、若 , .求 的值;(2)、先化简,再求值: ,其中 , .17. 如图,AB CD , CD交BF于E .
 (1)、尺规作图:以点D为顶点,射线DC为一边,在DC的右侧作∠CDG , 使∠CDG=∠B . (要求:不写作法,但保留作图痕迹)(2)、证明:DG BF .18. 如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
(1)、尺规作图:以点D为顶点,射线DC为一边,在DC的右侧作∠CDG , 使∠CDG=∠B . (要求:不写作法,但保留作图痕迹)(2)、证明:DG BF .18. 如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离. 19. 2021年10月10日是辛亥革命110周年纪念日.为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神,社区开展了系列纪念活动.如图,有一块四边形空地,社区计划将其布置成展区,陈列有关辛亥革命的历史图片.现测得 , , ,且 .
19. 2021年10月10日是辛亥革命110周年纪念日.为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神,社区开展了系列纪念活动.如图,有一块四边形空地,社区计划将其布置成展区,陈列有关辛亥革命的历史图片.现测得 , , ,且 . (1)、试说明 ;(2)、求四边形展区(阴影部分)的面积.20. 阅读下列材料:
(1)、试说明 ;(2)、求四边形展区(阴影部分)的面积.20. 阅读下列材料:材料1:将一个形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(+n)的形式,如x2+4x+3=(x+1)(x+3);x2﹣4x﹣12=(x﹣6)(x+2)
材料2:因式分解:(x+y)2+2(x+y)+1
解:将“x+y”看成一个整体,令x+y=A,则原式=A2+2A+1=(A+1)2 , 再将“A”还原,得原式=(x+y+1)2
上述解题方法用到“整体思想”,“整体思想”是数学解题中常见的一种思想方法.请你解答下列问题:
(1)、根据材料1,把x2﹣6x+8分解因式;(2)、结合材料1和材料2,完成下面小题:分解因式:(x﹣y)2+4(x﹣y)+321. 学校针对安阳市创建文明城市开展征文比赛(每位同学限一篇),每篇作品的成绩记为x分 ,学校从中随机抽取部分学生的成绩进行统计,并将统计结果绘制成如下不完整的统计图表.组别
分数段
频数
频率
甲
22
0.22
乙
a
0.4
丙
30
b
丁
8
0.08

根据以上信息,解答下列问题:
(1)、本次共抽取篇征文;(2)、填空: , ;(3)、请补全频数分布直方图;(4)、若全校共2400名同学参赛,请估计不低于80分的学生人数.

