贵州省六盘水市2021-2022学年七年级上学期第三次月考数学试卷
试卷更新日期:2022-01-27 类型:月考试卷
一、单选题
-
1. 下列各式中,错误的是( )A、 B、 C、 D、2. 下列各数中,最大的数是( )A、 B、 C、0 D、13. 第七次全国人口普查数据显示,贵州省常住人口约为3856.21万人,将38562100用科学记数法表示为( )A、 B、 C、 D、4. 如图是一个几何体的表面展开图,这个几何体是( )
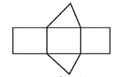 A、
A、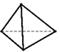 B、
B、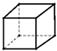 C、
C、 D、
D、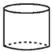 5. 如图, , , 平分 ,则 的度数为( )
5. 如图, , , 平分 ,则 的度数为( ) A、 B、 C、 D、6. 下列说法中,①一个有理数不是整数就是分数;②一个有理数不是正数,就是负数;③一个整数不是正的,就是负的;④一个分数不是正的,就是负的;⑤若 ,则 与 互为倒数;⑥ 且 , 异号,则 .正确的个数是( )A、3个 B、4个 C、5个 D、6个7. 如图,点B是线段AD的中点,C在线段BD上且满足BD=3CD,若图中所有线段的长度之和为30,则线段BC的长度为( ).
A、 B、 C、 D、6. 下列说法中,①一个有理数不是整数就是分数;②一个有理数不是正数,就是负数;③一个整数不是正的,就是负的;④一个分数不是正的,就是负的;⑤若 ,则 与 互为倒数;⑥ 且 , 异号,则 .正确的个数是( )A、3个 B、4个 C、5个 D、6个7. 如图,点B是线段AD的中点,C在线段BD上且满足BD=3CD,若图中所有线段的长度之和为30,则线段BC的长度为( ). A、1 B、2 C、3 D、48. 某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A、1 B、2 C、3 D、48. 某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( ) A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、经过直线外一点,有且只有一条直线与这条直线平行9. 商品的原售价为 元,若按该价的七五折出售,仍获利 ,则该商品的进价为( )元A、 B、 C、 D、10. 我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”意思是现有几个人共买一件物品,每人出8钱.多出3钱;每人出7钱,差4钱.问人数,物价各是多少?若设共有 人,物价是 钱,则下列方程正确的是( )A、 B、 C、 D、11.
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、经过直线外一点,有且只有一条直线与这条直线平行9. 商品的原售价为 元,若按该价的七五折出售,仍获利 ,则该商品的进价为( )元A、 B、 C、 D、10. 我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”意思是现有几个人共买一件物品,每人出8钱.多出3钱;每人出7钱,差4钱.问人数,物价各是多少?若设共有 人,物价是 钱,则下列方程正确的是( )A、 B、 C、 D、11.
对于有理数 , ,定义 ,则 化简后得( )A、 B、 C、 D、12. 如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为 ,第2幅图形中“●”的个数为 ,第3幅图形中“●”的个数为 ,…,以此类推,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图可以沿线折叠成一个带数字的立方体,每三个带数字的面交于立方体的一个顶点,则相交于一个顶点的三个面上的数字之和最小是.
 14. 若 ,则 .15. 古希腊数学家把数 ,…叫做三角数,它有一定的规律性,若把第一个三角数记为 ,第二个三角数记为 ,…,第 个三角数记为 ,计算 的值为.
14. 若 ,则 .15. 古希腊数学家把数 ,…叫做三角数,它有一定的规律性,若把第一个三角数记为 ,第二个三角数记为 ,…,第 个三角数记为 ,计算 的值为.三、解答题
-
16. 计算:(1)、 ;(2)、 .17. 用数轴上的点表示下列各数: , , ,0, ,并用“<”把它们连接起来.
 18. 阅读:因为一个非负数的绝对值等于它本身,负数的绝对值等于它的相反数,所以当 时 ,当 时 ,根据以上阅读完成:(1)、 ;(2)、计算: .19. “整体思想”是中学数学学习中的一种重要思想,它在多项式的化简与求值中应用极为广泛,例如把 看成一个整体: ,请应用整体思想解答下列问题:(1)、化简: ;(2)、已知 , , ,求 的值.20. 在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
18. 阅读:因为一个非负数的绝对值等于它本身,负数的绝对值等于它的相反数,所以当 时 ,当 时 ,根据以上阅读完成:(1)、 ;(2)、计算: .19. “整体思想”是中学数学学习中的一种重要思想,它在多项式的化简与求值中应用极为广泛,例如把 看成一个整体: ,请应用整体思想解答下列问题:(1)、化简: ;(2)、已知 , , ,求 的值.20. 在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p. (1)、若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?(2)、若原点O在图中数轴上点C的右边,且CO=28,求p.21. 如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).
(1)、若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?(2)、若原点O在图中数轴上点C的右边,且CO=28,求p.21. 如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分). (1)、用含字母x的式子表示:草坪的长a=米,宽b=米;(2)、请求出草坪的周长;(3)、当小路的宽为1米时,草坪的周长是多少?22. 某城市高铁站与汽车站之间刚好由一段东西方向的道路连接,为保障市民的出行安全,公安部门每晚派一辆警车在这段东西向的公路来回巡查,若规定向东为正,向西为负,行驶的路程(千米)用正负数表示如下: , , , , , , ;(1)、这辆车最后在出发点的哪个方向?离出发点多远?(2)、这辆车最远离出发点多远?(3)、若在行驶过程中,平均每千米消耗汽油0.07升,在这过程中,这辆车一共消耗汽油多少升?23. 现有甲、乙两个瓷器店,出售茶壶和茶杯,茶壶每只价格20元,茶杯每只5元,已知甲店制定的优惠方法是:买一只茶壶送一只茶杯,乙店为总价的 90%付款,现某单位需购买茶壶10只,茶杯若干只(不少于10只):(1)、当购买茶杯多少时,两种优惠方法一样?(2)、当购买40只茶杯时,请聪明的你去办这件事,你打算怎样购买更省钱?请通过计算说明理由.24. 如图,O为直线AB上的一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°),的直角顶点放在O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方,将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.
(1)、用含字母x的式子表示:草坪的长a=米,宽b=米;(2)、请求出草坪的周长;(3)、当小路的宽为1米时,草坪的周长是多少?22. 某城市高铁站与汽车站之间刚好由一段东西方向的道路连接,为保障市民的出行安全,公安部门每晚派一辆警车在这段东西向的公路来回巡查,若规定向东为正,向西为负,行驶的路程(千米)用正负数表示如下: , , , , , , ;(1)、这辆车最后在出发点的哪个方向?离出发点多远?(2)、这辆车最远离出发点多远?(3)、若在行驶过程中,平均每千米消耗汽油0.07升,在这过程中,这辆车一共消耗汽油多少升?23. 现有甲、乙两个瓷器店,出售茶壶和茶杯,茶壶每只价格20元,茶杯每只5元,已知甲店制定的优惠方法是:买一只茶壶送一只茶杯,乙店为总价的 90%付款,现某单位需购买茶壶10只,茶杯若干只(不少于10只):(1)、当购买茶杯多少时,两种优惠方法一样?(2)、当购买40只茶杯时,请聪明的你去办这件事,你打算怎样购买更省钱?请通过计算说明理由.24. 如图,O为直线AB上的一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°),的直角顶点放在O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方,将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周. (1)、几秒后ON与OC重合?(2)、如图2,经过t秒后,OM恰好平分∠BOC,求此时t的值.(3)、若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC平分∠MOB?请画出图并说明理由.
(1)、几秒后ON与OC重合?(2)、如图2,经过t秒后,OM恰好平分∠BOC,求此时t的值.(3)、若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC平分∠MOB?请画出图并说明理由.