贵州省六盘水市2021-2022学年八年级上学期第三次月考数学试卷

试卷更新日期：2022-01-27 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列实数中，最大的数是（）

A、 $π$ B、 $\sqrt{2}$ C、 $| - 2 |$ D、3

查看试题解析
2. 满足下列条件的△ABC中，不是直角三角形的是（）

A、∠A＝∠B－∠C B、∠A︰∠B︰∠C＝1︰1︰2 C、a︰b︰c＝1︰1︰2 D、b²＝c²－a²

查看试题解析
3. 如果点A（3， $m + 2$ ）在x轴上，那么点B（ $m + 1$ ， $m - 3$ ）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知关于x、y的二元一次方程组 ${\begin{array}{l} a x - y = 4 \\ 3 x + b y = 4 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$ ，则 $a + b$ 的值是（）

A、1 B、2 C、﹣1 D、0

查看试题解析
5. 在勾股定理的学习过程中，我们已经学会了运用以下图形，验证著名的勾股定理：这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”．实际上它也可用于验证数与代数，图形与几何等领域中的许多数学公式和规律，它体现的数学思想是（）

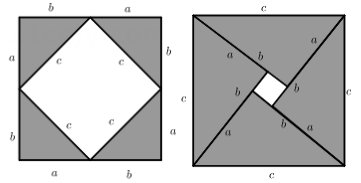A、统计思想 B、分类思想 C、数形结合思想 D、函数思想

查看试题解析
6. 下列判断：①10的平方根是± $\sqrt{10}$ ；② $\sqrt[3]{6}$ 与 $\sqrt[3]{- 6}$ 互为相反数；③0.1的算术平方根是0.01；④（ $\sqrt[3]{a}$ ）³＝a；⑤ $\sqrt{a^{4}}$ ＝±a².其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在4×4的正方形网格中，每个小正方形的边长均为1，点A，B，C都在格点上，AD⊥BC于点D，则AD的长为（　　）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{5}$ D、3

查看试题解析
8. 实数a，b在数轴上对应的位置如图所示，化简|a﹣b|﹣ $\sqrt{b^{2}}$ 的结果是（　　）

A、a B、﹣a C、2b D、2b﹣a

查看试题解析
9. y₁＝ax+b和y₂＝bx+a（a≠b），函数y₁和y₂的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
10. 《九章算术》卷八方程第十题原文为：“今有甲、乙二人持钱不知其数.甲得乙半而钱五十，乙得甲太半而亦钱五十.问：甲、乙持钱各几何？”题目大意是：甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半，那么甲共有钱50；如果乙得到甲所有钱的 $\frac{2}{3}$ ，那么乙也共有钱50.问：甲，乙两人各带了多少钱？设甲，乙两人持钱的数量分别为x，y，则可列方程组为（　　）

A、 ${\begin{array}{l} 2 x + y = 50 \\ x + \frac{2}{3} y = 50 \end{array}$ B、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ C、 ${\begin{array}{l} x - \frac{1}{2} y = 50 \\ x - \frac{2}{3} y = 50 \end{array}$ D、 ${\begin{array}{l} 2 x - y = 50 \\ x - \frac{2}{3} y = 50 \end{array}$

查看试题解析
11. 在平面直角坐标系内，一次函数y＝k₁x+b₁与y＝k₂x+b₂的图象如图所示，则关于x，y的方程组 ${\begin{array}{l} y - k_{1} x = b_{1} \\ y - k_{2} x = b_{2} \end{array}$ 的解是（　　）

A、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 2 \end{array}$

查看试题解析
12. 在平面直角坐标系中，李明做走棋游戏，其走法是：棋子从原点出发，第1步向右走1个单位长度，第2步向右走2个单位长度，第3步向上走1个单位长度，第4步向右走1个单位长度……依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位长度；当n被3除，余数是1时，则向右走1个单位长度；当n被3除，余数是2时，则向右走2个单位长度.当走完第12步时，棋子所处位置的坐标是（　　）

A、（9，3） B、（9，4） C、（12，3） D、（12，4）

查看试题解析

二、填空题

13. 如图，正方形OABC的边OC落在数轴上，OC＝2，以O为圆心，OB长为半径作圆弧与数轴交于点D，则点D表示的数是 .

查看试题解析
14. 已知43²＝1849，44²＝1936，45²＝2025，46²＝2116，若n为整数，且n＜ $\sqrt{2021}$ ＜n+1，则n的值为 .

查看试题解析
15. 如图，已知圆柱的底面直径 $B C = \frac{6}{π}$ ，高 $A B = 3$ ，小虫在圆柱表面爬行，从点 $C$ 爬到点 $A$ ，然后在沿另一面爬回点 $C$ ，则小虫爬行的最短路程为.

查看试题解析
16. 某人购进一批苹果到集贸市场零售，已知卖出的苹果数量与售价之间的关系如图所示，成本为5元/千克，现以8元/千克卖出，赚元．

查看试题解析

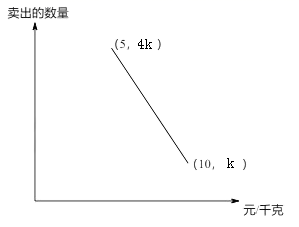
三、解答题

17. 计算下列各题：

(1)、 $3 \sqrt{3} - \frac{1}{2} \sqrt{8} \div \sqrt{2} - \frac{3}{4} \sqrt{48}$ ；

(2)、 ${\begin{array}{l} 3 x - y = - 4 \\ x - 2 y = - 3 \end{array}$ .

查看试题解析
18. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做“格点”，以格点为顶点分别按下列要求画三角形：

(1)、在图①中画出一个钝角三角形，使它的面积为4，并求出该三角形的三边长；

(2)、在图②中画出一个面积为10的正方形.

查看试题解析
19. 如图所示，六盘水市某中学有一块不规则四边形的空地ABCD，学校计划在空地上铺悬浮地板，经测量，∠ABC＝90°，BC＝6m，AB＝8m，AD＝26m，CD＝24m.

(1)、求空地ABCD的面积.

(2)、若每铺1平方米悬浮地板需要120元，问总共需投入多少元？

查看试题解析
20. 阅读材料：
∵ $\sqrt{4}$ ＜ $\sqrt{5}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{5}$ ＜3，

∴0＜ $\sqrt{5}$ ﹣2＜1，

∴ $\sqrt{5}$ 的整数部分为2， $\sqrt{5}$ 的小数部分为 $\sqrt{5}$ ﹣2.

解决问题：

(1)、填空： $\sqrt{19}$ 的小数部分是；

(2)、已知a是 $\sqrt{90}$ 的整数部分，b是 $\sqrt{3}$ 的小数部分，求a+b﹣ $\sqrt{3}$ 的立方根.

查看试题解析
21. 如图，在平面直角坐标系中，已知线段AB；

（1）请在y轴上找到点C，使△ABC的周长最小，画出△ABC，并写出点C的坐标；
（2）作出△ABC关于y轴对称的△A'B'C'；
（3）连接BB'，AA'.求四边形AA'B'B的面积.

查看试题解析
22. 在平面直角坐标系中，一次函数y＝kx+b（k≠0）的图象由函数y＝ $\frac{1}{2}$ x的图象向下平移1个单位长度得到.

(1)、求这个一次函数的解析式；

(2)、求一次函数与x轴，y轴的交点坐标.

查看试题解析
23. 如图，在Rt△ABC中，∠ACB＝90°，AB＝20cm，AC＝16cm，点P从点A出发，以每秒1cm的速度向点C运动，连接PB，设运动时间为t秒（t＞0）.

(1)、当△PBC的面积为△ABC面积的一半时，求t的值；

(2)、当t为何值时，AP＝PB.

查看试题解析
24. 六盘水市某中学准备购买一批笔袋奖励优秀学生.现文具店有A、B两种笔袋供选择，已知2个A笔袋和3个B笔袋的价格相同；而购买1个A笔袋和2个B笔袋共需35元.

(1)、求A、B两种笔袋的单价；

(2)、根据需要，学校共需购买40个笔袋，该文具店为了支持学校工作，给出了如下两种大幅优惠方案：
方案一：A种笔袋八折、B种笔袋六折；
方案二：A、B两种笔袋都七折.
设购买A种笔袋个数为a（a≥0）个，购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式；
②购买A种笔袋多少个时，两种方案所需费用一样多.

查看试题解析
25. 疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $a$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $y$ （万人）与各自接种时间 $x$ （天）之间的关系如图所示．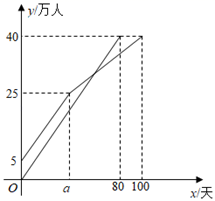

(1)、直接写出乙地每天接种的人数及 $a$ 的值；

(2)、当甲地接种速度放缓后，求 $y$ 关于 $x$ 的函数解析式，并写出自变量 $x$ 的取值范围；

(3)、当乙地完成接种任务时，求甲地未接种疫苗的人数．

查看试题解析