河南省安阳市林州市2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-01-27 类型：期末考试

进入出卷网下载

一、单选题

1. 低碳环保理念深入人心，共享单车已成为出行新方式．下列共享单车图标，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知一粒大米的质量约为0.000021千克，这个数用科学记数法表示为（　　）

A、0.21×10^﹣4 B、2.1×10^﹣4 C、0.21×10^﹣5 D、2.1×10^﹣⁵

查看试题解析
3. 若分式 $\frac{1}{a - 1}$ 有意义，则a的取值范围是（）

A、a≠1 B、a≠0 C、a≠1且a≠0 D、一切实数

查看试题解析
4. 将一副三角板按如图所示的方式放置，图中∠CAF的大小等于（）

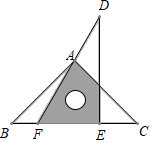A、50° B、60° C、75° D、85°

查看试题解析
5. 下列计算正确的是（　　）

A、（a²b）²=a²b² B、a⁶÷a²=a³ C、（3xy²）²=6x²y⁴ D、（﹣m）⁷÷（﹣m）²=﹣m⁵

查看试题解析
6. 如图，测河两岸A，B两点的距离时，先在AB的垂线BF上取C，D两点，使CD＝BC，再过点D画出BF的垂线DE，当点A，C，E在同一直线上时，可证明△EDC≌△ABC，从而得到ED＝AB，测得ED的长就是A，B的距离，判定△EDC≌△ABC的依据是：（）

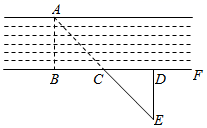A、ASA B、SSS C、AAS D、SAS

查看试题解析
7. 有一段全长为800米的公路，路面需整改，为了尽量减少施工对城市交通所造成的影响，实际施工时，每天的功效比原计划增加10%，结果提前3天完成这一任务，设原计划每天整改x米，则下列方程正确的是（）

A、 $\frac{800}{(1 + 10 %) x} - \frac{800}{x} = 3$ B、 $\frac{800}{(1 - 10 %) x} - \frac{800}{x} = 3$ C、 $\frac{800}{x} - \frac{800}{(1 + 10 %) x} = 3$ D、 $\frac{800}{x} - \frac{800}{(1 - 10 %) x} = 3$

查看试题解析
8. 如图，在△ABC和△DEC中，已知CB=CE，还需添加两个条件才能使△ABC≌△ DEC，不能添加的一组条件是（）

A、AC=DC，AB=DE B、AC=DC， ∠A=∠D C、AB=DE，∠B=∠E D、∠ACD=∠BCE，∠B=∠E

查看试题解析
9. 如图，在边长为a的正方形中，剪去一个边长为b的小正方形（ $a > b > 0$ ），将余下部分对称剪开，拼成一个平行四边形，根据两个图形阴影部分面积的关系，可以得到一个关于a，b的恒等式是（）

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $a^{2} - b^{2} = (a + b) (a - b)$ D、 $a (a - b) = a^{2} - a b$

查看试题解析
10. 如图，点D，E，F分别在 $△ A B C$ 的边 $A B$ ， $B C$ ， $C A$ 上（不与顶点重合），设 $∠ B A C = α$ ， $∠ F E D = θ$ .若 $△ B E D ≌ △ C F E$ ，则 $α$ ， $θ$ 满足的关系是（）

A、 $α + θ = 90 °$ B、 $α + 2 θ = 180 °$ C、 $α - θ = 90 °$ D、 $2 α + θ = 180 °$

查看试题解析

二、填空题

11. 计算： ${(\frac{1}{3})}^{- 1} + {(- 2)}^{0} =$ .

查看试题解析
12. 一个多边形的内角和是它的外角和的4倍，则这个多边形的边数是．

查看试题解析
13. 在平面直角坐标系中，已知 $A (0 ， 0)$ ， $B (3 ， 0)$ ， $C (1 ， 2)$ ，若 $△ B A D ≌ △ A B C$ ，则点D的坐标为.

查看试题解析
14. 已知 $x - y = 2$ ， $x y = - 1$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
15. 如图，在锐角三角形ABC中，AB=4，△ABC的面积为10，BD平分∠ABC，若M、N分别是BD、BC上的动点，则CM＋MN的最小值为

查看试题解析

三、解答题

16. 计算或因式分解：

(1)、计算：（a²﹣4） $\div \frac{a + 2}{a}$ ；

(2)、因式分解：a²（x﹣y）+b²（y﹣x）.

查看试题解析
17. 已知：如图，点A、B、C、D在一条直线上，FB∥EA交EC于H点，EA＝FB，AB＝CD.

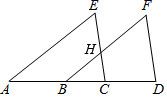(1)、求证：△ACE≌△BDF；

(2)、若CH＝BC，∠A＝50°，求∠D的度数.

查看试题解析
18. 先化简，再求值：
$(\frac{3}{x + 1} - x + 1) \div \frac{x^{2} - 4 x + 4}{x + 1}$ ，从-1，2，-3中选一个值，代入求值.

查看试题解析
19. 如图，平面直角坐标系中A（﹣4，6），B（﹣1，2），C（﹣3，1）．

(1)、作出△ABC关于y轴对称的图形△A₁B₁C₁ ，并写出△A₁B₁C₁各顶点的坐标；

(2)、求△ABC的面积．

查看试题解析
20. 已知 $△ A B C$ 的两边长a和b满足 $\sqrt{a - 9} + (b - 4)^{2} = 0$ .

(1)、若第三边长为c，求c的取值范围.

(2)、若 $△ A B C$ 是等腰三角形，求 $△ A B C$ 的周长.

查看试题解析
21. 探究：我们小学时学过乘法分配律a（b+c）＝ab+ac.

下面我们用等积法证明乘法分配律：

如图，方法一：长方形ABCD的一边长为a，另一边长为（b+c），所以长方形ABCD的面积为a（b+c）；

方法二，长方形ABFE的面积为ab，长方形CDEF的面积为ac，所以长方形ABCD的面积为（ab+ac），所以a（b+c）＝ab+ac.

我们把这种用两种不同的方式表示同一图形面积的方法称为等积法.

(1)、应用
请你用等积法，画出图形，并仿照上面的说理方法证明：（a+b）（c+d）＝ac+ad+bc+bd；

(2)、拓展
请直接写出（a+b）（c+d+e）＝.

查看试题解析
22. 要在规定的天数内修筑一段公路，若让甲队单独修筑，则正好在规定天数内按期完成；若让乙队单独修筑，则要比规定天数多8天才完成.现在由乙队单独修筑其中一小段，用去了规定时间的一半，然后甲队接着单独修筑2天，这段公路还有一半未修筑.若让两队共同再修筑2天，能否完成任务？

查看试题解析
23. 如图1，AC=BC，CD=CE，∠ACB=∠DCE=α，AD、BE相交于点M.

(1)、求证：BE=AD；

(2)、直接用含α的式子表示∠AMB的度数为

(3)、当α=90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图2，判断△CPQ的形状，并加以证明.

查看试题解析