广西壮族自治区桂林市灌阳县2021-2022学年八年级上学期期末数学试卷
试卷更新日期:2022-01-27 类型:期末考试
一、单选题
-
1. 在实数0, , 3.14中,无理数是( )A、3.14 B、0 C、 D、都不是2. 当分式的值不存在,则x的值是( )A、x= 2 B、x= 3 C、 D、3. 用不等式表示“x的5倍大于-7”的数量关系是( )A、5x<-7 B、5x>-7 C、x>7 D、7x<54. 下列各式属于最简二次根式的是( )A、 B、 C、 D、5. 以下列各组长度的线段为边,能构成三角形的是( )A、7,3,4 B、5,6,12 C、3,4,5
 D、1,2,3
6. 下列各式从左往右变形正确的是( )A、 B、 C、 D、7. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
D、1,2,3
6. 下列各式从左往右变形正确的是( )A、 B、 C、 D、7. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )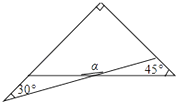 A、165° B、120° C、150° D、135°8. 一个不等式的解集为 , 那么在数轴上表示正确的是( )A、
A、165° B、120° C、150° D、135°8. 一个不等式的解集为 , 那么在数轴上表示正确的是( )A、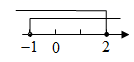 B、
B、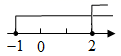 C、
C、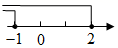 D、
D、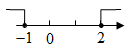 9. 三角形一边上的中线把原三角形分成两个( )A、形状相同的三角形
9. 三角形一边上的中线把原三角形分成两个( )A、形状相同的三角形 B、面积相等的三角形
C、直角三角形
B、面积相等的三角形
C、直角三角形  D、周长相等的三角形
10. 一个正数的两个平方根分别为和 , 则这个正数为( )A、7 B、10 C、 D、10011. 若关于x的一元一次不等式组的解集是 , 则m的取值范围是( )A、 B、 C、 D、12. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC=5,则五边形DECHF的周长为( )
D、周长相等的三角形
10. 一个正数的两个平方根分别为和 , 则这个正数为( )A、7 B、10 C、 D、10011. 若关于x的一元一次不等式组的解集是 , 则m的取值范围是( )A、 B、 C、 D、12. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC=5,则五边形DECHF的周长为( )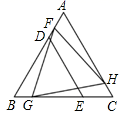 A、8 B、10 C、11 D、12
A、8 B、10 C、11 D、12二、填空题
-
13. 9的算术平方根是 .14. 如果a是b相反数,则+=.15. 2021年,新冠病毒给世界各国带来了极大的灾难,中国在世界抗击新冠病毒疫情中发挥了重要作用.新冠病毒的整体尺寸一般在30~80纳米,请将直径为0.000000052米大的新冠病毒这个数用科学记数法表示为米.16. 命题:“如果m是整数,那么它是有理数”,则它的逆命题为: .17. 某种出租车的收费标准是:起步价7元(即行驶距离不超过3km都需付7元车费),超过3km以后,每增加1㎞,加收2.4元(不足1km按1km计),某人乘这种车从甲地到乙地共支付车费19元,那么,他行程的最大值是.18. 观察下列各式的特点:
① , , , , …;
② , , , , …
计算:++…+
=.
三、解答题
-
19. 计算:.20. 如图,在△ABC中,已知其周长为26㎝.
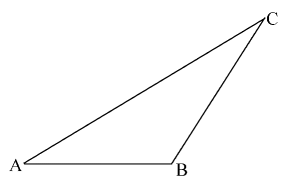 (1)、在△ABC中,用直尺和圆规作边AB的垂直平分线分别交AB、AC于点D,E(不写作法,但须保留作图痕迹).(2)、连接EB,若AD为4㎝,求△BCE的周长.21. 先化简,再求值: ,其中 .22. 解方程: =1﹣ .23. 解不等式组:并把解集在数轴上表示出来.24. 已知,如图,AB=AD,∠B=∠D,∠1=∠2=60°.
(1)、在△ABC中,用直尺和圆规作边AB的垂直平分线分别交AB、AC于点D,E(不写作法,但须保留作图痕迹).(2)、连接EB,若AD为4㎝,求△BCE的周长.21. 先化简,再求值: ,其中 .22. 解方程: =1﹣ .23. 解不等式组:并把解集在数轴上表示出来.24. 已知,如图,AB=AD,∠B=∠D,∠1=∠2=60°.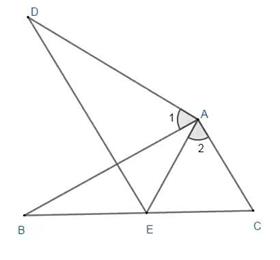 (1)、求证:△ADE≌△ABC;(2)、求证:AE=CE.25. 为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.(1)、求A、B两种学习用品的单价各是多少元?
(1)、求证:△ADE≌△ABC;(2)、求证:AE=CE.25. 为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.(1)、求A、B两种学习用品的单价各是多少元?
(2)、若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
26. 问题发现:(1)、如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,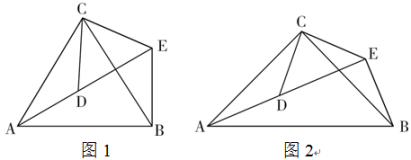
①求证:△ACD≌△BCE;
②求∠AEB的度数.
(2)、拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高交AE于M,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.