1.4 解直角三角形----北师大版九年级下册同步测试
试卷更新日期:2022-01-27 类型:同步测试
一、单选题
-
1. 在 中, ,则 的正弦值为( )A、 B、 C、2 D、2. 如图,在△ABC中,∠C=90°,cosA= ,则sinB=( )
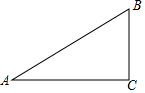 A、 B、 C、 D、3. 如图,在 中, , , ,则 长为( )
A、 B、 C、 D、3. 如图,在 中, , , ,则 长为( )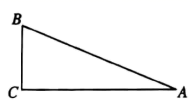 A、 B、 C、 D、4. 如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米.
A、 B、 C、 D、4. 如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米. A、asin40° B、acos40° C、atan40° D、5. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、6. 下表是小红填写的实践活动报告的部分内容:
A、asin40° B、acos40° C、atan40° D、5. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、6. 下表是小红填写的实践活动报告的部分内容:
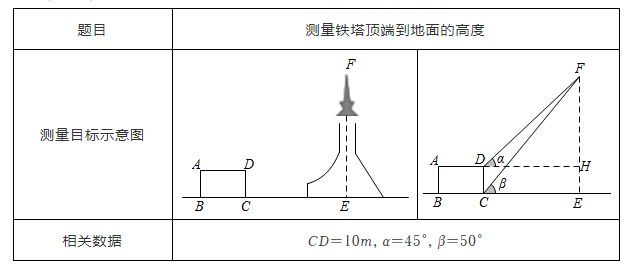
设铁塔顶端到地面的高度 为xm,根据以上条件,可以列出的方程为( )
A、 B、 C、 D、7. 构造几何图形解决代数问题是“数形结合思想”的重要应用,小康在计算 时,构造出如图所示的图形:在Rt ACD中, , ,延长 到 , ,连接 ,得 .根据此图可求得 的结果( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tan∠B的值为 .
 9. 如图,在中,是边上的高, , , , 则的长为 .
9. 如图,在中,是边上的高, , , , 则的长为 . 10. 如图,在平面直角坐标系xOy中,射线OA与x轴正半轴的夹角为α,如果OA= ,tanα=2,那么点A的坐标是 .
10. 如图,在平面直角坐标系xOy中,射线OA与x轴正半轴的夹角为α,如果OA= ,tanα=2,那么点A的坐标是 . 11. 如图1是公园某处的几何造型,如图2是它的示意图,正方形的一部分在水平面 下方,测得 米, ,露出水平面部分的材料长共合计140米(注:共8个大小一样的正方形造型,不计损耗),点 到水平面 的距离为米.
11. 如图1是公园某处的几何造型,如图2是它的示意图,正方形的一部分在水平面 下方,测得 米, ,露出水平面部分的材料长共合计140米(注:共8个大小一样的正方形造型,不计损耗),点 到水平面 的距离为米.
三、解答题
-
12. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.
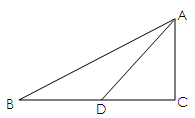 13. 如图,在△ABC中,∠C=90°,∠A=45°,tan∠DBC= ,AB=4 ,求AD的长.
13. 如图,在△ABC中,∠C=90°,∠A=45°,tan∠DBC= ,AB=4 ,求AD的长.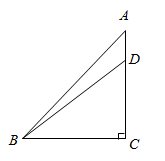 14. 如图,在Rt△ABC中,∠C=90°,BC=2,AC=2 .解这个直角三角形.
14. 如图,在Rt△ABC中,∠C=90°,BC=2,AC=2 .解这个直角三角形.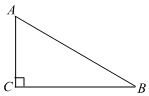 15. 临海大桥主塔是一个轴对称图形(如图所示),小明测得桥面宽度 米, ,求点 到桥面 的距离.(结果精确到0.1米,参考数据: )
15. 临海大桥主塔是一个轴对称图形(如图所示),小明测得桥面宽度 米, ,求点 到桥面 的距离.(结果精确到0.1米,参考数据: )
四、综合题
-
16. 如图1在平面直角坐标系中,O是坐标原点,▱ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G.
 (1)、求∠DCB的度数;(2)、连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF',记直线EF'与射线DC的交点为H.
(1)、求∠DCB的度数;(2)、连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF',记直线EF'与射线DC的交点为H.①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;
②若△EHG的面积为3 ,求点F的坐标.