北京市海淀区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系xOy中，下列函数的图象经过点 $(0 ， 0)$ 的是（）

A、 $y = x + 1$ B、 $y = x^{2}$ C、 $y = (x - 4)^{2}$ D、 $y = \frac{1}{x}$

查看试题解析
2. 下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 抛物线 $y = (x - 2)^{2} + 1$ 的顶点坐标是（）

A、 $(2 ， 1)$ B、 $(1 ， 2)$ C、 $(- 2 ， 1)$ D、 $(1 ， - 2)$

查看试题解析
4. 在△ABC中， $C A = C B$ ，点O为AB中点．以点C为圆心，CO长为半径作⊙C，则⊙C 与AB的位置关系是（）

A、相交 B、相切 C、相离 D、不确定

查看试题解析
5. 小明将图案绕某点连续旋转若干次，每次旋转相同角度 $α$ ，设计出一个外轮廓为正六边形的图案（如图），则 $α$ 可以为（）

A、30° B、60° C、90° D、120°

查看试题解析
6. 把长为2 m的绳子分成两段，使较长一段的长的平方等于较短一段的长与原绳长的积．设较长一段的长为x m，依题意，可列方程为（）

A、 $x^{2} = 2 (2 - x)$ B、 $x^{2} = 2 (2 + x)$ C、 $(2 - x)^{2} = 2 x$ D、 $x^{2} = 2 - x$

查看试题解析
7. 如图，A，B，C是某社区的三栋楼，若在AC中点D处建一个5G基站，其覆盖半径为300 m，则这三栋楼中在该5G基站覆盖范围内的是（）

A、A，B，C都不在 B、只有B C、只有A，C D、A，B，C

查看试题解析
8. 做随机抛掷一枚纪念币的试验，得到的结果如下表所示：
抛掷次数m
500
1000
1500
2000
2500
3000
4000
5000
“正面向上”的次数n
265
512
793
1034
1306
1558
2083
2598
“正面向上”的频率 $\frac{n}{m}$
0.530
0.512
0.529
0.517
0.522
0.519
0.521
0.520
下面有3个推断：
①当抛掷次数是1000时，“正面向上”的频率是0.512，所以“正面向上”的概率是0.512；
②随着试验次数的增加，“正面向上”的频率总在0.520附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.520；
③若再次做随机抛掷该纪念币的实验，则当抛掷次数为3000时，出现“正面向上”的次数不一定是1558次．其中所有合理推断的序号是（）

A、② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

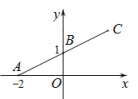
9. 已知某函数当 $x > 0$ 时，y随x的增大而减小，则这个函数解析式可以为．

查看试题解析
10. 在一个不透明袋子中有3个红球和2个黑球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则取出红球的概率是．

查看试题解析
11. 若点 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ 在抛物线 $y = 2 x^{2}$ 上，则 $y_{1}$ ， $y_{2}$ 的大小关系为： $y_{1}$ $y_{2}$ （填“＞”，“=”或“＜”）．

查看试题解析
12. 如图，在平面直角坐标系xOy中，点 $A$ $（ - 2 ， 0 ）$ ，点 $B$ $（ 0 ， 1 ）$ ．将线段BA绕点B旋转180°得到线段BC，则点C的坐标为．

查看试题解析
13. 若关于x的一元二次方程 $x^{2} - 2 x + k = 0$ 有两个不相等的实数根，则k 的取值范围是.

查看试题解析
14. 如图，PA，PB分别切⊙O于点A，B，Q是优弧 $\overset{⌢}{A B}$ 上一点，若∠P=40°，则∠Q的度数是．

查看试题解析
15. 小明烘焙了几款不同口味的饼干，分别装在同款的圆柱形盒子中．为区别口味，他打算制作“** 饼干”字样的矩形标签粘贴在盒子侧面．为了获得较好的视觉效果，粘贴后标签上边缘所在弧所对的圆心角为90°（如图）．已知该款圆柱形盒子底面半径为6 cm，则标签长度l应为 cm．（π取3.1）

查看试题解析
16. 给定二元数对（p，q），其中 $p = 0$ 或1， $q = 0$ 或1．三种转换器A，B，C对（p，q）的转换规则如下：

(1)、在图1所示的“A—B—C”组合转换器中，若输入 $(1 ， 0)$ ，则输出结果为；

(2)、在图2所示的“①—C—②”组合转换器中，若当输入 $(1 ， 1)$ 和 $(0 ， 0)$ 时，输出结果均为0，则该组合转换器为“—C—”（写出一种组合即可）．

查看试题解析
17. “化圆为方”是古希腊尺规作图难题之一，即：求作一个正方形，使其面积等于给定圆的面积．这个问题困扰了人类上千年，直到19世纪，该问题被证明仅用直尺和圆规是无法完成的．如果借用一个圆形纸片，我们就可以化圆为方，方法如下：
已知：⊙O（纸片），其半径为 $r$ ．
求作：一个正方形，使其面积等于⊙O的面积．
作法：①如图1，取⊙O的直径 $A B$ ，作射线 $B A$ ，过点A作 $A B$ 的垂线l；
②如图2，以点A为圆心， $O A$ 为半径画弧交直线l于点C；
③将纸片⊙O沿着直线l向右无滑动地滚动半周，使点A，B分别落在对应的 $A$ ， $B$ 处；
④取 $C B$ 的中点M，以点M为圆心， $M C$ 为半径画半圆，交射线 $B A$ 于点E；
⑤以 $A E$ 为边作正方形 $A E F G$ ．
正方形 $A E F G$ 即为所求．
根据上述作图步骤，完成下列填空：

(1)、由①可知，直线l为⊙O的切线，其依据是．

(2)、由②③可知， $A C = r$ ， $A B = π r$ ，则 $M C =$ ， $M A =$ （用含r的代数式表示）．

(3)、连接 $M E$ ，在Rt $△ A M E$ 中，根据 $A M^{2} + A E^{2} = E M^{2}$ ，可计算得 $A E^{2} =$ （用含r的代数式表示）．由此可得 $S_{正方形 A E F G} = S_{⊙ o}$ ．

查看试题解析

三、解答题

18. 解方程： $x^{2} - 6 x + 8 = 0$

查看试题解析
19. 已知a是方程 $2 x^{2} - 7 x - 1 = 0$ 的一个根，求代数式 $a (2 a - 7) + 5$ 的值．

查看试题解析
20. 在平面直角坐标系xOy中，抛物线 $y = a (x - 3)^{2} - 1$ 经过点 $(2 ， 1)$ ．

(1)、求该抛物线的表达式；

(2)、将该抛物线向上平移个单位后，所得抛物线与x轴只有一个公共点．

查看试题解析
21. 如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，将线段CA绕点C逆时针旋转60°，得到线段CD，连接AD，BD．

(1)、依题意补全图形；

(2)、若BC=1，求线段BD的长．

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} + (2 - m) x + 1 - m = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、若 $m < 0$ ，且此方程的两个实数根的差为3，求m的值．

查看试题解析
23. 如图，△ABC内接于⊙O，高AD经过圆心O．

(1)、求证： $A B = A C$ ；

(2)、若 $B C = 8$ ， ⊙O的半径为5，求△ABC的面积．

查看试题解析
24. 邮票素有“国家名片”之称，方寸之间，包罗万象．为宣传2022年北京冬奥会，中国邮政发行了一套冬奥会邮票，其中有一组展现雪上运动的邮票，如图所示：
某班级举行冬奥会有奖问答活动，答对的同学可以随机抽取邮票作为奖品．

(1)、在抢答环节中，若答对一题，可从4枚邮票中任意抽取1枚作为奖品，则恰好抽到“冬季两项”的概率是；

(2)、在抢答环节中，若答对两题，可从4枚邮票中任意抽取2枚作为奖品，请用列表或画树状图的方法，求恰好抽到“高山滑雪”和“自由式滑雪”的概率．

查看试题解析
25. 如图，AB为⊙O的直径，弦 $C D ⊥ A B$ 于E，连接 $A C$ ，过A作 $A F ⊥ A C$ ，交⊙O于点F，连接DF，过B作 $B G ⊥ D F$ ，交DF的延长线于点G．

(1)、求证：BG是⊙O的切线；

(2)、若 $∠ D F A = 30 °$ ， DF=4，求FG的长．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，点 $(4 ， 3)$ 在抛物线 $y = a x^{2} + b x + 3 (a > 0)$ 上．

(1)、求该抛物线的对称轴；

(2)、已知 $m > 0$ ，当 $2 - m \leq x \leq 2 + 2 m$ 时，y的取值范围是 $- 1 \leq y \leq 3$ ，求a，m的值；

(3)、在（2）的条件下，是否存在实数n，当 $n - 2 < x < n$ 时，y的取值范围是 $3 n - 3 < y < 3 n + 5$ ，若存在，直接写出n的值；若不存在，请说明理由．

查看试题解析
27. 如图，在△ABC中， $∠ B A C = 90 °$ ， $A B = A C = 1$ ，延长CB，并将射线CB绕点C逆时针旋转90°得到射线l，D为射线l上一动点，点E在线段CB的延长线上，且 $B E = C D$ ，连接DE，过点A作 $A M ⊥ D E$ 于M．

(1)、依题意补全图1，并用等式表示线段DM与ME之间的数量关系，并证明；

(2)、取BE的中点N，连接AN，添加一个条件：CD的长为，使得 $A N = \frac{1}{2} D E$ 成立，并证明．

查看试题解析
28. 在平面直角坐标系xOy中，图形W上任意两点间的距离有最大值，将这个最大值记为d．对点P及图形W给出如下定义：点Q为图形W上任意一点，若P，Q两点间的距离有最大值，且最大值恰好为2d，则称点P为图形W的“倍点”．

(1)、如图1，图形W是半径为1的⊙O．
①图形W上任意两点间的距离的最大值d为；
②在点 $P_{1}$ （0，2）， $P_{2}$ （3，3）， $P_{3}$ （ $- 3$ ， 0）中，⊙O的“倍点”是；

(2)、如图2，图形W是中心在原点的正方形ABCD，已知点A（-1，1），若点E（t，3）是正方形ABCD的“倍点”，求t的值；

(3)、图形W是长为2的线段MN，T为MN的中点，若在半径为6的⊙O上存在MN的“倍点”，直接写出满足条件的点T所构成的图形的面积．

查看试题解析

抛掷次数m	500	1000	1500	2000	2500	3000	4000	5000
“正面向上”的次数n	265	512	793	1034	1306	1558	2083	2598
“正面向上”的频率 $\frac{n}{m}$	0.530	0.512	0.529	0.517	0.522	0.519	0.521	0.520